MathOptimizer Professional

Advanced Global and Local Nonlinear Optimization Using the External LGO Solver Suite

MathOptimizer Professional combines the power of Mathematica with the established LGO (Lipschitz Global Optimizer) solver suite, offering sophisticated application development tools and a solver-based functionality comparable to other compiler-based or optimization modeling language-related implementations.

In use since 1990, the LGO solver engine is currently available for professional C and Fortran compiler platforms, with links to Excel and several prominent optimization modeling languages.

MathOptimizer Professional enables the global and local solution of a general class of continuous optimization problems. The model form considered is:

min f(x)  subject to  xDRⁿ  D:={x: xlxxu  g(x)0}

Here xRn is the vector of decision variables (Rn denotes the Euclidean real n-space); f:RnR1 is a continuous objective function; DRn is the nonempty set of feasible decisions defined by explicit, finite (with respect to components) lower and upper bounds xl and xu and by a collection of continuous constraint functions g:RnRm. (Obviously, g(x)0 formally covers all cases of g(x)~0, where ~ denotes any of the operators =, and .)

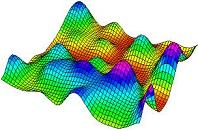
These key analytical assumptions guarantee that the model considered has a globally optimal solution. At the same time--without further specific structural assumptions--this model can represent a very difficult numerical challenge because of the possibility of having a disconnected, nonconvex, feasible region and a multitude of local optima. For illustration, please see the graphic above, which shows the squared error function related to solving a given pair of transcendental equations as a function of the two unknown arguments.

MathOptimizer Professional automatically transforms optimization models formulated in Mathematica into C or Fortran code, then the coded model is handed over to the LGO to be solved. Following a seamless optimization model compilation/linking/execution procedure, the optimization results are directly returned to the calling Mathematica file. This approach can lead to significant program execution speedup, which becomes more noticeable with increasing model sizes. MathOptimizer Professional can be used to handle models with thousands of decision variables and general constraints; algorithmic advances and more powerful computers will enable the handling of even larger models.

More information is available on the features page and from the list of references.

About the Developer

MathOptimizer Professional is developed and supported by János D. Pintér.

János D. Pintér, PhD, DSc, is a researcher and software developer working mostly in the area of nonlinear optimization. He received the 2000 INFORMS Computing Society Prize for his book Global Optimization in Action. He has authored and edited several other books and about 200 other publications related to systems modeling and optimization. Dr. Pintér has served on the editorial board of the Journal of Global Optimization since its 1991 founding, and of the book series SpringerBriefs in Optimization. He is the principal developer of a range of optimization software packages. Dr. Pintér offers consulting services, lectures and training courses focused on computational nonlinear optimization.

János D. Pintér, PhD, DSc
janos.d.pinter@gmail.com

MathOptimizer Professional is available for Windows and requires Mathematica 10 or greater and a C or Fortran compiler (specify compiler at time of purchase). Please contact the developer for other platforms; for MathOptimizer Professional implementations for use with other C and Fortran compilers not listed; and for additional model development, customization and test services.