More than three decades ago, we revolutionized maths and its applications with Mathematica But that was just the beginning…
Ever since, we've been energetically building the vast and singular system that now delivers the transformative power of our unified approach to computation to everything — from research, development and education to deployment and more…
STEM

Healthcare

Sustainable
Energy
Energy

Political
Science
Science

FinTech

Business
Analysis
Analysis

Manufacturing

Computational
Philosophy
Philosophy

Cognitive
Science
Science

Computer
Security
Security

Publishing

Computational
Journalism
Journalism

Content
Generation
Generation

Marketing
Science
Science

Retail

Real
Estate
Estate

Plant
Science
Science

Acoustics

AgTech

Astronomy

Civil
Engineering
Engineering

Ecology

Transportation

Architecture

CAD

Media
Analysis
Analysis

AdTech

Computer
Vision
Vision

Computational
Music
Music

Applied
Maths
Maths

Mathematics

Cryptography

Lab
Automation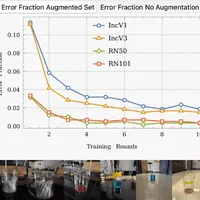
Automation

Software
Engineering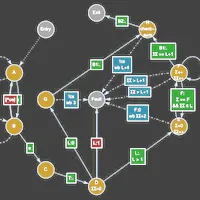
Engineering

Biostatistics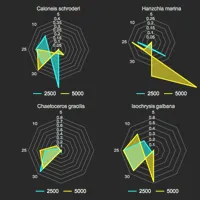

Experimental
Analysis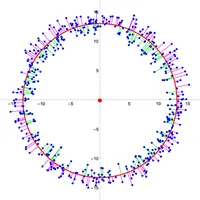
Analysis

Urban
Studies
Studies

Food
Science
Science

Chemical
Engineering
Engineering

Archaeology

Utilities

Network
Science
Science

Risk
Analysis
Analysis

Statistics

Management
Science
Science

Economics

Industrial
Engineering
Engineering

Optics

Planetary
Science
Science

Electrical
Engineering
Engineering

IoT

Mining

Insurance

System
Design
Design

Remote
Sensing
Sensing

Computer
Science
Science

Computer
Engineering
Engineering

Systems
Analysis
Analysis

Earth
Science
Science

Forensic
Science
Science

Environmental
Engineering
Engineering

Natural
Resources
Resources

Information
Science
Science

Life
Sciences
Sciences

Environmental
Science
Science

Sports
Analytics
Analytics

Blockchain

GameTech

Neuroscience

Pharmacology

Computational
Biology
Biology

Bioengineering

EdTech

Quantum Computing

Complexity
Science
Science

Ruliology

Creative
Arts
Arts

Computational
Humanities
Humanities

Linguistics

Art
History
History

Public
Health
Health

Logistics

Production
Engineering
Engineering

Energy
Modeling
Modeling

Material
Science
Science

Psychology

Aerospace
& Defense
& Defense

Robotics

Operations
Research
Research

Automotive
Engineering
Engineering

Experimental
Analysis
Analysis

So many inventions… so many discoveries…
so many academic achievements…
so many systems deployed…
Delivering the tools of choice for the world's intellectual leaders
- Personal
The unique power of our system comes from its elegant unification of an immense range of capabilities, algorithms, models and data into the breakthrough Wolfram Language — transcending programming to provide a full computational representation of the world
Integrated Capabilities of the Wolfram System
- Device Connectivity
- Sequence Analysis
- Symbolic Programming
- Polynomial Computation
- Mathematical Functions
- Signal Processing
- Random Processes
- Audio Analysis
- Finite Element Analysis
- Scheduled Tasks
- Automated Theorem Proving
- Reliability Analysis
- Earth Science Data
- Historical Data
- System Modeling
- Parallel Computation
- Synthetic Geometry
- Astronomical Computation
- Actuarial Computation
- Computational Chemistry
- Geographic Data
- Instant API Generation
- Graph Theory
- Information Visualization
- Tensor Manipulation
- Cultural & Linguistic Data
- Boolean Computation
- Algebraic Manipulation
- AR/VR/XR
- Foreign Function Interface
- Symbolic Calculus
- C++/Python Connectivity
- Array Manipulation
- Computational Geometry
- GPU Computing
- Speech Processing
- Group Theory
- Meteorological Data
- Probability Theory
- Physical Science Data
- Function Visualization
- Functional Programming
- Statistical Analysis
- Natural Language Processing
- Discrete Calculus
- Data Visualization
- Equation Solving
- Web Programming
- Convex Optimization
- Semantic Search & RAG
- Video Analysis
- Machine Learning
- Knowledge Representation
- Discrete Maths
- Cartography
- 3D Geometry & Printing
- Cloud Deployment
- Symbolic Computation
- Sound Generation
- Complex Analysis
- Image Processing
- Notebook Programming
- Boolean Algebra
- Numerical Computation
- Matrix Computation
- LLM Programming
- Financial Computation
- Differential Equations
- Ruliology
- String Manipulation
- Number Theory
- Units & Measures
- Mathematical Typesetting
- Neural Networks
- Pattern Matching
- Blockchain
- Dynamic Visualization
- Video Generation
- Geographic Visualization
- Geodetic Computation
- List Manipulation
- Control Theory
- Arbitrary-Precision Computation
- Database Connectivity
- Symbolic Graphics
- Game Theory
- Text Analysis
- Cryptography
- Curated API Connectivity
- Molecular Visualization
- Computer Vision
- Chemical Data
- User Interface Construction
- Socioeconomic Data
- Dynamical Systems Theory
- Food & Nutrition Data
- Bioinformatics
- Report Generation
- Time Series
Turn your ideas into computational reality with Wolfram Language
Use it directly as a tool of thought — or build systems of any scale with it  (or let us build them for you)
(or let us build them for you)
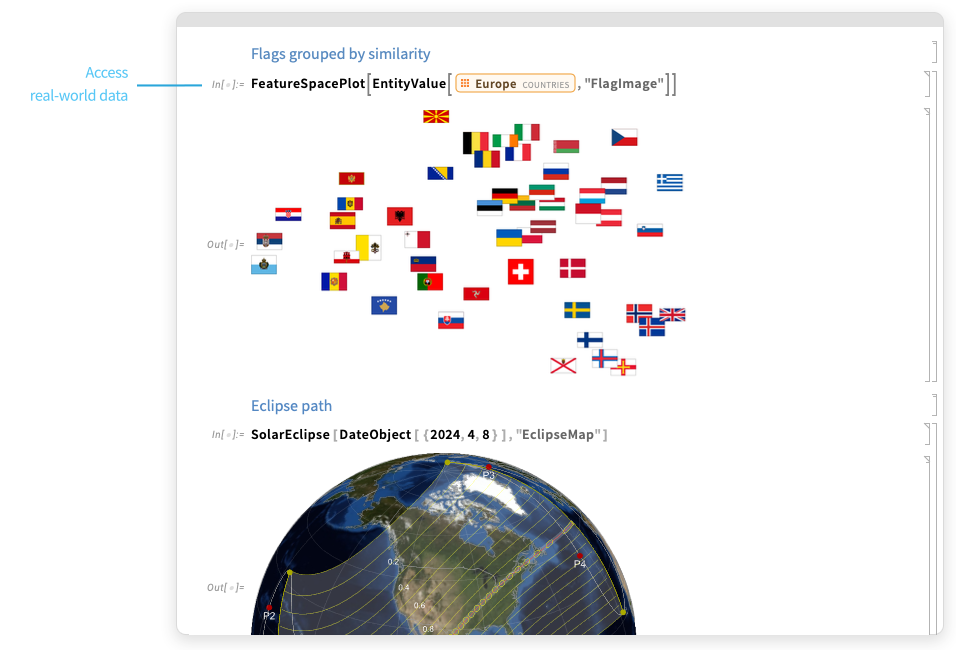
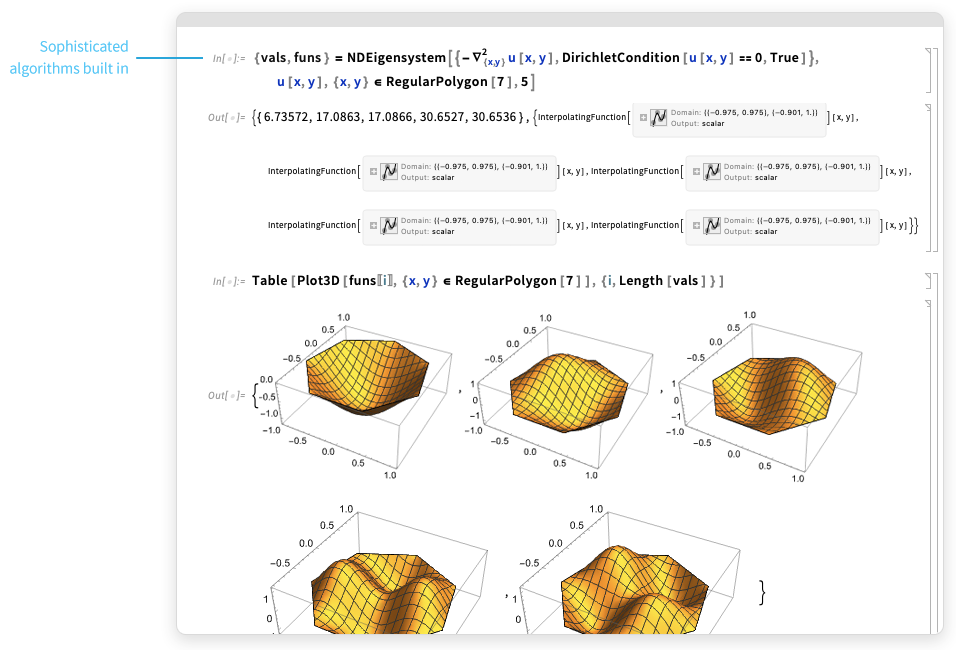
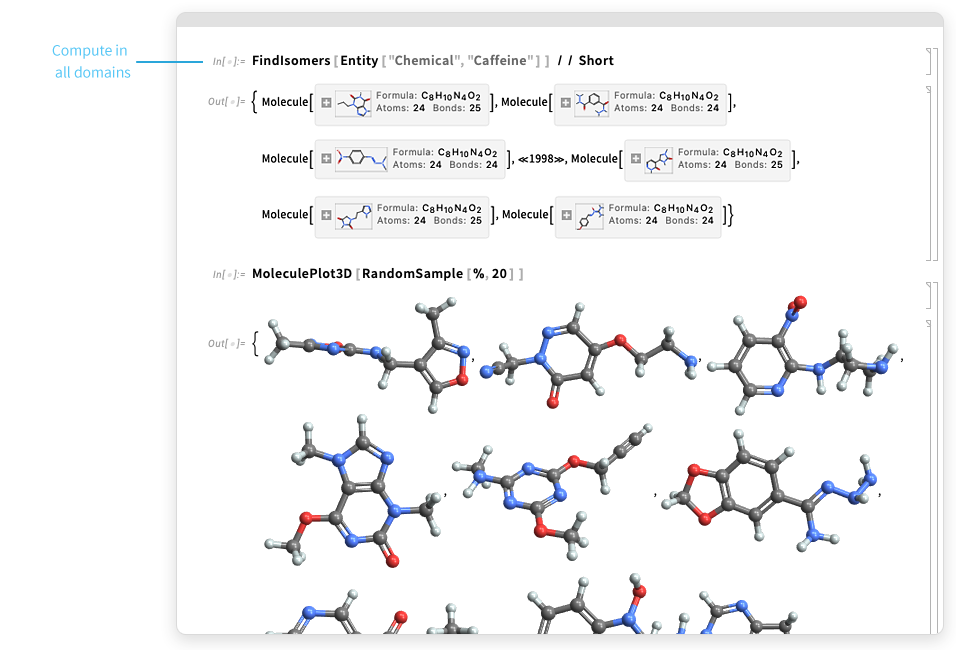
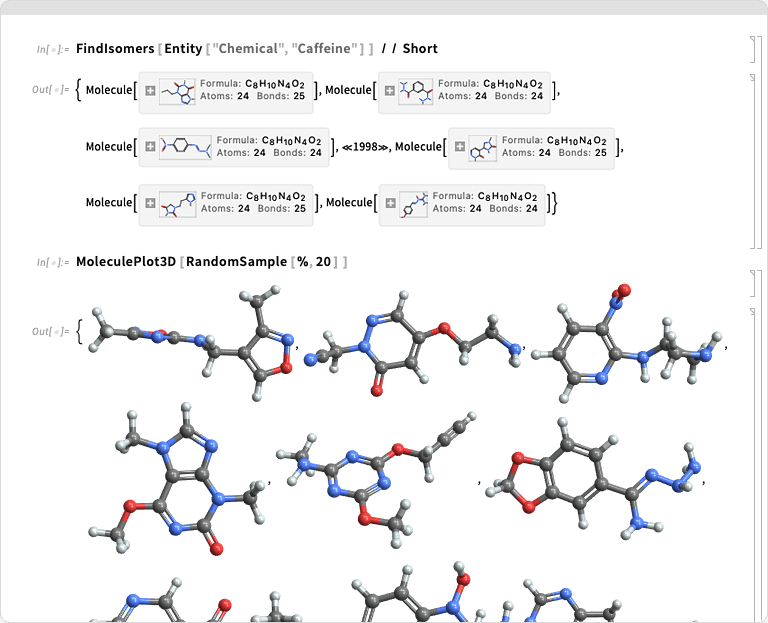
Compute. Develop.Deploy everywhere...
Interactive Web Apps
Standalone Apps
User Interfaces
Desktop Notebooks
Web Notebooks
Mobile
AR/VR/XR
3D Printouts
Presentations
Generated Reports
Dashboards
Form Pages
Interactive Documents
Computational Essays
Academic Papers
Educational Assessments
Visualizations
APIs
External Languages
Code Generation
Embedded Systems
Blockchain
Cloud Providers
Private Cloud
Use the power of Wolfram to supercharge your organization, your career or your education!
Get Wolfram Now
Contact Wolfram Sales
Request a corporate demo
Used Wolfram or Mathematica before? Find out what's new
Instant Resources
Wolfram|Alpha
Providing expert-level computation and knowledge to everyoneWolfram Demonstrations
13,000+ interactive explorations for education, research, recreation and moreWolfram U
Learning resources for the computational universeDeveloper Resources
Deployment
- Big Picture
- Learn Our Tech
- For Students
- Wolfram Channels