Aujourd'hui, plus que jamais, le calcul financier ne se limite pas à la simple compilation de chiffres, et les nouveaux dirigeants financiers se tournent vers Mathematica pour obtenir de l'aide.

Les sociétés d'investissement « découpent » régulièrement des titres tels que des hypothèques, des obligations d'État et même des obligations de pacotille pour atteindre des objectifs spécifiques en matière de risque et de rendement. Si les tableurs et C/C++ restent utiles, les langages de programmation symboliques (c'est-à-dire les langages qui manipulent à la fois les chiffres et les symboles qui représentent les structures financières) sont de plus en plus nécessaires pour faire face à la complexité croissante du monde financier.

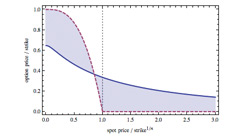
Dr Ross Miller¹, l'un des premiers à avoir adopté une approche symbolique de l'analyse financière, a utilisé Mathematica pour créer un modèle relativement simple qui est traditionnellement de nature numérique : le modèle d'évaluation des options de Black-Scholes.

« Mathematica permet de manipuler la formule d'évaluation de Black-Scholes directement en tant qu'entité symbolique. Cela simplifie grandement le calcul des différentes caractéristiques de risque d'une option (une tâche qui est à la fois fastidieuse et sujette à des erreurs lorsqu'elle est effectuée de manière plus traditionnelle) et facilite les extensions du modèle qui sont faites "à la volée". »

Mathematica a ensuite permis de reprendre le modèle d'évaluation des options de Black-Scholes là où il s'était arrêté. Bien que le modèle de Black-Scholes donne une solution fermée pour l'évaluation des options européennes, de nombreuses autres options ne peuvent pas être évaluées par ce modèle. Il s'agit notamment des options américaines et des options dont les gains finaux dépendent de la trajectoire suivie par le cours de l'action. En utilisant les modèles d'évaluation des options binaires et binomiales et la méthode de Monte Carlo, trois ingénieurs financiers² ont utilisé Mathematica pour évaluer de telles options.

« Sans Mathematica, d'autres personnes ont dû utiliser des approximations de formules de tarification pour des options difficiles à tarifer. Mathematica nous a permis de fixer directement le prix d'un grand nombre de ces options. »

1. Dr Ross Miller est l'auteur du livre Computer-Aided Financial Analysis et a publié plusieurs articles sur le transfert d'informations sur les marchés financiers et sur la conception de systèmes de marché électroniques avancés. Il a été responsable de la recherche à la National Westminster Bank et a fait partie du personnel technique du General Electric Corporate Research and Development Center avant de créer sa propre société de conseil spécialisée dans la gestion des investissements et des risques.

2. Simon Benninga, Raz Steinmetz et John Stroughair. Dr Benninga est l'auteur de Numerical Methods in Finance. Ses recherches portent notamment sur les marchés des options et des contrats à terme. Raz Steinmetz et John Stroughair étaient étudiants à la Wharton School de la University of Pennsylvania lorsque cette recherche a été menée.