Mathematica aide à découvrir le plus grand nombre premier connu

« Mathematica est un environnement idéal pour le mélange nécessaire de symboles et de chiffres et pour le type d'exploration interactive qui conduit à un algorithme nouveau et non standard. »

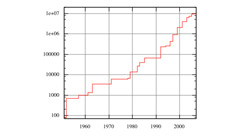
En juin 1999, un groupe international de mathématiciens, d'informaticiens et d'amateurs, réunis sous la bannière du Great Internet Mersenne Prime Search (GIMPS), a découvert que 2^6972593-1 est un nombre premier. Ce nombre est actuellement le plus grand nombre premier connu. Les découvreurs sont officiellement N. Hajratwala, G. Woltman et S. Kurowski, le premier étant le bénévole dont la machine a trouvé le nombre premier et les derniers étant les architectes du logiciel/réseau. Ce nombre premier est long de 2 098 960 chiffres décimaux et peut donc prétendre à un prix de 50 000 dollars de la part de l'Electronic Frontier Foundation. Il est intéressant de noter qu'au début des années 1990, Mathematica a joué un rôle important dans la réalisation de cette découverte.

Tout d'abord, une perspective historique : les nombres premiers de la forme 2^q-1 sont appelés « nombres premiers de Mersenne » d'après le moine français Marin Mersenne (1588-1648), qui en a discuté dans sa correspondance avec le grand Fermat. Les nombres premiers de Mersenne jouent depuis longtemps un rôle important dans la théorie des nombres, par exemple dans la théorie des nombres dits parfaits et dans la cryptographie, où certains champs algébriques bénéficient d'une arithmétique efficace basée sur les nombres de Mersenne. Bien que les nombres premiers de Mersenne soient étudiés depuis des siècles, de nombreuses questions fondamentales demeurent, notamment celle de savoir s'il en existe un nombre infini.

Le seul moyen de déterminer si un très grand nombre est réellement premier est d'effectuer un test de primalité qui, dans le cas des nombres premiers de Mersenne, peut être une manifestation efficace appelée test de Lucas-Lehmer. Le test de Lucas-Lehmer consiste à élever au carré des nombres géants, des nombres comportant des milliers ou des millions de chiffres.

Pour ce type d'arithmétique, l'algorithme sous-jacent, une « transformation pondérée discrète à base irrationnelle » (IBDWT), a été développé au début des années 1990 par R. Crandall au Reed College et NeXT, Inc. en utilisant Mathematica comme environnement de prototypage. C'est cet algorithme que Woltman a coulé au milieu des années 1990 sous forme de variante assembleur, complétant ainsi le cycle de prototypage/développement pour lequel Mathematica est idéal.

L'idée de l'IBDWT est de développer des nombres géants dans une base irrationnelle. On applique ensuite une transformée discrète pondérée, une variante de la FFT classique, pour multiplier ou élever au carré des nombres dans cette base avec une rapidité sans précédent. « Mathematica est un environnement idéal pour le mélange nécessaire de symboles et de chiffres et pour le type d'exploration interactive qui conduit à un algorithme nouveau et non standard, » comme l'explique Crandall.

Un poster mural des nombres premiers, montrant tous les chiffres décimaux (plus de deux millions) du nombre premier record, est disponible auprès de Perfectly Scientific, Inc.