Wolfram Language™

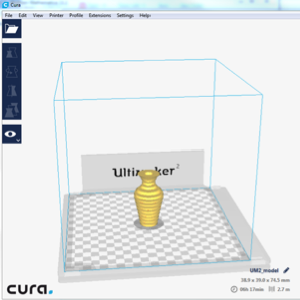
Die optimale Ausrichtung für den 3D-Druck finden

Dank der umfassenden Unterstützung für gitternetzbasierte geometrische Regionen lassen sich Druckbarkeitsanalysen von der Berechnung der statischen Belastung bis hin zur Durchführbarkeit einer aufrechten Ausrichtung ganz einfach ausführen.

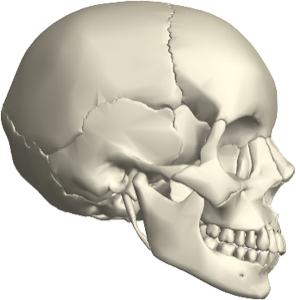
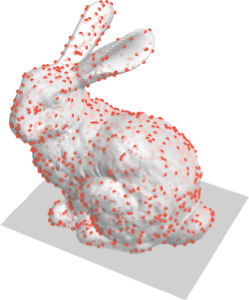
Ermitteln Sie mögliche Ausrichtungen des Modells, wie es auf einem ebenen Untergrund platziert werden kann.

In[1]:=

cover = TransformedRegion[ MeshRegion[ Import["http://www.thingiverse.com/download:342676", "STL"], PlotTheme -> "Minimal"], TransformationFunction[{{1., 0.5, 0.03, -0.06}, {-0.05, 0.03, 1.1, 0.1}, {0.53, -1.02, 0.05, 0.19}, {0, 0, 0, 1.}}]]; points = MeshCoordinates[cover]; transform[Polygon[points_]] := Module[{proj = points}, proj[[All, 3]] = 0; Last[FindGeometricTransform[proj, points]]]; highlight[convexHull_, cover_] := Show[HighlightMesh[ convexHull, {Style[1, Brown], Style[2, Opacity[0.3, Brown]]}], cover]; Show[cover, Boxed -> True]

Out[1]=

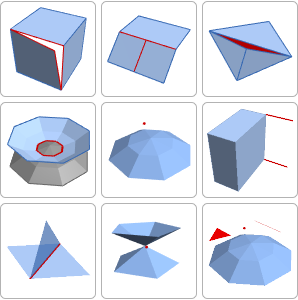
Jede Seite der konvexen Hülle kann die Unterseite einer möglichen Ausrichtung sein.

In[2]:=

convexHull = ConvexHullMesh[points]; orientations = MeshPrimitives[convexHull, 2]; highlight[convexHull, cover]

Out[2]=

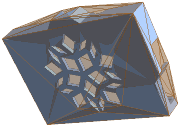
Verwenden Sie die Orthogonalprojektion des Schwerpunkts, um die möglichen Ausrichtungen weiter einzuschränken.

In[3]:=

masscenter = RegionCentroid[cover]; projection[polygon_, p_] := RegionNearest[AffineSpace @@ polygon, p]; candidates = Select[orientations, RegionMember[#, projection[#, masscenter]] &];

Eine mögliche Ausrichtung.

In[4]:=

Show[ncover = TransformedRegion[cover, transform[Last[SortBy[candidates, Area]]]], Boxed -> True]

Out[4]=

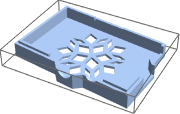
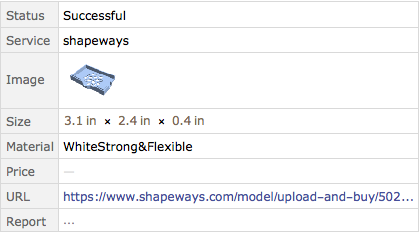
Drucken Sie das Modell.

In[5]:=

Printout3D[ncover, "Shapeways"]

Out[5]=