Automatic Region Simplification
Operations on special regions are improved in Version 11 to give the best representations in terms of special regions where possible.
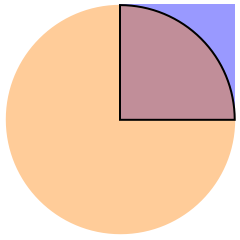
Intersect the unit disk with the unit rectangle.
In[1]:=
RegionIntersection[Disk[], Rectangle[]]Out[1]=
Apply an affine transformation to a special region.
In[2]:=
TransformedRegion[Disk[{1, 2}, {1, 2}],
AffineTransform[{{{1, 2}, {3, 1}}, {1, 2}}]]Out[2]=
In[3]:=
TransformedRegion[Rectangle[],
ShearingTransform[\[Pi]/4, {1, 0}, {0, 1}]]Out[3]=
Take the product of two regions and produce a special region of higher dimension.
In[4]:=
RegionProduct[Interval[{a, b}], Disk[{x, y}, r]]Out[4]=
In[5]:=
RegionProduct[Parallelepiped[{1, 1, 1}, IdentityMatrix[3]],
Rectangle[]]Out[5]=
Compute the difference between special regions.
In[6]:=
RegionDifference[Disk[{0, 0}, 2], Rectangle[{2, 2}]]Out[6]=
In[7]:=
RegionDifference[Cuboid[], Ball[{0, 0, 0}, 2]]Out[7]=