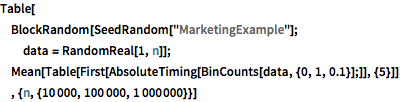データビニングのパフォーマンスの向上

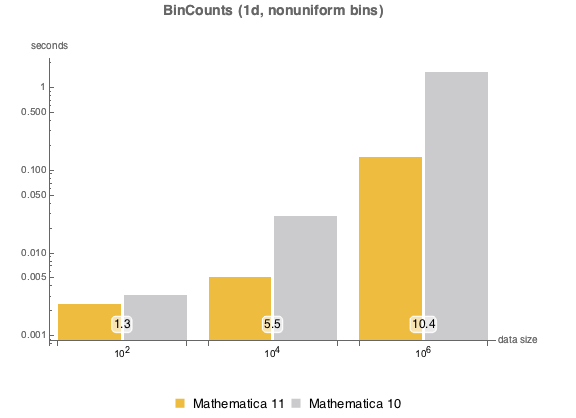
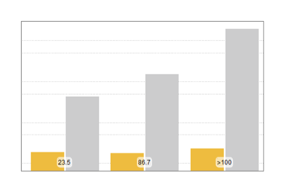
データビニングにかかる時間を比べる．以下のグラフは，さまざまなサンプルサイズとビン指定について速度を比較したものである．実験は，Intel Xeon Processor E3-1245 v2 3.40 GHzを搭載したWindows 10のシステムを使って行われた．一番下の数字は，バージョン11がバージョン10と比べてどのくらい速いかを示す．

非一様な一次元のビン．

In[1]:=

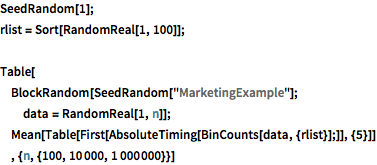
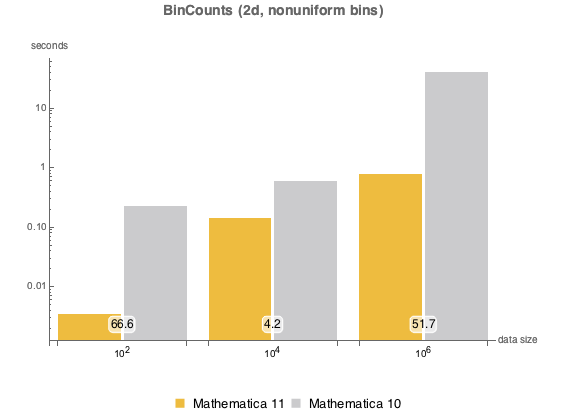
SeedRandom[1]; rlist = Sort[RandomReal[1, 100]]; Table[ BlockRandom[SeedRandom["MarketingExample"]; data = RandomReal[1, n]]; Mean[Table[First[AbsoluteTiming[BinCounts[data, {rlist}];]], {5}]] , {n, {100, 10000, 1000000}}]

Out[139]=

非一様な二次元のビン．

In[2]:=

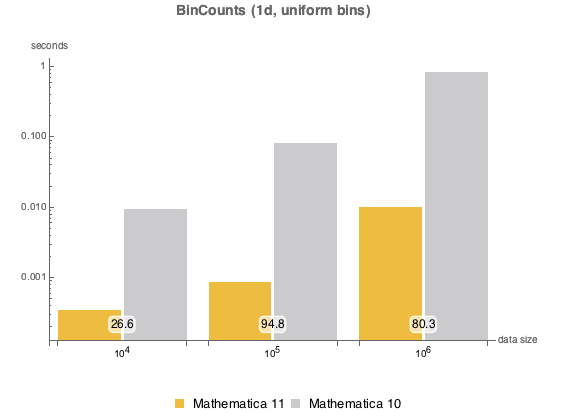
SeedRandom[1]; rlist1 = Sort[RandomReal[1, 100]]; rlist2 = Sort[RandomReal[1, 100]]; Table[ BlockRandom[SeedRandom["MarketingExample"]; data = RandomReal[1, {n, 2}]]; Mean[Table[ First[AbsoluteTiming[BinCounts[data, {rlist1}, {rlist2}];]], {5}]] , {n, {100, 10000, 1000000}}]

Out[141]=

一様な一次元のビン．

In[3]:=

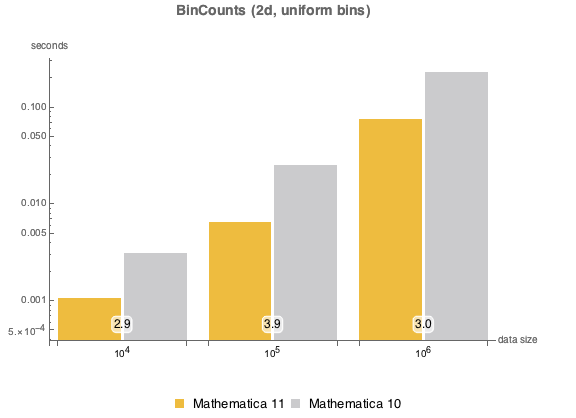
Table[ BlockRandom[SeedRandom["MarketingExample"]; data = RandomReal[1, n]]; Mean[Table[First[AbsoluteTiming[BinCounts[data, {0, 1, 0.1}];]], {5}]] , {n, {10000, 100000, 1000000}}]

Out[143]=

一様な二次元のビン．

In[4]:=

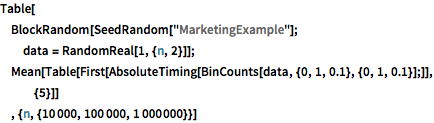
Table[ BlockRandom[SeedRandom["MarketingExample"]; data = RandomReal[1, {n, 2}]]; Mean[Table[ First[AbsoluteTiming[ BinCounts[data, {0, 1, 0.1}, {0, 1, 0.1}];]], {5}]] , {n, {10000, 100000, 1000000}}]

Out[145]=