Multivariate Normality Test

BaringhausHenzeTest is a multivariate normality test with the test statistic based on the empirical characteristic function. It is also known as the Baringhaus–Henze–Epps–Pulley (BHEP) test.

In[1]:=

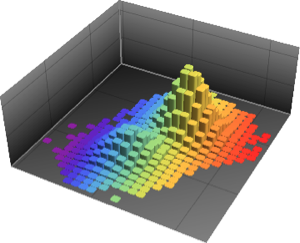
data = RandomVariate[NormalDistribution[], {10^3, 3}];

In[2]:=

BaringhausHenzeTest[data]

Out[2]=

The test statistic is invariant under affine transformations of the data.

In[3]:=

data2 = AffineTransform[{RandomReal[1, {3, 3}], RandomReal[1, 3]}][ data]; {BaringhausHenzeTest[data2, "TestStatistic"], BaringhausHenzeTest[data, "TestStatistic"]}

Out[3]=

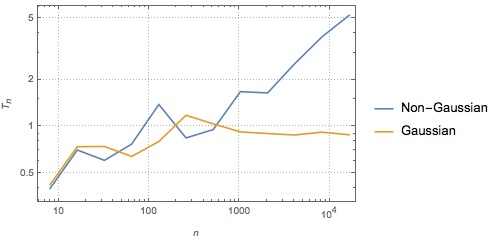
The test statistic is also consistent against every alternative distribution—that is, it grows unboundedly with the sample size unless the data comes from a Gaussian distribution.

In[4]:=

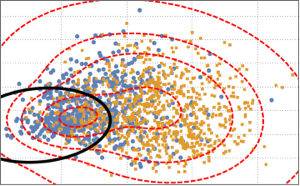
covm = {{2, 1, 0}, {1, 3, -1}, {0, -1, 2}}; ng\[ScriptCapitalD] = MultivariateTDistribution[covm, 12]; g\[ScriptCapitalD] = MultinormalDistribution[{0, 0, 0}, covm];

Draw samples from a multivariate t distribution and a multivariate normal distribution.

In[5]:=

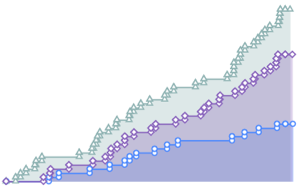
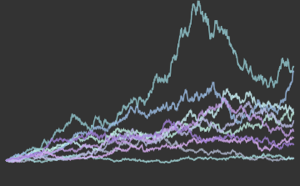
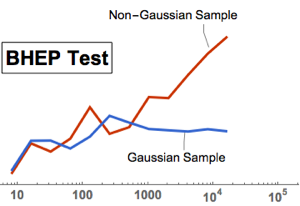
nongaussianData = RandomVariate[ng\[ScriptCapitalD], 2^14]; gaussianData = RandomVariate[g\[ScriptCapitalD], 2^14];

Compute and visualize the BHEP test statistics as a function of sample size.

In[6]:=

sizes = 2^Range[3, 14]; {nonGaussianTestStatistic, GaussianTestStatistic} = ParallelTable[{size, BaringhausHenzeTest[Take[d, size], "TestStatistic"]}, {d, {nongaussianData, gaussianData}}, {size, sizes}];

In[7]:=

ListLogLogPlot[{nonGaussianTestStatistic, GaussianTestStatistic}, PlotLegends -> {"Non-Gaussian", "Gaussian"}, ImageSize -> Medium, PlotRange -> All, FrameLabel -> {n, Subscript[T, n]}, PlotTheme -> "Detailed", Joined -> True]

Out[7]=