Inhomogeneous Poisson Process
An inhomogeneous Poisson process is a Poisson process with a time-varying rate. It can be used to model the arrival times of customers at a store, events of traffic, and positions of damage along a road. The probability density function of the process at any time slice t is Poisson distributed.
In[1]:=
PDF[InhomogeneousPoissonProcess[f[\[Tau]], \[Tau]][t], x]Out[1]=

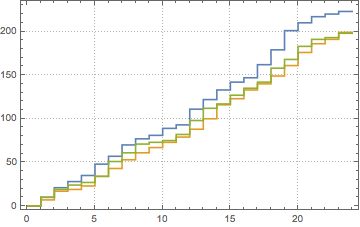
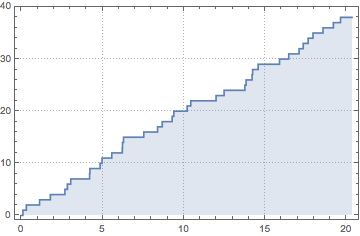
Simulate an inhomogeneous Poisson process.
In[2]:=
td = RandomFunction[
InhomogeneousPoissonProcess[2 + 1/(1 + t^2), t], {0, 20}];show complete Wolfram Language input
Out[3]=
An inhomogeneous Poisson process can be used to model arrival counts. Here, the process is used to simulate the number of arrivals at a small fast-food restaurant if the hourly arrival rates of customers are given.
In[4]:=

arrivalrates = {{0, 8}, {1, 9}, {2, 7}, {4, 6}, {5, 12}, {6, 14}, {7,
11}, {8, 6}, {9, 4}, {10, 3}, {11, 8}, {12, 15}, {13, 12}, {14,
10}, {15, 8}, {16, 6}, {17, 12}, {18, 17}, {19, 15}, {20,
12}, {21, 6}, {22, 5}, {23, 7}};
\[Lambda][t_] =
Interpolation[arrivalrates, InterpolationOrder -> 1][t];show complete Wolfram Language input
Out[5]=

Define an inhomogeneous Poisson process for the arrivals based on the given rate function λ(t) and simulate the arrival counts within a day.
In[6]:=
\[ScriptCapitalP] = InhomogeneousPoissonProcess[\[Lambda][t], t];
td = RandomFunction[\[ScriptCapitalP], {0, 23, 1}, 3];show complete Wolfram Language input
Out[7]=