Compare Weather in Chicago and European Capitals
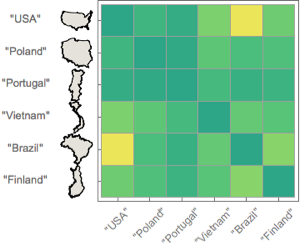
Find the capital city in the EU that had the most similar temperature to Chicago over the last year. Use WarpingDistance to determine the similarity between temperature sequences.
In[1]:=
chicagoTemp =
WeatherData["Chicago",
"Temperature", {{2015, 7}, {2016, 6}, "Week"}, "Value"];Get the temperature for all capital cities in the European Union.
In[2]:=
capitals = CityData /@ CountryData["EU", "CapitalCity"] // SortOut[2]=

In[3]:=

capitalsTemp =
WeatherData[#, "Temperature", {{2015, 7}, {2016, 6}, "Week"},
"Value"] -> # & /@ capitals;Find the capital city that has the most similar temperatures to Chicago.
In[4]:=
Nearest[capitalsTemp, chicagoTemp,
DistanceFunction -> (QuantityMagnitude@WarpingDistance[##] &)]Out[4]=
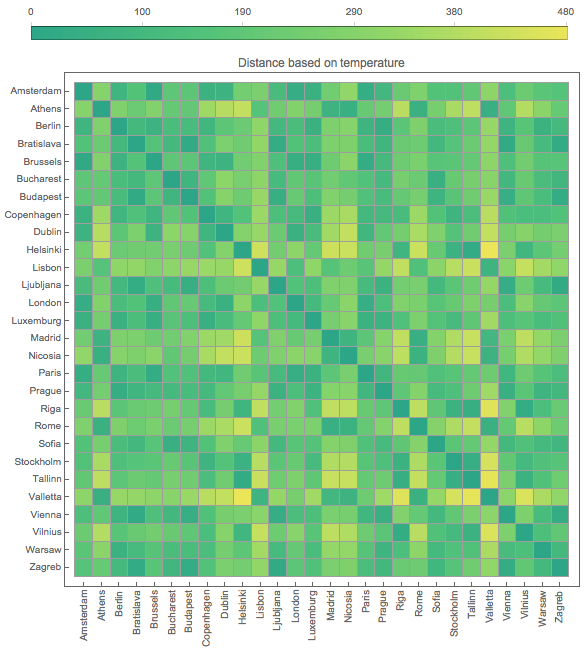
Calculate pairwise distances in a matrix.
In[5]:=
dm = DistanceMatrix[Keys@capitalsTemp,
DistanceFunction -> (QuantityMagnitude@WarpingDistance[##] &)];Show a 7×7 submatrix of the distance matrix.
In[6]:=
MatrixForm[Take[dm, 7, 7]]Out[6]//MatrixForm=

Visualize the temperature similarity using a previously computed distance matrix.
show complete Wolfram Language input
Out[7]=