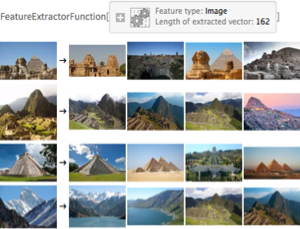
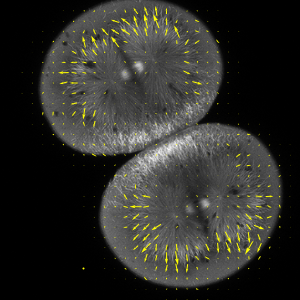
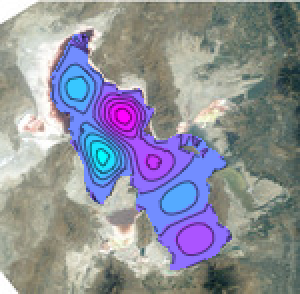
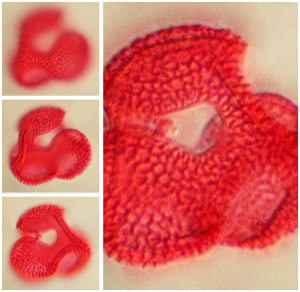
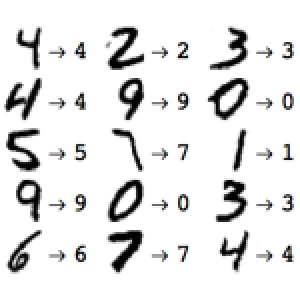多視点の再構築
三次元オブジェクトは,複数の二次元視点から再構築することが可能である.ImageDisplacementsを使って,1つの視点から次の視点への視差を見極める.視差の変動が大きいほど,対応する画素の後ろのオブジェクトにより近くなる.この深度の情報をもとに,ImageMeshとTriangulateMeshから得られるオブジェクトメッシュの頂点を押し出すことができる.結果は,三次元メッシュオブジェクト上にテクスチャをマップすることによって表示される.
In[1]:=

中央画像のオブジェクトマスクを得る.
In[2]:=
mask = Erosion[Binarize[imgs[[2]], 0], 1];中央画像に対する左と右の画像の視差を求める.
In[3]:=
parallaxL = First@ImageDisplacements[imgs[[{2, 1}]]];In[4]:=
parallaxR = First@ImageDisplacements[imgs[[{2, 3}]]];視差の合計にこれらの変位を組み合せる.
In[5]:=
parallax = parallaxL - parallaxR;指定の設定において,視差の ![]() 成分は対応する画素源の深度にだいたい比例している.
成分は対応する画素源の深度にだいたい比例している.
In[6]:=
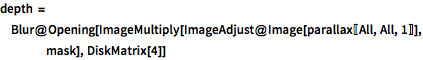
depth = Blur@
Opening[ImageMultiply[ImageAdjust@Image[parallax[[All, All, 1]]],
mask], DiskMatrix[4]]Out[6]=

深度の関数を構築する.
In[7]:=
depthFunction = ListInterpolation[Transpose@Reverse@ImageData[depth]];オブジェクトの突出によって細分化されたオブジェクトメッシュを得る.
In[8]:=
resolution = ImageAdjust@ImageSaliencyFilter[imgs[[2]]];In[9]:=
resolutionFunction =
ListInterpolation[Transpose@Reverse@ImageData@resolution];In[10]:=

\[CapitalOmega] = TriangulateMesh[
ImageMesh[Erosion[mask, DiskMatrix[2]]],
MeshRefinementFunction ->
Function[{vertices, area},
area > 32 + 512 (1 - resolutionFunction @@ Mean[vertices])^6]
]Out[10]=

オブジェクトメッシュを深度の関数で押し出す.
In[11]:=

Graphics3D[
GraphicsComplex[
Apply[{##, depthFunction[##]} &,
MeshCoordinates[\[CapitalOmega]], {1}],
{EdgeForm[], MeshCells[\[CapitalOmega], 2]}
],
PlotRange -> Append[Thread[{0, ImageDimensions[mask]}], {0, 1}],
BoxRatios -> {1, 1, 2/3},
ViewPoint -> Top
]Out[11]=

オブジェクトのテクスチャを中央画像から抽出する.
In[12]:=
texture = SetAlphaChannel[imgs[[2]], mask]Out[12]=

テクスチャを三次元オブジェクト上にマップする.
In[13]:=

Graphics3D[
{Texture[texture],
GraphicsComplex[
Apply[{##, depthFunction[##]} &,
MeshCoordinates[\[CapitalOmega]], {1}],
{EdgeForm[], MeshCells[\[CapitalOmega], 2]},
VertexTextureCoordinates ->
Map[#/ImageDimensions[texture] &, MeshCoordinates[\[CapitalOmega]]]
]
},
PlotRange -> Append[Thread[{0, ImageDimensions[mask]}], {0, 1}],
BoxRatios -> {1, 1, 2/3},
Lighting -> {{"Ambient", White}},
ViewPoint -> Top,
Boxed -> False
]