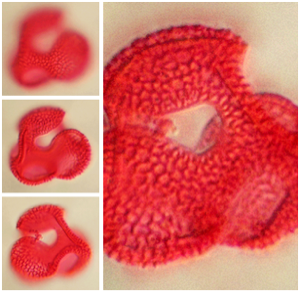
Многооконная Реконструкция: Новое в системе Wolfram Language 11

Многооконная Реконструкция

3D-объект может быть восстановлен на основе нескольких 2D изображений. Функция ImageDisplacements используется для определения параллакса от одного изображения к другому. Чем больше сдвиг параллакса, тем ближе объект позади соответствующего пикселя. С помощью этой информации, вы можете определить вершины объекта сетки, полученного с помощью функций ImageMesh и TriangulateMesh. Результат отображается путем наложения текстуры на 3D сетку.

In[1]:=

Получим объект-маску центрального изображения.

In[2]:=

mask = Erosion[Binarize[imgs[[2]], 0], 1];

Определим параллакс в левом и правом изображениях относительно центрального изображения.

In[3]:=

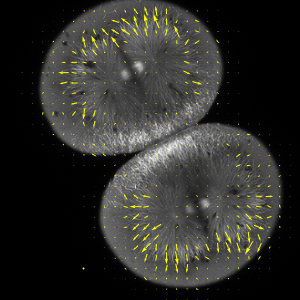
parallaxL = First@ImageDisplacements[imgs[[{2, 1}]]];

In[4]:=

parallaxR = First@ImageDisplacements[imgs[[{2, 3}]]];

Сочетаем перемещения, выполненные в предыдущем шаге, в общем параллаксе.

In[5]:=

parallax = parallaxL - parallaxR;

В данном случае, Х-компонент параллакса примерно пропорционален глубине соответствующего источника пикселей.

In[6]:=

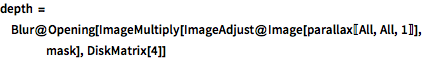
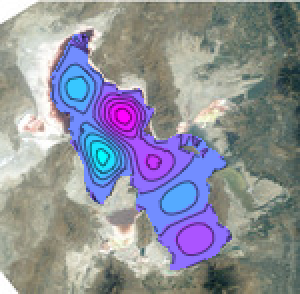
depth = Blur@
  Opening[ImageMultiply[ImageAdjust@Image[parallax[[All, All, 1]]], 
    mask], DiskMatrix[4]]

Out[6]=

Построим функцию глубины.

In[7]:=

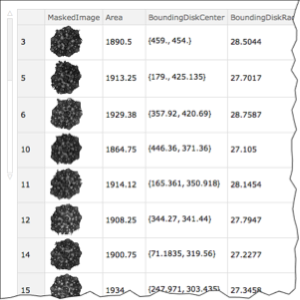
depthFunction = ListInterpolation[Transpose@Reverse@ImageData[depth]];

Получим более точный объект-сетку, с уточнением, зависящим от значимости этого объекта.

In[8]:=

resolution = ImageAdjust@ImageSaliencyFilter[imgs[[2]]];

In[9]:=

resolutionFunction = 
  ListInterpolation[Transpose@Reverse@ImageData@resolution];

In[10]:=

\[CapitalOmega] = TriangulateMesh[
  ImageMesh[Erosion[mask, DiskMatrix[2]]], 
  MeshRefinementFunction -> 
   Function[{vertices, area}, 
    area > 32 + 512 (1 - resolutionFunction @@ Mean[vertices])^6]
  ]

Out[10]=

Осуществим выдавливание объекта-сетки с помощью функции глубины.

In[11]:=

Graphics3D[
 GraphicsComplex[
  Apply[{##, depthFunction[##]} &, 
   MeshCoordinates[\[CapitalOmega]], {1}],
  {EdgeForm[], MeshCells[\[CapitalOmega], 2]}
  ],
 PlotRange -> Append[Thread[{0, ImageDimensions[mask]}], {0, 1}],
 BoxRatios -> {1, 1, 2/3},
 ViewPoint -> Top
 ]

Out[11]=

Определим текстуру объекта на основе центрального изображения.

In[12]:=

texture = SetAlphaChannel[imgs[[2]], mask]

Out[12]=

Наложим полученную текстуру на 3D объект.

In[13]:=

Graphics3D[
 {Texture[texture],
  GraphicsComplex[
   Apply[{##, depthFunction[##]} &, 
    MeshCoordinates[\[CapitalOmega]], {1}],
   {EdgeForm[], MeshCells[\[CapitalOmega], 2]},
   VertexTextureCoordinates -> 
    Map[#/ImageDimensions[texture] &, MeshCoordinates[\[CapitalOmega]]]
   ]
  },
 PlotRange -> Append[Thread[{0, ImageDimensions[mask]}], {0, 1}],
 BoxRatios -> {1, 1, 2/3},
 Lighting -> {{"Ambient", White}},
 ViewPoint -> Top,
 Boxed -> False
 ]