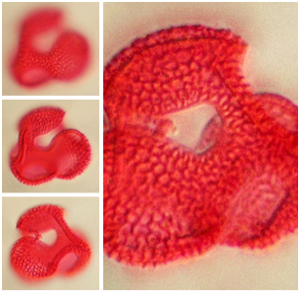
利用多个视图重建三维物体
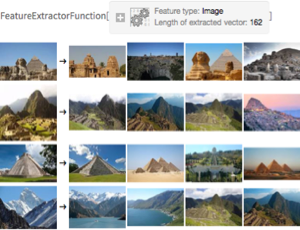
由多个二维视图可以重建一个三维物体. ImageDisplacements 被用来确定一个视图到下一个视图间的视差. 视差越大,相应像素对应的物体越近. 利用这种深度信息,可以拉伸通过 ImageMesh 和 TriangulateMesh 获得的物体的网格对象的顶点. 然后通过在三维网格物体上进行纹理映射显示结果.
In[1]:=

获取中间图像的对象掩膜 (object mask).
In[2]:=
mask = Erosion[Binarize[imgs[[2]], 0], 1];确定左边图像和右边图像相对于中间图像的视差.
In[3]:=
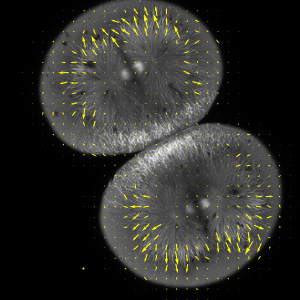
parallaxL = First@ImageDisplacements[imgs[[{2, 1}]]];In[4]:=
parallaxR = First@ImageDisplacements[imgs[[{2, 3}]]];将这些位移组合成总视差.
In[5]:=
parallax = parallaxL - parallaxR;在这种情况下,视差的 ![]() 分量大约与各自的像素源的深度成正比.
分量大约与各自的像素源的深度成正比.
In[6]:=
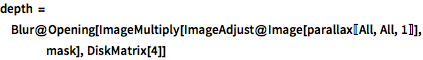
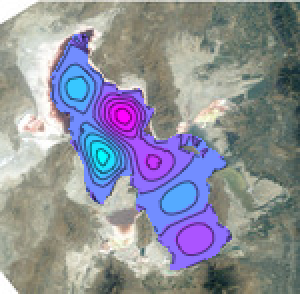
depth = Blur@
Opening[ImageMultiply[ImageAdjust@Image[parallax[[All, All, 1]]],
mask], DiskMatrix[4]]Out[6]=

构建深度函数.
In[7]:=
depthFunction = ListInterpolation[Transpose@Reverse@ImageData[depth]];根据物体的显著性进行细化,从而获取物体的网格对象.
In[8]:=
resolution = ImageAdjust@ImageSaliencyFilter[imgs[[2]]];In[9]:=
resolutionFunction =
ListInterpolation[Transpose@Reverse@ImageData@resolution];In[10]:=

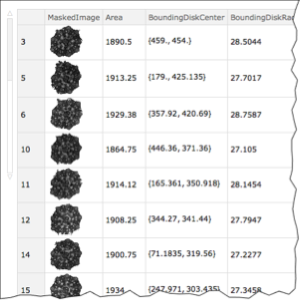
\[CapitalOmega] = TriangulateMesh[
ImageMesh[Erosion[mask, DiskMatrix[2]]],
MeshRefinementFunction ->
Function[{vertices, area},
area > 32 + 512 (1 - resolutionFunction @@ Mean[vertices])^6]
]Out[10]=
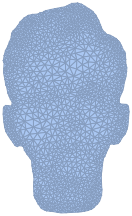
用深度函数拉伸物体的网格对象.
In[11]:=

Graphics3D[
GraphicsComplex[
Apply[{##, depthFunction[##]} &,
MeshCoordinates[\[CapitalOmega]], {1}],
{EdgeForm[], MeshCells[\[CapitalOmega], 2]}
],
PlotRange -> Append[Thread[{0, ImageDimensions[mask]}], {0, 1}],
BoxRatios -> {1, 1, 2/3},
ViewPoint -> Top
]Out[11]=

从中间的图像上提取物体的纹理.
In[12]:=
texture = SetAlphaChannel[imgs[[2]], mask]Out[12]=

将纹理映射到三维物体上.
In[13]:=

Graphics3D[
{Texture[texture],
GraphicsComplex[
Apply[{##, depthFunction[##]} &,
MeshCoordinates[\[CapitalOmega]], {1}],
{EdgeForm[], MeshCells[\[CapitalOmega], 2]},
VertexTextureCoordinates ->
Map[#/ImageDimensions[texture] &, MeshCoordinates[\[CapitalOmega]]]
]
},
PlotRange -> Append[Thread[{0, ImageDimensions[mask]}], {0, 1}],
BoxRatios -> {1, 1, 2/3},
Lighting -> {{"Ambient", White}},
ViewPoint -> Top,
Boxed -> False
]