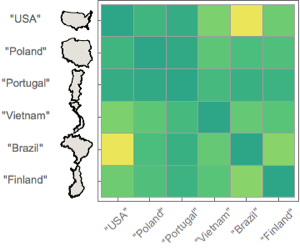
グレートソルト湖の波
ImageMeshを使うと,画像セグメントをBoundaryMeshRegionオブジェクトに変換することができる.これらのメッシュ領域は,有限要素法(FEM)等の他の分野での関数の利用を可能にする.
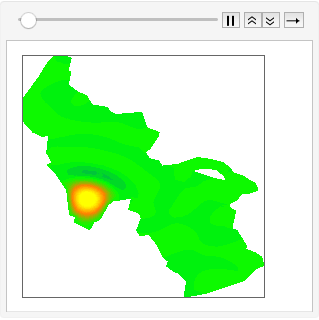
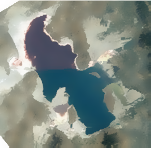
このFEMとの関連を示すために,ユタ州のグレートソルト湖の表面の波の主要なモードを求める.
In[1]:=
img = EntityValue[Entity["Lake", "GreatSaltLake::yw8cf"], "Image"]Out[1]=

画像を平均シフトフィルタで正規化する.
In[2]:=
img2 = MeanShiftFilter[img, 3, 0.1]Out[2]=
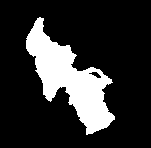
領域拡張法を使ってセグメンテーションを得る.
In[3]:=
mask = RegionBinarize[img2, \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJzt1jEKwkAQQNFdK0uv4C1sLW0VD6AYxSZCFMRzCJ7XiF3SzFb7lf8ggUCK
D8MmM99f1sdJSuk67W/r3X3ZdbvHZtY/bNvr+dQ2h1V7a05Nt9h/Xnv21ytJ
kiRJkiRJkn5H7tVuGLMqzqo4q+KsiuNW8bKsimNWfbNwXVbF5Yzuqp0xZFUB
dBaui5kF/T5AsxJ1jNAsq0qgs3BlOSPDMrMLmvUBDcNnsbqov2x4FrWrdscA
NIu6SjCzoEOEZlGniF5Ta0eMmVXCqjjmCJlV5KzaDWNWxXGreFnMKvAIazeM
MUfIXEmtKsCs8hSWsCrOqjhmlSRJkiRJkvS/3tRrD1M=
"], {{0, 147}, {150,
0}}, {0, 1},
ColorFunction->GrayLevel],
BoxForm`ImageTag["Bit", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{150, 147},
PlotRange->{{0, 150}, {0, 147}}]\), 1/5]Out[3]=
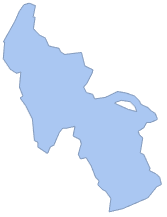
湖の表面のBoundaryMeshRegionオブジェクトを取り出す.
In[4]:=
\[ScriptCapitalR] = ImageMesh[mask]Out[4]=
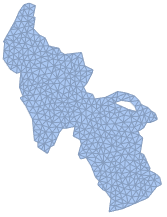
湖の表面のメッシュを作成する.
In[5]:=
\[CapitalOmega] =
TriangulateMesh[\[ScriptCapitalR], MaxCellMeasure -> 8]Out[5]=
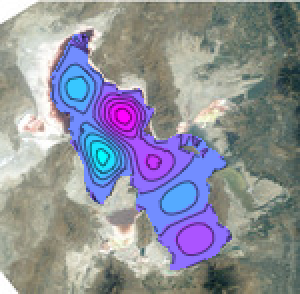
湖の領域内のラプラシアンの固有関数を求めることによって,湖の表面の波動方程式を解く.
In[6]:=
\[ScriptCapitalL] = -\!\(
\*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(\[CurlyPhi][x,
y]\)\);境界条件を使う.
In[7]:=
\[ScriptCapitalB] = DirichletCondition[\[CurlyPhi][x, y] == 0, True];固有関数Φの正規直交基底を固有値Λで生成する.
In[8]:=
{\[CapitalLambda], \[CapitalPhi]} =
NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, \[CurlyPhi][x,
y], {x, y} \[Element] \[CapitalOmega], 64];最初の6個の振動モードを表示する.
In[9]:=

GraphicsGrid[
Partition[
Table[ContourPlot[\[CapitalPhi][[
k]], {x, y} \[Element] \[CapitalOmega], PlotRange -> All,
PlotLabel -> \[CapitalLambda][[k]], PlotTheme -> "Minimal"], {k,
6}],
3
],
ImageSize -> 512
]Out[9]=
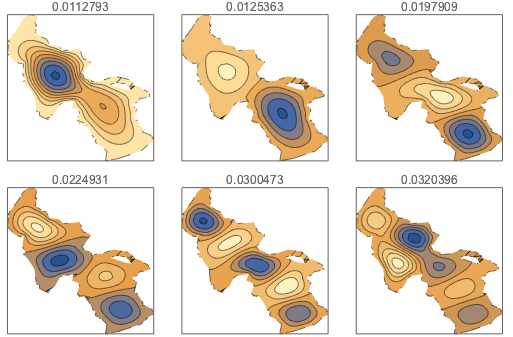
減衰振動モードの時間的進化は以下で与えられる.
In[10]:=
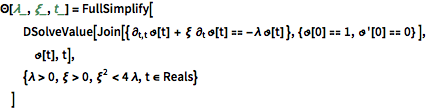
\[CapitalTheta][\[Lambda]_, \[Xi]_, t_] = FullSimplify[
DSolveValue[Join[{ \!\(
\*SubscriptBox[\(\[PartialD]\), \(t,
t\)]\(\(TraditionalForm\`\[CurlyTheta]\)[
t]\)\) + \[Xi] \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(\(TraditionalForm\`\
\[CurlyTheta]\)[
t]\)\) == -\[Lambda] \!\(TraditionalForm\`\[CurlyTheta]\)[
t] }, {\!\(TraditionalForm\`\[CurlyTheta]\)[0] ==
1, \[CurlyTheta]'[0] ==
0} ], \!\(TraditionalForm\`\[CurlyTheta]\)[t], t],
{\[Lambda] > 0, \[Xi] > 0, \[Xi]^2 < 4 \[Lambda], t \[Element] Reals}
]Out[10]=
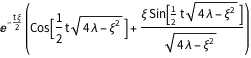
固有関数の初期摂動を拡張し,それらを時間で進化させると,湖面上の波の伝播のシミュレーションが得られる.
完全なWolfram言語入力を表示する