Язык Wolfram Language™

Волны в Большом Соленом озере

Using ImageMesh, позволяет преобразовать сегменты изображения в граничные сетчатые области . Cетчатые области позволяют использовать функции сразу для нескольких областей, например, методом конечных элементов (МКЭ).

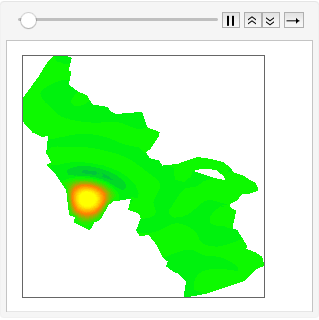
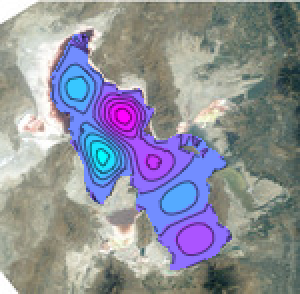
В качестве иллюстрации применения метода конечных элементов, определим основные виды поверхностных волн в Большом Соленом озере в штате Юта.

In[1]:=

img = EntityValue[Entity["Lake", "GreatSaltLake::yw8cf"], "Image"]

Out[1]=

Упорядочим изображение с помощью среднесменного фильтра.

In[2]:=

img2 = MeanShiftFilter[img, 3, 0.1]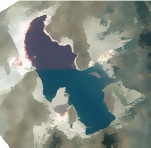

Out[2]=

Выделим сегмент формы озера.

In[3]:=

mask = RegionBinarize[img2, \!\(\* GraphicsBox[ TagBox[RasterBox[CompressedData[" 1:eJzt1jEKwkAQQNFdK0uv4C1sLW0VD6AYxSZCFMRzCJ7XiF3SzFb7lf8ggUCK D8MmM99f1sdJSuk67W/r3X3ZdbvHZtY/bNvr+dQ2h1V7a05Nt9h/Xnv21ytJ kiRJkiRJkn5H7tVuGLMqzqo4q+KsiuNW8bKsimNWfbNwXVbF5Yzuqp0xZFUB dBaui5kF/T5AsxJ1jNAsq0qgs3BlOSPDMrMLmvUBDcNnsbqov2x4FrWrdscA NIu6SjCzoEOEZlGniF5Ta0eMmVXCqjjmCJlV5KzaDWNWxXGreFnMKvAIazeM MUfIXEmtKsCs8hSWsCrOqjhmlSRJkiRJkvS/3tRrD1M= "], {{0, 147}, {150, 0}}, {0, 1}, ColorFunction->GrayLevel], BoxForm`ImageTag["Bit", ColorSpace -> Automatic, Interleaving -> None], Selectable->False], DefaultBaseStyle->"ImageGraphics", ImageSizeRaw->{150, 147}, PlotRange->{{0, 150}, {0, 147}}]\), 1/5]

Out[3]=

Извлечем объект поверхности озера типа граничной сетчатой области.

In[4]:=

\[ScriptCapitalR] = ImageMesh[mask]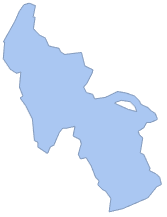

Out[4]=

Создадим сетку поверхности озера.

In[5]:=

\[CapitalOmega] = TriangulateMesh[\[ScriptCapitalR], MaxCellMeasure -> 8]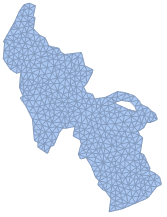

Out[5]=

Для решения волнового уравнения поверхности озера, сначала определим собственные функции лапласиана внутри региона озера.

In[6]:=

\[ScriptCapitalL] = -\!\( \*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(\[CurlyPhi][x, y]\)\);

Будем использовать граничное условие.

In[7]:=

\[ScriptCapitalB] = DirichletCondition[\[CurlyPhi][x, y] == 0, True];

Создадим ортонормированную базу из собственных функций Φ с собственными значениями Λ.

In[8]:=

{\[CapitalLambda], \[CapitalPhi]} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, \[CurlyPhi][x, y], {x, y} \[Element] \[CapitalOmega], 64];

Отобразим первые шесть режимов колебаний волн.

In[9]:=

GraphicsGrid[ Partition[ Table[ContourPlot[\[CapitalPhi][[ k]], {x, y} \[Element] \[CapitalOmega], PlotRange -> All, PlotLabel -> \[CapitalLambda][[k]], PlotTheme -> "Minimal"], {k, 6}], 3 ], ImageSize -> 512 ]

Out[9]=

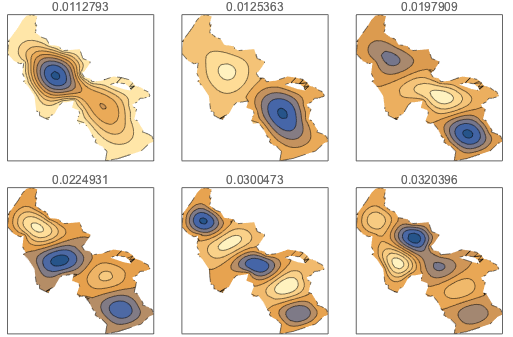
Временные изменения в модах колебаний задаются следующим образом.

In[10]:=

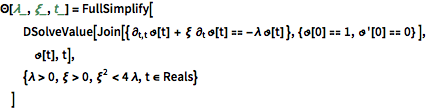
\[CapitalTheta][\[Lambda]_, \[Xi]_, t_] = FullSimplify[ DSolveValue[Join[{ \!\( \*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(\(TraditionalForm\`\[CurlyTheta]\)[ t]\)\) + \[Xi] \!\( \*SubscriptBox[\(\[PartialD]\), \(t\)]\(\(TraditionalForm\`\ \[CurlyTheta]\)[ t]\)\) == -\[Lambda] \!\(TraditionalForm\`\[CurlyTheta]\)[ t] }, {\!\(TraditionalForm\`\[CurlyTheta]\)[0] == 1, \[CurlyTheta]'[0] == 0} ], \!\(TraditionalForm\`\[CurlyTheta]\)[t], t], {\[Lambda] > 0, \[Xi] > 0, \[Xi]^2 < 4 \[Lambda], t \[Element] Reals} ]

Out[10]=

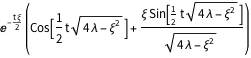
Анализ начального колебания и их дальнейшей динамики с помощью собственных функций позволяет моделировать движение волн на поверхности озера.

In[11]:=

n = 64; weights = Take[GaussianMatrix[{{n}, n/2}], -n - 1]; weights -= Last[weights]; weights = Most[weights]; weights *= 1/First[weights]; wave[t_] = (\[CapitalTheta][\[CapitalLambda], 0.005, t] weights (\[CapitalPhi] /. {x -> 50, y -> 60} )) . \[CapitalPhi]; waveColors = (Blend[{{-0.01, Purple}, {-0.005, Blue}, {0., Green}, {0.005, Orange}, {0.01, Yellow}}, #] &); anim = Table[ ContourPlot[ wave[t], {x, y} \[Element] \[CapitalOmega], PlotRange -> {-0.01, 0.012}, Contours -> Range[-0.01, 0.012, 0.0005], PlotTheme -> "Minimal", ColorFunctionScaling -> False, ContourStyle -> None, ColorFunction -> waveColors ], {t, 0, 255, 1} ]; ListAnimate[anim]

Запустить анимацию

Остановить анимацию