Wolfram Language™

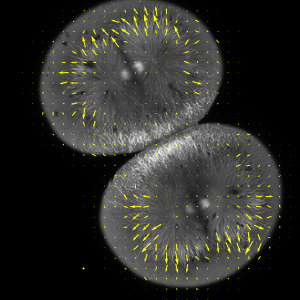
Ondas en el Gran Lago Salado

Usando ImageMesh, usted puede convertir segmentos de imagen en objetos de BoundaryMeshRegion. Estas regiones de malla le permiten utilizar funciones en otras áreas, tales como métodos de elementos finitos (FEM).

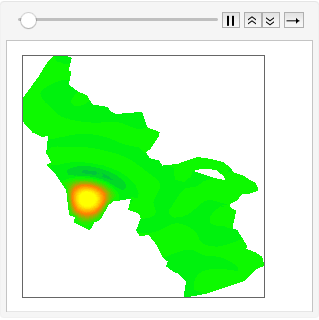
Para ilustrar esta conexión FEM, determine los modos principales modos de ondas superficiales en el Gran Lago Salado en Utah.

In[1]:=

img = EntityValue[Entity["Lake", "GreatSaltLake::yw8cf"], "Image"]

Out[1]=

Regularice la imagen con el filtro de media de desplazamiento.

In[2]:=

img2 = MeanShiftFilter[img, 3, 0.1]

Out[2]=

Obtenga una segmentación por medio de una región en crecimiento.

In[3]:=

mask = RegionBinarize[img2, \!\(\* GraphicsBox[ TagBox[RasterBox[CompressedData[" 1:eJzt1jEKwkAQQNFdK0uv4C1sLW0VD6AYxSZCFMRzCJ7XiF3SzFb7lf8ggUCK D8MmM99f1sdJSuk67W/r3X3ZdbvHZtY/bNvr+dQ2h1V7a05Nt9h/Xnv21ytJ kiRJkiRJkn5H7tVuGLMqzqo4q+KsiuNW8bKsimNWfbNwXVbF5Yzuqp0xZFUB dBaui5kF/T5AsxJ1jNAsq0qgs3BlOSPDMrMLmvUBDcNnsbqov2x4FrWrdscA NIu6SjCzoEOEZlGniF5Ta0eMmVXCqjjmCJlV5KzaDWNWxXGreFnMKvAIazeM MUfIXEmtKsCs8hSWsCrOqjhmlSRJkiRJkvS/3tRrD1M= "], {{0, 147}, {150, 0}}, {0, 1}, ColorFunction->GrayLevel], BoxForm`ImageTag["Bit", ColorSpace -> Automatic, Interleaving -> None], Selectable->False], DefaultBaseStyle->"ImageGraphics", ImageSizeRaw->{150, 147}, PlotRange->{{0, 150}, {0, 147}}]\), 1/5]

Out[3]=

Recupere un objeto de BoundaryMeshRegion de la superficie del lago.

In[4]:=

\[ScriptCapitalR] = ImageMesh[mask]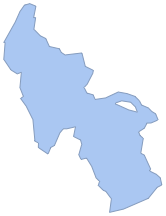

Out[4]=

Cree una malla de la superficie del lago.

In[5]:=

\[CapitalOmega] = TriangulateMesh[\[ScriptCapitalR], MaxCellMeasure -> 8]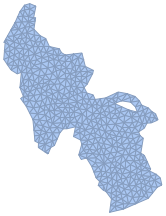

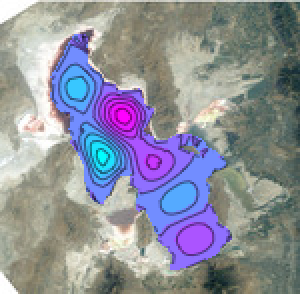
Out[5]=

Resuelva la ecuación de onda de la superficie del lago determinando las funciones propias de laplaciano dentro de la región del lago.

In[6]:=

\[ScriptCapitalL] = -\!\( \*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(\[CurlyPhi][x, y]\)\);

Usando una condición de límite.

In[7]:=

\[ScriptCapitalB] = DirichletCondition[\[CurlyPhi][x, y] == 0, True];

Genere una base ortonormal de funciones propias Φ con valores propios Λ.

In[8]:=

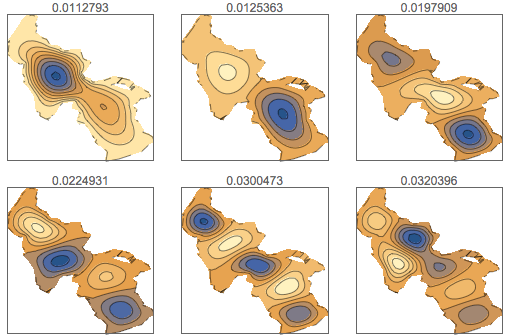
{\[CapitalLambda], \[CapitalPhi]} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, \[CurlyPhi][x, y], {x, y} \[Element] \[CapitalOmega], 64];

Muestre los primeros seis modos de oscilaciones.

In[9]:=

GraphicsGrid[ Partition[ Table[ContourPlot[\[CapitalPhi][[ k]], {x, y} \[Element] \[CapitalOmega], PlotRange -> All, PlotLabel -> \[CapitalLambda][[k]], PlotTheme -> "Minimal"], {k, 6}], 3 ], ImageSize -> 512 ]

Out[9]=

La evolución temporal de los modos de oscilación decadente es dada como sigue.

In[10]:=

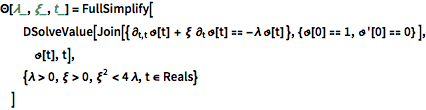
\[CapitalTheta][\[Lambda]_, \[Xi]_, t_] = FullSimplify[ DSolveValue[Join[{ \!\( \*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(\(TraditionalForm\`\[CurlyTheta]\)[ t]\)\) + \[Xi] \!\( \*SubscriptBox[\(\[PartialD]\), \(t\)]\(\(TraditionalForm\`\ \[CurlyTheta]\)[ t]\)\) == -\[Lambda] \!\(TraditionalForm\`\[CurlyTheta]\)[ t] }, {\!\(TraditionalForm\`\[CurlyTheta]\)[0] == 1, \[CurlyTheta]'[0] == 0} ], \!\(TraditionalForm\`\[CurlyTheta]\)[t], t], {\[Lambda] > 0, \[Xi] > 0, \[Xi]^2 < 4 \[Lambda], t \[Element] Reals} ]

Out[10]=

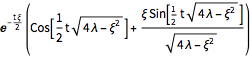
Por medio de la expansión de una perturbación inicial en funciones propias y dejando que estas evolucionen en el tiempo, se obtiene una propagación de ondas en el lago.

In[11]:=

n = 64; weights = Take[GaussianMatrix[{{n}, n/2}], -n - 1]; weights -= Last[weights]; weights = Most[weights]; weights *= 1/First[weights]; wave[t_] = (\[CapitalTheta][\[CapitalLambda], 0.005, t] weights (\[CapitalPhi] /. {x -> 50, y -> 60} )) . \[CapitalPhi]; waveColors = (Blend[{{-0.01, Purple}, {-0.005, Blue}, {0., Green}, {0.005, Orange}, {0.01, Yellow}}, #] &); anim = Table[ ContourPlot[ wave[t], {x, y} \[Element] \[CapitalOmega], PlotRange -> {-0.01, 0.012}, Contours -> Range[-0.01, 0.012, 0.0005], PlotTheme -> "Minimal", ColorFunctionScaling -> False, ContourStyle -> None, ColorFunction -> waveColors ], {t, 0, 255, 1} ]; ListAnimate[anim]

Reproducir

Detener