‹›Knowledgebase ExpansionTransform Anatomical Structures into Sculpture
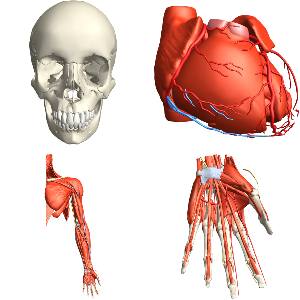
With the availability of high‐resolution 3D models of human anatomical structures, the powerful graphics and region‐processing functionality in Version 11 can be used to programmatically construct anatomy-based modern sculpture.
The art of Antony Gormley can serve as an inspiration (http://www.antonygormley.com/sculpture/chronology).
show complete Wolfram Language input
WikipediaData["Antony Gormley", "ImageList"] //
Select[#,
Length[Union[#]]/Length[#] &[ImageData[#][[1, 1]]] > 0.8 &] &Load a faithful representation of the human body.
human = AnatomyData[Entity["AnatomicalStructure", "Skin"],
"MeshRegion"]Using the regions functionality, it is straightforward to build a large variety of sculptures.
show complete Wolfram Language input
pts = MeshCoordinates[human];
nf = Nearest[pts];
color := Directive[GrayLevel[RandomReal[{0.5, 0.7}]],
Specularity[RandomColor[], RandomInteger[{10, 20}]]]With[{dode = N[PolyhedronData["Dodecahedron"][[1]]]},
ballToDodecahedron[Ball[p_, r_]] :=
Translate[
Scale[Rotate[dode, RandomReal[{-Pi, Pi}],
RandomReal[{-1, 1}, 3], {0, 0, 0}], r], p]]GraphicsGrid[
Partition[#,
4] &@{Graphics3D[{EdgeForm[], color,
Table[BoundingRegion[
nf[RandomChoice[pts], RandomInteger[{100, 1000}]],
"MinCuboid"], {200}]}],
Graphics3D[{EdgeForm[], color,
Table[BoundingRegion[
nf[RandomChoice[pts], RandomInteger[{100, 1000}]],
"FastOrientedCuboid"], {250}]}],
Graphics3D[{color, EdgeForm[],
Table[Show[
BoundingRegion[
RandomChoice[
nf[RandomChoice[pts], RandomInteger[{100, 2000}]],
RandomInteger[{4, 12}]], "MinConvexPolyhedron"]][[
1]] /. _Directive :> {}, {600}]}],
Graphics3D[{color, EdgeForm[],
Table[ballToDodecahedron@
BoundingRegion[
RandomChoice[nf[RandomChoice[pts], RandomInteger[{100, 600}]],
RandomInteger[{4, 12}]], "FastBall"], {300}]}],
Graphics3D[{color,
Table[BoundingRegion[
RandomChoice[
nf[RandomChoice[pts], RandomInteger[{100, 600}]],
RandomInteger[{4, 12}]], "FastBall"], {500}]}],
Graphics3D[{color,
Table[
BoundingRegion[
RandomChoice[nf[RandomChoice[pts], RandomInteger[{100, 2000}]],
RandomInteger[{4, 12}]], "FastEllipsoid"], {350}]}],
Graphics3D[{color, EdgeForm[],
Table[Cylinder[{#, nf[#, RandomInteger[{2000, 5000}]][[-1]]} &[
RandomChoice[pts]],
RandomReal[{5, 25}]], {600}]}],
Module[{pts2 = RandomSample[pts, 6000], nf2},
nf2 = Nearest[pts];
Graphics3D[{color, EdgeForm[], CapForm["Round"],
Cylinder[{#, nf2[#, 100][[-1]]}, 6] & /@
RandomSample[pts2]}]]}, Spacings -> {-150, Automatic},
ImageSize -> Full
] // Rasterize[#, "Image", ImageSize -> {400, 400}] &More classical-appearing art can be generated by applying a rotation and stretching transform to the legs and arms to make angel‐like sculptures.
show complete Wolfram Language input
nonlinearTransform3D[expr_, g_] :=
Module[{gD, inv, newNormal, newVertices, newNormals},
gD[x_, y_, z_] =
Compile[{x, y, z}, Evaluate[D[g[{x, y, z}], {{x, y, z}}]]];
inv[m_] :=
With[{im = Inverse[m]},
If[Head[im] === Inverse, m, PseudoInverse[m]]];
newNormal[{vertex_, normal_}] :=
Quiet[With[{m = inv[Transpose[gD[vertex]]]},
If[Sign[Det[m]] == -1, -1, 1] m.normal]];
expr /. {GraphicsComplex[vertices_, body_, a___,
VertexNormals -> normals_,
b___] :> (newVertices = g /@ vertices;
newNormals = newNormal /@ Transpose[{vertices, normals}];
GraphicsComplex[newVertices, body, a,
VertexNormals -> newNormals, b])}]doubleTwist[{x_, y_, z_}] :=
With[{h = 1000, w = 180, H = 1300, \[Xi] = 600, \[Kappa] = 150},
With[{\[CurlyPhi] =
6 Pi If[z > h || (z > \[Xi] && Sqrt[x^2] > w), 0,
Cos[Pi/2 (h - z)/h]],
\[CurlyTheta] = -1.6 Pi If[(z > \[Xi] && Sqrt[x^2] < w) ||
z < \[Xi], 0, Cos[Pi/2 (w - x)/w]],
f = Piecewise[{{1, z > h}, {1 + (h - z)/h, z < h}}],
g = If[(z > \[Xi] && Sqrt[x^2] < w) || z < \[Xi], 1,
1 + (Sqrt[x^2] - w)/\[Kappa]]}, {{g, 0, 0}, {0,
Cos[\[CurlyTheta]],
Sin[\[CurlyTheta]]}, {0, -Sin[\[CurlyTheta]],
Cos[\[CurlyTheta]]}}.({{f Cos[\[CurlyPhi]], f Sin[\[CurlyPhi]],
0}, {-f Sin[\[CurlyPhi]], f Cos[\[CurlyPhi]], 0}, {0, 0,
1}}.{x, y, z} - {0, 0, H}) + {0, 0, H}]]smoothHuman = Entity["AnatomicalStructure", "Skin"]["Graphics3D"];Show[nonlinearTransform3D[smoothHuman, doubleTwist],
ViewPoint -> {-1, -2, 0}, Method -> {"ShrinkWrap" -> True}]