Model the Composition of the Universe over Time

Explore how the composition of the universe changes over time, according to the standard ΛCDM (Lambda cold dark matter) model.

Compute the values of the density ratios of dark energy, matter, and radiation at different ages of the universe, ranging from 1000 years to 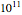years.

In[1]:=

ages = Quantity[10^Range[3, 11, 0.2], "Years"];

In[2]:=

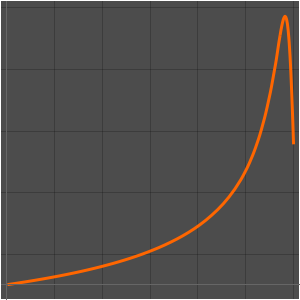
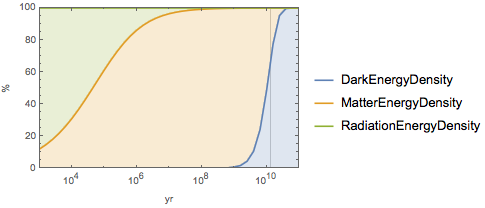
darkenergy = Table[UniverseModelData[t, "DarkEnergyDensityRatio"], {t, ages}]; matter = Table[ UniverseModelData[t, "MatterEnergyDensityRatio"], {t, ages}]; radiation = Table[UniverseModelData[t, "RadiationEnergyDensityRatio"], {t, ages}];

Represent the evolution in time for the three components, denoting the current age of the universe with a vertical bar. Currently the largest component is dark energy.

In[3]:=

data = { Transpose[{ages, darkenergy}], Transpose[{ages, darkenergy + matter}], Transpose[{ages, darkenergy + matter + radiation}] }; ListLogLinearPlot[data, PlotRange -> All, Joined -> True, Filling -> {1 -> Axis, 2 -> {1}, 3 -> {2}}, FrameLabel -> Automatic, GridLines -> {{13.8*10^9}, None}, PlotRangePadding -> 0, Frame -> True, PlotLegends -> {"DarkEnergyDensity", "MatterEnergyDensity", "RadiationEnergyDensity"}]

Out[3]=

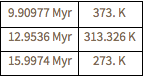
Discover when the background radiation temperature would have been between 273 and 373 K (the "Habitable Epoch" of the universe).

In[4]:=

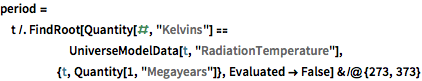
period = t /. FindRoot[ Quantity[#, "Kelvins"] == UniverseModelData[t, "RadiationTemperature"], {t, Quantity[1, "Megayears"]}, Evaluated -> False] & /@ {273, 373}

Out[4]=

In[5]:=

Grid[{#, UniverseModelData[#, "RadiationTemperature"]} & /@ Through[{Min, Mean, Max}[period]], Dividers -> All]

Out[5]=