多様体のパラメータ化を学ぶ
もとの入力の再構築を学習する「ボトルネック」層付きネットワーク,オートエンコーダを使うことによって,入力データが存在する多様体のパラメータ化を学ぶ.
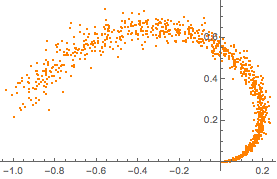
合成の二次元多様体の一部から訓練データのサンプルを抽出する.
In[1]:=

manifold =
Table[AngleVector[{x, 0.9 Pi x}] +
x/20*RandomVariate[NormalDistribution[], 2], {x, 0, 1, 0.001}];
plot = ListPlot[manifold, PlotStyle -> Orange]Out[1]=
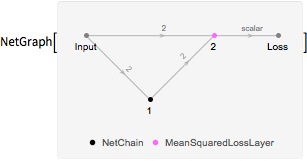
多様体のパラメータ化を学ぶために,「ボトルネック」層を含むネットワークを生成する.
In[2]:=
net = NetChain[{25, Ramp, 1, 25, Ramp, 2}, "Input" -> 2]Out[2]=

ネットワークが入力と同一の出力を生成することのできる度合いを測定する「再構築エラー」に基づいて損失を計算する損失ネットワークを作成する.
In[3]:=
lossNet =
NetGraph[{net, MeanSquaredLossLayer[]}, {1 -> 2,
NetPort["Input"] -> NetPort[2, "Target"]}]Out[3]=
多様体の損失ネットワークを訓練し,損失ネットワークからもとのネットワークを抽出する.
In[4]:=
lossNet =
NetTrain[lossNet, <|"Input" -> manifold|>, BatchSize -> 4096];
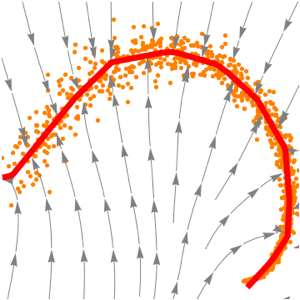
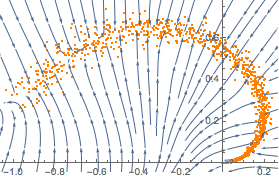
trained = NetExtract[lossNet, 1];ネットワークが任意の点を多様体上にどのように投影するかを可視化する.
In[5]:=
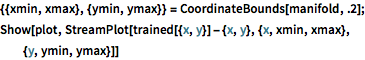
{{xmin, xmax}, {ymin, ymax}} = CoordinateBounds[manifold, .2];
Show[plot,
StreamPlot[
trained[{x, y}] - {x, y}, {x, xmin, xmax}, {y, ymin, ymax}]]Out[5]=
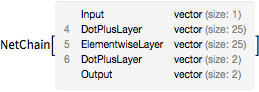
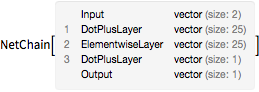
ネットワークを「エンコーダ」と「デコーダ」に分割する.エンコーダは単独のスカラー値を使って点をパラメータ化し,デコーダはこのパラメータ化から点を再構築する.
In[6]:=
decoder = Drop[trained, 3]
encoder = Take[trained, 3]Out[6]=
Out[6]=
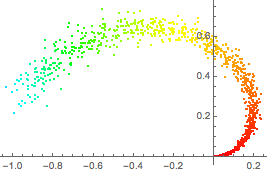
エンコーダによるパラメータ化によってもとの多様体の各点を色付けする.
In[7]:=
ListPlot[Style[#, Hue[First[0.3 + encoder[#]]/3]] & /@ manifold]Out[7]=
エンコーダを多様体に適用することにより,パラメータ化の範囲を得る.
In[8]:=
{min, max} = MinMax[encoder[manifold]]Out[8]=
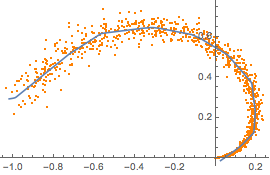
もとの多様体とともにこの範囲上の再構築を表示する.
In[9]:=
Show[plot, ListLinePlot[Table[decoder[x], {x, min, max, .01}]]]Out[9]=