学习一个流形的参数化
使用自动编码器,学习输入数据所处流形的参数化. 自动编码器是一个具有“瓶颈”层的、通过学习来重构原始输入的网络.
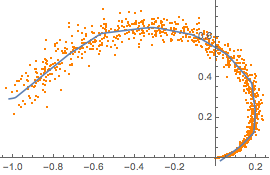
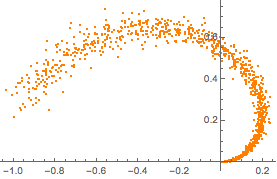
从合成的二维流形的一部分中进行训练数据取样.
In[1]:=

manifold =
Table[AngleVector[{x, 0.9 Pi x}] +
x/20*RandomVariate[NormalDistribution[], 2], {x, 0, 1, 0.001}];
plot = ListPlot[manifold, PlotStyle -> Orange]Out[1]=
创建一个具有“瓶颈”层的网络以学习流形的参数化.
In[2]:=
net = NetChain[{25, Ramp, 1, 25, Ramp, 2}, "Input" -> 2]Out[2]=

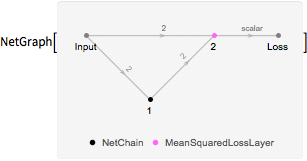
创建一个损失网络,根据“重构误差”来计算损失. “重构误差”是对网络在多大程度上能够产生一个和输入完全等同的输出输出的度量.
In[3]:=
lossNet =
NetGraph[{net, MeanSquaredLossLayer[]}, {1 -> 2,
NetPort["Input"] -> NetPort[2, "Target"]}]Out[3]=
在流形上训练损失网络并从损失网络提取出原始网络.
In[4]:=
lossNet =
NetTrain[lossNet, <|"Input" -> manifold|>, BatchSize -> 4096];
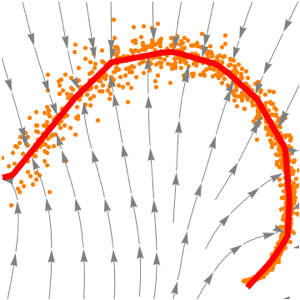
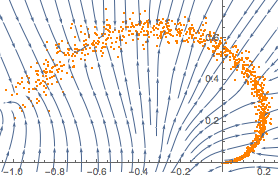
trained = NetExtract[lossNet, 1];图示网络如何将任意的点投影到流形上.
In[5]:=
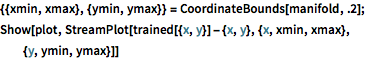
{{xmin, xmax}, {ymin, ymax}} = CoordinateBounds[manifold, .2];
Show[plot,
StreamPlot[
trained[{x, y}] - {x, y}, {x, xmin, xmax}, {y, ymin, ymax}]]Out[5]=
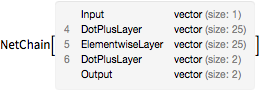
将网络拆分成一个“编码器”和“解码器”网络(“编码器”用单个标量值将点参数化,而“解码器”则从该参数化重构点).
In[6]:=
decoder = Drop[trained, 3]
encoder = Take[trained, 3]Out[6]=
Out[6]=
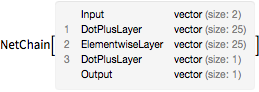
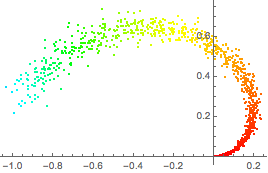
对原始流形上的每个点,按照其在编码器下的参数化着色.
In[7]:=
ListPlot[Style[#, Hue[First[0.3 + encoder[#]]/3]] & /@ manifold]Out[7]=
将编码器用于流形来获取参数的范围.
In[8]:=
{min, max} = MinMax[encoder[manifold]]Out[8]=
连同原始流形显示在这个范围内的重构.
In[9]:=
Show[plot, ListLinePlot[Table[decoder[x], {x, min, max, .01}]]]Out[9]=