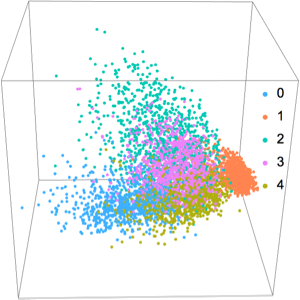
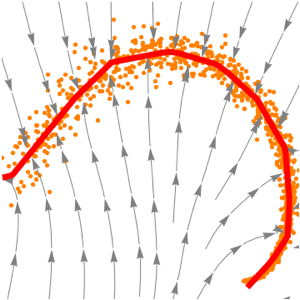
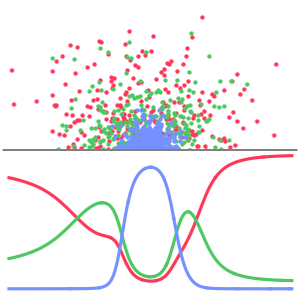
멀티태스킹 학습
CIFAR-100 데이터 집합의 이미지 라벨과 하위 라벨을 분류하는 합성곱 네트워크를 훈련합니다.
훈련 데이터 집합을 취득합니다.
In[1]:=

obj = ResourceObject["CIFAR-100"];
trainingData = ResourceData[obj, "TrainingDataset"];
RandomSample[trainingData, 5]Out[1]=

이미지의 라벨 및 하위 라벨을 취득합니다.
In[2]:=
labels = Union@Normal@trainingData[All, "Label"]
sublabels = Union@Normal@trainingData[All, "SubLabel"]Out[2]=
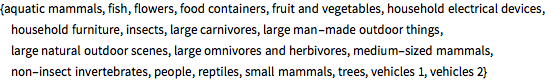
Out[2]=

간단한 합성곱 네트워크를 정의합니다.
In[3]:=

convnet = NetChain[{
ConvolutionLayer[20, {5, 5}],
ElementwiseLayer[Ramp],
PoolingLayer[{2, 2}, {2, 2}],
ConvolutionLayer[50, {5, 5}],
ElementwiseLayer[Ramp],
PoolingLayer[{2, 2}, {2, 2}],
FlattenLayer[],
DotPlusLayer[500],
ElementwiseLayer[Ramp]
}, "Input" -> NetEncoder[{"Image", {32, 32}}]]Out[3]=

라벨 및 하위 라벨의 예측을 실시하여 합성곱 네트워크의 결과를 사용하는 네트워크를 생성합니다.
In[4]:=

net = NetGraph[{convnet, 100, SoftmaxLayer[], 20,
SoftmaxLayer[]}, {NetPort["Image"] ->
1 -> 2 -> 3 -> NetPort["SubLabel"],
2 -> 4 -> 5 -> NetPort["Label"]},
"Label" -> NetDecoder[{"Class", labels}],
"SubLabel" -> NetDecoder[{"Class", sublabels}]]Out[4]=
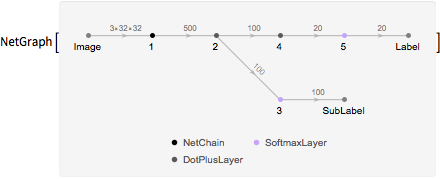
네트워크를 훈련하고 두 출력에 교차 엔트로피의 손실 함수 추가를 NetTrain이 자동으로 취합니다.
In[5]:=
net = NetTrain[net, trainingData]Out[6]=
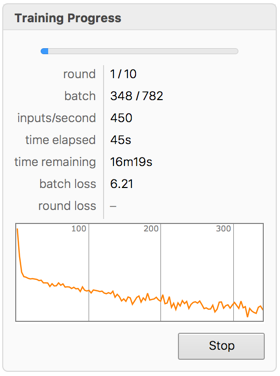
이미지를 분류하고 라벨과 하위 라벨 모두를 얻습니다.
In[7]:=
net[\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJwtlHdQ01m7x3fu/ePdO2/ZdS1Ib2mUBAgQSiAJpAEJJJBiCkkgIYQUEtIo
BiT0qlIV1EXFq+jrYlvLigUVkVVYZFdZ6wICFooiAlJC8rt5Z+7M95x5zvnj
Oef5zme+nmJNSuZ/ffPNN/pv7VtKel6MTpdewPjefmCp9XKZWpoRrzZIZVJd
uPi/7Zce/7/+U8+uAR/XgM9rtg8rm+9WrLMrts9rwLIVmF8HJhetYwvA60/A
C7sWgdHPwB8fgZE5YGQWeDwDDM8Av723DEyu908Dd6aB25PArXGgZwy4+hq4
9Ao49xL46Tnw71FgcgmYWtycXbXNfLVNL1omP2+8XbS8W7a+ml//8+3Sszfz
zyfnX8+tvZy3Pp0Ffp+zjczYnnwAfp+2DI59ujYw3H37wcDrxQcTtrvjttvj
mzfGrNdeWy+/sl18aTv/3PbTqO3tMjC1sD6zZFlYtc4vb84uW959WZtaWL39
8I+T3ZeaDrQeO9HRN/Tb2Nzqi4/A04+Wp3OWP99v9j+ZPvpTd1tHa+uhlku9
94fGVwbebN57Y+mdsNwc37w+Zr3yl/XnV9aLL2x2cz593Vxc21z5urG6alnd
sK5YgXdzs11dJ5qbalVKYUFBVmW9eWDk2bOZldGF5ecfV+6OjHVdvF7fUtXc
uKe1qbSpff+V+48eTSwNfrAOvLfdmbTemLD8Mr559S/rlVd2t61LG9Y1AFi3
bC5/WVpfW19b25iaeN26t6SiWFNSpCgxqxRKQWNTfdeFS3+8+/Rs9uvZqz0H
DjfW1JvKzDl11caikpzSuqrua3eHXs0Nz1j73lp7JzduTVhvjtt6XgOf162f
Vi2fN6wLK+tDI0+GRx733rnZdaK9pd602yjW5wjy8zIKTSpJ+q4MhbL/6ZvR
d8vtnZ2V1fkGvTRLyskzSvTGzDRp2p6K+u4bj/onVn79APRNrd+dtPVOALfG
7PDY5lYssyuWua+2Y2cuFJaaq+vNlRX6/TXGipJsnVaYKWOpsgW8VBaVwa1s
On7/yfjJ7u5Ck9aoy0wTJOYaxCq1mMllMtMza4+ev/NyvufPmYG36/1vbX1T
tntvgLk1wE7mzFernZ/jZ382lRQXFuWUlWi06lQ+N0GnlzHZFBQKgcbhCFQm
ky81Ve3b19xabMpVy4UVJZpcg4SaSPKGgcJi8XnV+6rbO8sOnb794uOvby0D
05aBKevcOvDhq82u+TVg6OmLtvZ2dVZ6Xk5GEhWLCoWz2Ux/f/gPW7Z7QBAR
MXFRMbHRJDKHL5QIUnOyRJWlaqWcA0f4eEFBkbFoiVysyTNIDMUnekcfvlsf
fG959M46vwHMrG7OrtmmF5Z6em83N9Vly0VcVnwCOSochUSFhoWiIqG+cHdw
gAc4wBvmExIVliri81n0st26AqMshUklkMmJdIpCwSkrz+FIJFiOovzk7aH3
GyOz1gcTywubdoss8+vWD19WOk92ZmZw2ex4Mjmanhgrz+IxmfQMqTw+iQbx
Re5w8nJwcQsICaIlUzPSOTWludQ4HNjHB4MnpqVxqsuU5WVqQgoHw9Pl7Ou6
9OjZ4NTMhYfDXzaBhTXrFwvwfHyy6/RJjTJdJEhJF/JFfEZNbY4hVyaWKHB4
spsn2D8wCOIHc3B2dXJxhYDdC3LlAl5KSCgqAh2VId7VWGfMVgjQeGpYvIin
Lt3b2XXx13sdV39asgALq5t29Q8+7DjasreqQCXjc9l0RSZfb+ASyMh4ShwE
BkFHR1CTEnz9/bZtd9q6zcHdw53JTOKwkwtNhWw2m8+Jry5VUSkkn6CoYFxy
qiK/qfP0hXu3jl8583UTWN6wvZ9fPHPu1IED5ub63D35Mqk4Wa8VJVIxBFJI
lootlXFlcl5ICAIG8QeBYS6u7g6Ort4QP7A3SKfR5mjUxhyhuVCWQKchMRQq
V8YQSasPNJ+/c+7ElcPrNuDTl6X+B30XL3dWVekNGuFug9ioSzPoBJJ0Wn5+
hlSWQmMSY/ARzs6OTi4ebu4eYAjExcMbiYr19w2ORmPUWmlDnS5XKyAmECks
HjIaDwoKMNXlH7vY2Ha6xAoA858/nuk61NhgytHImMlxxQWyLDErMyPFXCwx
aAUJcbHuIC9fXzgaHeMJ9v1hyw5nZ2cX+yu+IVCfIBw+XpeX1bI/p6Faa58x
GhftiwwVa1THL3V0dDc0HzPb+y+tLt/qOZetFMSRCbxdlKZ9uUatJDEhZheL
hMeFQcFgLwgY4Q+PI8V5evt4g3ycnd12Ork4OLtDA+DynAJVtmp/jbKmND2Z
gUNjo5JYwvqDP9a21bR1tTQfa7IAwJpl7dnoQ71WGhQI57BIe3ansVLIIchA
Px+Im4vrtq07COQoHjdeImZ6gd1dPUE/bHcCQ2EpTJpCK207dKSxrurAXm1N
mZTBIvgFIIjUXew0BSON03Ts4Kkrl+3/t9gsczN/lZi1DAZFmyMQcPCRqEAo
DOzk5OTh7g2HB2CxEQW5mVwm2d3Nzdkd4uoJ2+6wE08IN+9R7SvLO91e3NFs
1KpSiaQoDy8wAoV1BPkFR2PLGxtOXbvRc/fXv6beDg3e6+ps3FuTr9NwM4Q0
Is4eA0QCgQTz8fHyggbCg1WyTGJsLAjkh4rEhIZjvEFQOAIiEVAaSxQde5UG
OYMYg4HBYFAfBJGSHBIdGxWX0NRx5PztG/K8mpPd15+NjnQeLG+t1ZUVZaUy
KbhIVBw5js3mxcRg/WCBBGwsn8OjJNJ8AwJJceTEpGR0FN4fESTgJ5l0fJMm
lcugJFASEUEoNBbPYPODw9FkBr2gvLjlaOsumXG3uerc6SPNVXqzPk2XyU5j
JSPhflFojEiYQaVS6TSWSinF47HBwSGhYZGxeHJkJB6LjYfC4AEBCH8YKJ4Y
QyKTMuRKvkgcEIwCwfz8AoLik2nk5ESGiEdmCtQGg1GdurdEWZUvNYiZ6vRU
KpnEZvGkGSoikazV5O8xm4KCEBgMls8T6g27xWKVQmHg8vlgMAwZjCYm0NNk
2SGRGHhQMNjH93/++a/tjo6oiHAPkHc0AYdERzJ5bHkWq7wovb1a/WOFrkSf
lUCOwWFJaUK5vWFdbVtxSV3BbnNKMguLxiCDQu15SaOn7OKliMUcjVaLwpLi
aLtCw6OCw0LD0JGuHu6BIcHRGBwmKqIoL1uVnY4MRVCTcDnZrKYK5cEyjUEh
wESHh6EwdBo3GhNTXr6/41i3yVTB54lCkEgXN9dtDtsDgxHpGRxaUmyqkJdn
rrAzHxKOcfXydPb0CAoPDQwLE4rlnT8evn/t7IWztRmiRDwukMMgqiWsTE4C
kxITR8DFYnFRURGIIFhpZZHJVEAgkINDw+BIRAQm0hPiERiCiCXgvbxAYIhP
anqWylCUKlEggkO3OOyEIZFJPN7lGzenx54uTv9+6piptlyhUbIlnEQ+EaNM
IWfSiQxilIhLk0rYaLSfUsXPN2oYdDoYDIL5g2OJOH8E1A8OCwgM/g+lAQH2
3BZJs079+3RzSz2BFBMaGSnJkp2/cOTWL4fvXD9448LRg3vLuDQqnUAoUatO
1FVUa5Qiavyh+uozHe0UAmZPvu5M5+H25gYOKzk+DoOOhApEZL4wITgcHhIW
AoJ4OzjtgPpCCwpyThxv0uvk0dFRoWEoiZyfkc3nSBLn39wd7DtZW6reV2ns
aqvo6Wy+duRAXprwt5u/vBx8KKTTfz59avj+9VNHWo1qmUrGKcwX1VQpOHy8
g+v3UH9fJxe3v337t3/+/Vsvd0e4n7eHh5OTi6OblzskAAYLDwwlo578Vvp0
pGL094bRgabXd5qnbx568r9N+7MELbs1LUWGGH+IIB4vpJFIkShidBg9HiPi
UIS8JBDI5du//+OH7S47HT22fL9t63dbtn73r21bvw9C+tAYJBaXrDNw8ovT
247m9t0zP35Y92Lk4Iu+5ueXG4aPV/ZW5p3MkZXzmVoKXhQVIsJG4P39Ed5e
vmBPONTb29MFCgU7Ou3cuuM7VzdHKMTT3887PNyfz4szFwnPnS2+1VN+/Wrh
/d6y+3fLBgeqtQWswmJhqVlUVCDQK1kaEcUkYdZq+I25/P16TletuqMkKz8z
SSqIFfAwHFZEKg+TJiSmC4nZKkpFGa+5Udp2IKvrlLG/v+Hx46bHw1XDQ+an
I9UjQ9WPHpQN9Jn/D3Y/x6I=
"], {{0, 32}, {32, 0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{32, 32},
PlotRange->{{0, 32}, {0, 32}}]\)]Out[7]=
"SubLabel" 출력에 가장 알맞는 분류를 취득합니다.
In[8]:=
net[\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJwtlHdQ01m7x3fu/ePdO2/ZdS1Ib2mUBAgQSiAJpAEJJJBiCkkgIYQUEtIo
BiT0qlIV1EXFq+jrYlvLigUVkVVYZFdZ6wICFooiAlJC8rt5Z+7M95x5zvnj
Oef5zme+nmJNSuZ/ffPNN/pv7VtKel6MTpdewPjefmCp9XKZWpoRrzZIZVJd
uPi/7Zce/7/+U8+uAR/XgM9rtg8rm+9WrLMrts9rwLIVmF8HJhetYwvA60/A
C7sWgdHPwB8fgZE5YGQWeDwDDM8Av723DEyu908Dd6aB25PArXGgZwy4+hq4
9Ao49xL46Tnw71FgcgmYWtycXbXNfLVNL1omP2+8XbS8W7a+ml//8+3Sszfz
zyfnX8+tvZy3Pp0Ffp+zjczYnnwAfp+2DI59ujYw3H37wcDrxQcTtrvjttvj
mzfGrNdeWy+/sl18aTv/3PbTqO3tMjC1sD6zZFlYtc4vb84uW959WZtaWL39
8I+T3ZeaDrQeO9HRN/Tb2Nzqi4/A04+Wp3OWP99v9j+ZPvpTd1tHa+uhlku9
94fGVwbebN57Y+mdsNwc37w+Zr3yl/XnV9aLL2x2cz593Vxc21z5urG6alnd
sK5YgXdzs11dJ5qbalVKYUFBVmW9eWDk2bOZldGF5ecfV+6OjHVdvF7fUtXc
uKe1qbSpff+V+48eTSwNfrAOvLfdmbTemLD8Mr559S/rlVd2t61LG9Y1AFi3
bC5/WVpfW19b25iaeN26t6SiWFNSpCgxqxRKQWNTfdeFS3+8+/Rs9uvZqz0H
DjfW1JvKzDl11caikpzSuqrua3eHXs0Nz1j73lp7JzduTVhvjtt6XgOf162f
Vi2fN6wLK+tDI0+GRx733rnZdaK9pd602yjW5wjy8zIKTSpJ+q4MhbL/6ZvR
d8vtnZ2V1fkGvTRLyskzSvTGzDRp2p6K+u4bj/onVn79APRNrd+dtPVOALfG
7PDY5lYssyuWua+2Y2cuFJaaq+vNlRX6/TXGipJsnVaYKWOpsgW8VBaVwa1s
On7/yfjJ7u5Ck9aoy0wTJOYaxCq1mMllMtMza4+ev/NyvufPmYG36/1vbX1T
tntvgLk1wE7mzFernZ/jZ382lRQXFuWUlWi06lQ+N0GnlzHZFBQKgcbhCFQm
ky81Ve3b19xabMpVy4UVJZpcg4SaSPKGgcJi8XnV+6rbO8sOnb794uOvby0D
05aBKevcOvDhq82u+TVg6OmLtvZ2dVZ6Xk5GEhWLCoWz2Ux/f/gPW7Z7QBAR
MXFRMbHRJDKHL5QIUnOyRJWlaqWcA0f4eEFBkbFoiVysyTNIDMUnekcfvlsf
fG959M46vwHMrG7OrtmmF5Z6em83N9Vly0VcVnwCOSochUSFhoWiIqG+cHdw
gAc4wBvmExIVliri81n0st26AqMshUklkMmJdIpCwSkrz+FIJFiOovzk7aH3
GyOz1gcTywubdoss8+vWD19WOk92ZmZw2ex4Mjmanhgrz+IxmfQMqTw+iQbx
Re5w8nJwcQsICaIlUzPSOTWludQ4HNjHB4MnpqVxqsuU5WVqQgoHw9Pl7Ou6
9OjZ4NTMhYfDXzaBhTXrFwvwfHyy6/RJjTJdJEhJF/JFfEZNbY4hVyaWKHB4
spsn2D8wCOIHc3B2dXJxhYDdC3LlAl5KSCgqAh2VId7VWGfMVgjQeGpYvIin
Lt3b2XXx13sdV39asgALq5t29Q8+7DjasreqQCXjc9l0RSZfb+ASyMh4ShwE
BkFHR1CTEnz9/bZtd9q6zcHdw53JTOKwkwtNhWw2m8+Jry5VUSkkn6CoYFxy
qiK/qfP0hXu3jl8583UTWN6wvZ9fPHPu1IED5ub63D35Mqk4Wa8VJVIxBFJI
lootlXFlcl5ICAIG8QeBYS6u7g6Ort4QP7A3SKfR5mjUxhyhuVCWQKchMRQq
V8YQSasPNJ+/c+7ElcPrNuDTl6X+B30XL3dWVekNGuFug9ioSzPoBJJ0Wn5+
hlSWQmMSY/ARzs6OTi4ebu4eYAjExcMbiYr19w2ORmPUWmlDnS5XKyAmECks
HjIaDwoKMNXlH7vY2Ha6xAoA858/nuk61NhgytHImMlxxQWyLDErMyPFXCwx
aAUJcbHuIC9fXzgaHeMJ9v1hyw5nZ2cX+yu+IVCfIBw+XpeX1bI/p6Faa58x
GhftiwwVa1THL3V0dDc0HzPb+y+tLt/qOZetFMSRCbxdlKZ9uUatJDEhZheL
hMeFQcFgLwgY4Q+PI8V5evt4g3ycnd12Ork4OLtDA+DynAJVtmp/jbKmND2Z
gUNjo5JYwvqDP9a21bR1tTQfa7IAwJpl7dnoQ71WGhQI57BIe3ansVLIIchA
Px+Im4vrtq07COQoHjdeImZ6gd1dPUE/bHcCQ2EpTJpCK207dKSxrurAXm1N
mZTBIvgFIIjUXew0BSON03Ts4Kkrl+3/t9gsczN/lZi1DAZFmyMQcPCRqEAo
DOzk5OTh7g2HB2CxEQW5mVwm2d3Nzdkd4uoJ2+6wE08IN+9R7SvLO91e3NFs
1KpSiaQoDy8wAoV1BPkFR2PLGxtOXbvRc/fXv6beDg3e6+ps3FuTr9NwM4Q0
Is4eA0QCgQTz8fHyggbCg1WyTGJsLAjkh4rEhIZjvEFQOAIiEVAaSxQde5UG
OYMYg4HBYFAfBJGSHBIdGxWX0NRx5PztG/K8mpPd15+NjnQeLG+t1ZUVZaUy
KbhIVBw5js3mxcRg/WCBBGwsn8OjJNJ8AwJJceTEpGR0FN4fESTgJ5l0fJMm
lcugJFASEUEoNBbPYPODw9FkBr2gvLjlaOsumXG3uerc6SPNVXqzPk2XyU5j
JSPhflFojEiYQaVS6TSWSinF47HBwSGhYZGxeHJkJB6LjYfC4AEBCH8YKJ4Y
QyKTMuRKvkgcEIwCwfz8AoLik2nk5ESGiEdmCtQGg1GdurdEWZUvNYiZ6vRU
KpnEZvGkGSoikazV5O8xm4KCEBgMls8T6g27xWKVQmHg8vlgMAwZjCYm0NNk
2SGRGHhQMNjH93/++a/tjo6oiHAPkHc0AYdERzJ5bHkWq7wovb1a/WOFrkSf
lUCOwWFJaUK5vWFdbVtxSV3BbnNKMguLxiCDQu15SaOn7OKliMUcjVaLwpLi
aLtCw6OCw0LD0JGuHu6BIcHRGBwmKqIoL1uVnY4MRVCTcDnZrKYK5cEyjUEh
wESHh6EwdBo3GhNTXr6/41i3yVTB54lCkEgXN9dtDtsDgxHpGRxaUmyqkJdn
rrAzHxKOcfXydPb0CAoPDQwLE4rlnT8evn/t7IWztRmiRDwukMMgqiWsTE4C
kxITR8DFYnFRURGIIFhpZZHJVEAgkINDw+BIRAQm0hPiERiCiCXgvbxAYIhP
anqWylCUKlEggkO3OOyEIZFJPN7lGzenx54uTv9+6piptlyhUbIlnEQ+EaNM
IWfSiQxilIhLk0rYaLSfUsXPN2oYdDoYDIL5g2OJOH8E1A8OCwgM/g+lAQH2
3BZJs079+3RzSz2BFBMaGSnJkp2/cOTWL4fvXD9448LRg3vLuDQqnUAoUatO
1FVUa5Qiavyh+uozHe0UAmZPvu5M5+H25gYOKzk+DoOOhApEZL4wITgcHhIW
AoJ4OzjtgPpCCwpyThxv0uvk0dFRoWEoiZyfkc3nSBLn39wd7DtZW6reV2ns
aqvo6Wy+duRAXprwt5u/vBx8KKTTfz59avj+9VNHWo1qmUrGKcwX1VQpOHy8
g+v3UH9fJxe3v337t3/+/Vsvd0e4n7eHh5OTi6OblzskAAYLDwwlo578Vvp0
pGL094bRgabXd5qnbx568r9N+7MELbs1LUWGGH+IIB4vpJFIkShidBg9HiPi
UIS8JBDI5du//+OH7S47HT22fL9t63dbtn73r21bvw9C+tAYJBaXrDNw8ovT
247m9t0zP35Y92Lk4Iu+5ueXG4aPV/ZW5p3MkZXzmVoKXhQVIsJG4P39Ed5e
vmBPONTb29MFCgU7Ou3cuuM7VzdHKMTT3887PNyfz4szFwnPnS2+1VN+/Wrh
/d6y+3fLBgeqtQWswmJhqVlUVCDQK1kaEcUkYdZq+I25/P16TletuqMkKz8z
SSqIFfAwHFZEKg+TJiSmC4nZKkpFGa+5Udp2IKvrlLG/v+Hx46bHw1XDQ+an
I9UjQ9WPHpQN9Jn/D3Y/x6I=
"], {{0, 32}, {32, 0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{32, 32},
PlotRange->{{0, 32}, {0, 32}}]\), "SubLabel" -> "TopProbabilities"]Out[8]=