ジップの法則

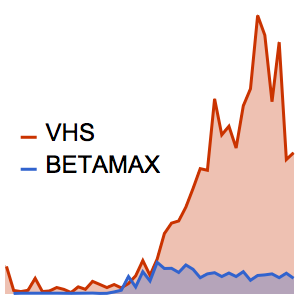
シップ(Zipf)の法則には，ある言語のコーパスにおける単語頻度は，頻度を降順でソートした後の大域的な単語リストにおけるその単語の順位に反比例するとある．例は，新関数のWordCountとWordCountsを使い，セルバンテスの小説「ドン・キホーテ」の単語集合でこの法則を示す．

ExampleDataにはドン・キホーテの第1巻のテキストがスペイン語で収録されている．

In[1]:=

textSpanish = ExampleData[{"Text", "DonQuixoteISpanish"}];

これから考察するサンプルには18万語以上の単語が含まれている．

In[2]:=

WordCount[textSpanish]

Out[2]=

異なるそれぞれの単語の数がWordCountsによって連想として与えられる．結果は数の降順でソートされている．

In[3]:=

association = WordCounts[textSpanish];

In[4]:=

Take[association, 10]

Out[4]=

最もよく使われる1,000語の頻度数を取り出す．

In[5]:=

counts = Take[Values@association, 1000];

ベキ法則を使ってこの数を近似する．そのために，線形フィットに使う対数を取る．ジップの法則によると，指数はほぼ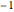でなければならないが，これに近い値が得られる．

In[6]:=

f[x_] = Fit[Log[Transpose[{Range[1000], counts}]], {1, x}, x]

Out[6]=

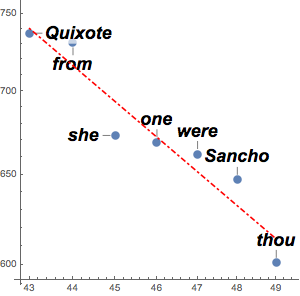
フィットを実際のデータとともに可視化する．

In[7]:=

Show[ ListLogLogPlot[counts, PlotStyle -> PointSize[0.02]], LogLogPlot[Exp[f[Log[x]]], {x, 1, 1000}, PlotStyle -> Directive[DotDashed, Red]], AspectRatio -> 1, PlotRange -> All ]

Out[7]=

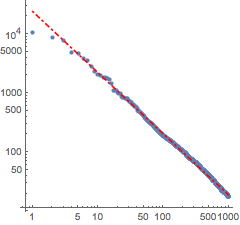
ジップの法則は任意の言語で成り立つので，同じ計算を英語版の「ドン・キホーテ」に対して行う．

In[8]:=

textEnglish = ExampleData[{"Text", "DonQuixoteIEnglish"}];

In[9]:=

associationEnglish = WordCounts[textEnglish]; countsEnglish = Take[Values@associationEnglish, 1000];

In[10]:=

Take[associationEnglish, 10]

Out[10]=

求まった指数は，ここでも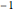に近い．

In[11]:=

Fit[Log[Transpose[{Range[1000], countsEnglish}]], {1, x}, x]

Out[11]=