Mega-Dichteplot
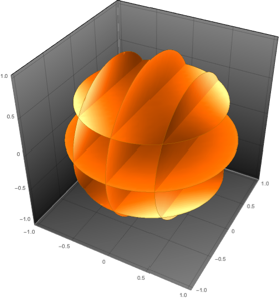
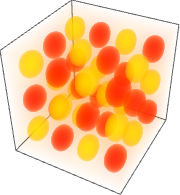
Erzeugen Sie den 3D-Dichteplot einer Funktion, wobei die Extremwerte am wenigsten transparent sind.
In[1]:=

density =
DensityPlot3D[
Sin[\[Pi] x] Sin[\[Pi] y] Sin[\[Pi] z], {x, -2, 2}, {y, -2,
1}, {z, -2, 1},
ColorFunction -> (Blend[{RGBColor[1, 0, 0], RGBColor[
1, 1, 0]}, #] &),
OpacityFunction -> Function[f, If[Abs[f] > .5, .22, .01]],
OpacityFunctionScaling -> False, PlotTheme -> "Minimal"]Out[1]=
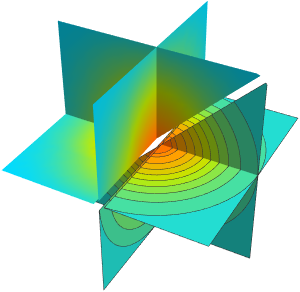
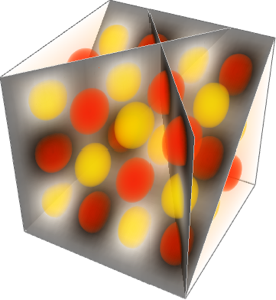
Plotten Sie dieselbe Funktion auf Querschnitte der Region.
In[2]:=

slices = SliceDensityPlot3D[
Sin[\[Pi] x] Sin[\[Pi] y] Sin[\[Pi] z], {z == y, x == y,
x == -y}, {x, -2, 2}, {y, -2, 1}, {z, -2, 1},
BoundaryStyle -> Directive[GrayLevel[1, .5], AbsoluteThickness[1]],
ColorFunction -> (Abs[#] &), PlotPoints -> 60,
PlotTheme -> "Minimal"]Out[2]=

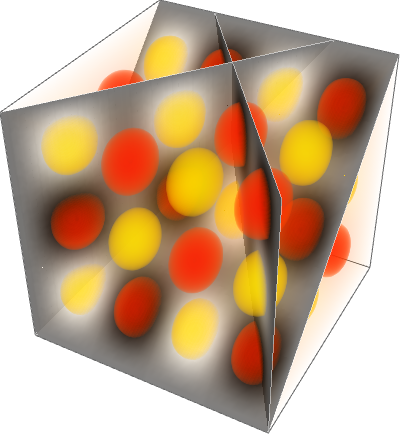
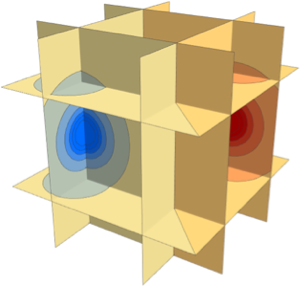
Kombinieren Sie die zwei Plots zu einem Mega-Dichteplot.
In[3]:=
Rasterize[Show[density, slices, ImageSize -> 400]]Out[3]=