Wolfram言語™

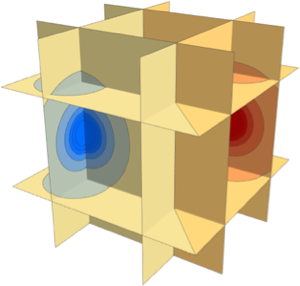
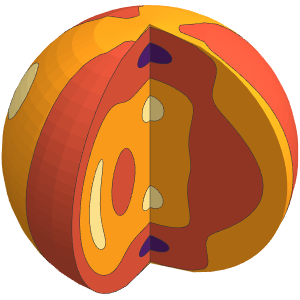
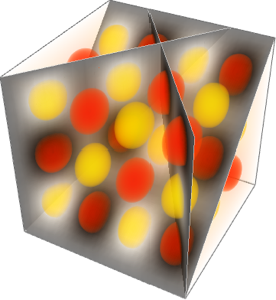
固有関数の可視化

3Dラプラス(Laplace)演算子を定義する．

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x, y, z], {x, y, z}];

同次ディリクレ(Dirichlet)境界条件を指定する．

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y, z] == 0, True];

球体内の最小固有値と固有関数を求める．

In[3]:=

\[CapitalOmega] = Ball[{0, 0, 0}, 2]; {vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y, z], {x, y, z} \[Element] \[CapitalOmega], 2];

In[4]:=

funs

Out[4]=

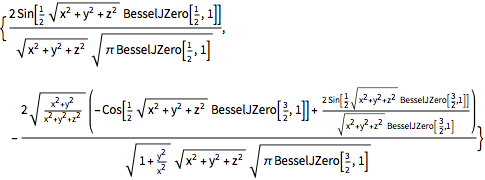
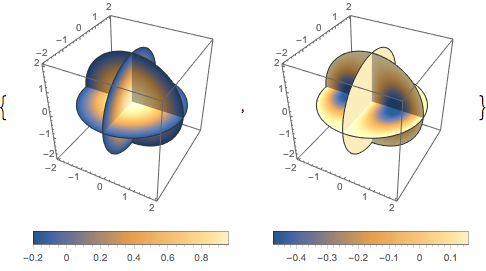
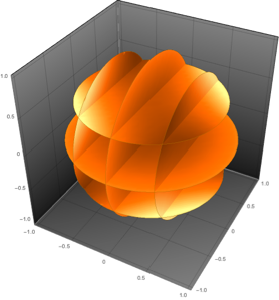
3D密度プロットを使って各固有関数をプロットする．

In[5]:=

Table[DensityPlot3D[ Evaluate[N[f]], {x, y, z} \[Element] \[CapitalOmega], PlotTheme -> "NoAxes", PlotLegends -> Placed[Automatic, Below]], {f, funs}]

Out[5]=

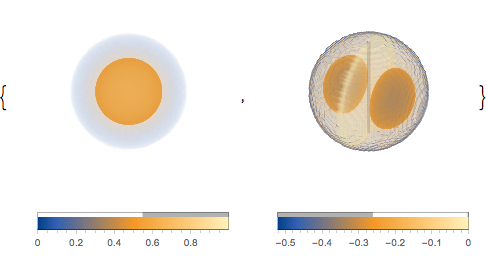
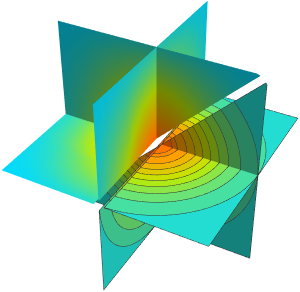
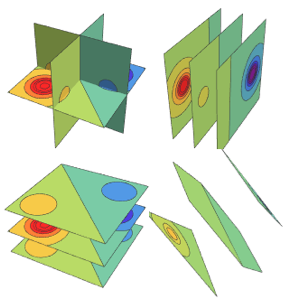
座標平面を使って密度をプロットする：

In[6]:=

Table[SliceDensityPlot3D[ Evaluate[N[f]], {x, y, z} \[Element] \[CapitalOmega], PlotLegends -> Placed[Automatic, Below]], {f, funs}]

Out[6]=