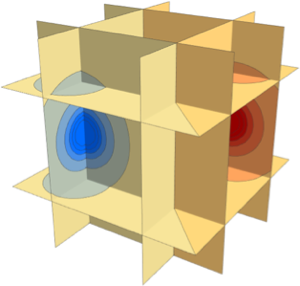
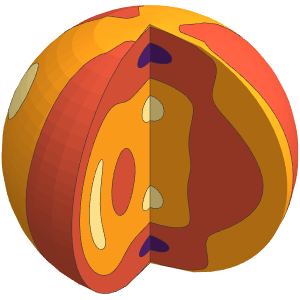
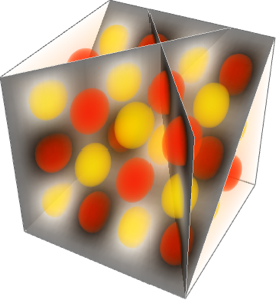
可视化特征函数
定义一个三维拉普拉斯算子.
In[1]:=
\[ScriptCapitalL] = -Laplacian[u[x, y, z], {x, y, z}];设定齐次狄利克雷边界条件.
In[2]:=
\[ScriptCapitalB] = DirichletCondition[u[x, y, z] == 0, True];找出一个球内的最小特征值和特征函数.
In[3]:=
\[CapitalOmega] = Ball[{0, 0, 0}, 2];
{vals, funs} =
DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]},
u[x, y, z], {x, y, z} \[Element] \[CapitalOmega], 2];In[4]:=
funsOut[4]=
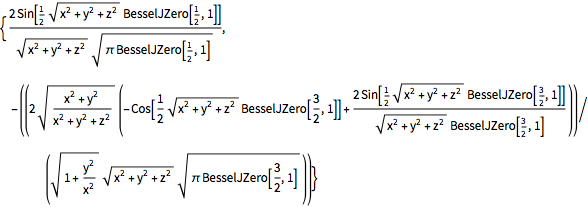
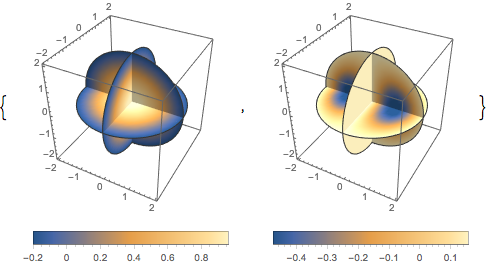
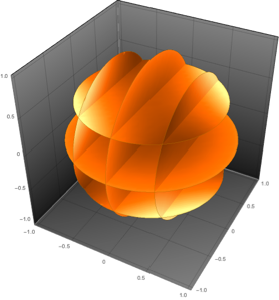
用三维密度图绘制每一本征函数.
In[5]:=
Table[DensityPlot3D[
Evaluate[N[f]], {x, y, z} \[Element] \[CapitalOmega],
PlotTheme -> "NoAxes", PlotLegends -> Placed[Automatic, Below]], {f,
funs}]Out[5]=
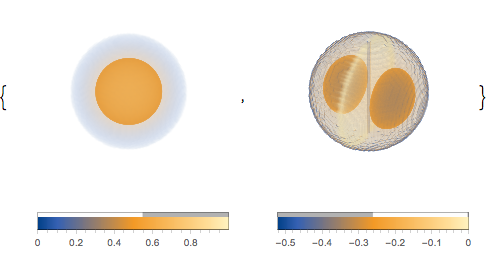
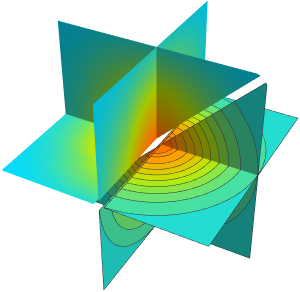
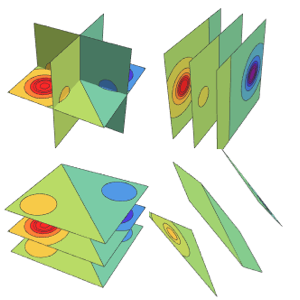
用坐标平面上绘制的密度.
In[6]:=
Table[SliceDensityPlot3D[
Evaluate[N[f]], {x, y, z} \[Element] \[CapitalOmega],
PlotLegends -> Placed[Automatic, Below]], {f, funs}]Out[6]=