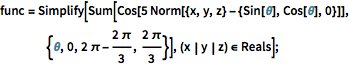可视化切片: Wolfram语言 11 的新功能

可视化切片

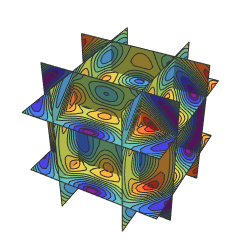
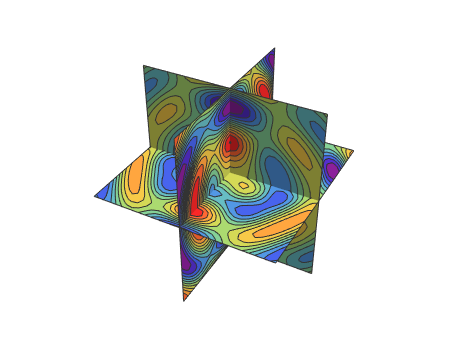
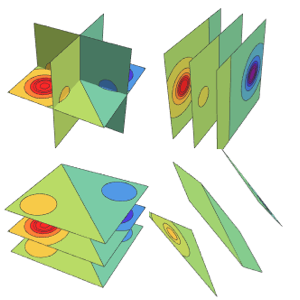
用多个相交平面作为表面，在其上绘制函数的等值线图.

显示完整的 Wolfram 语言输入

In[1]:=

opts = {ColorFunction -> ColorData[{"Rainbow", {-2.5, 2.5}}], 
   ColorFunctionScaling -> False, ClippingStyle -> Automatic, 
   PlotTheme -> "Bare", SphericalRegion -> True, ImageSize -> 250, 
   Contours -> Subdivide[-2.5, 2.5, 10]};

In[2]:=

func = Simplify[
   Sum[Cos[5 Norm[{x, y, z} - {Sin[\[Theta]], Cos[\[Theta]], 
         0}]], {\[Theta], 0, 2 \[Pi] - (2 \[Pi])/3, (2 \[Pi])/
     3}], (x | y | z) \[Element] Reals];

In[3]:=

With[{k = 1},
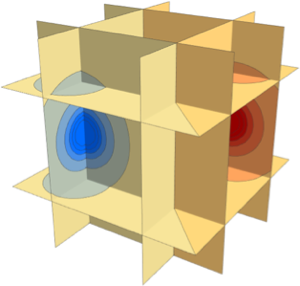
 SliceContourPlot3D[
  func, {x == -k, x == k, y == -k, y == k, z == -k, z == k}, {x, -2, 
   2}, {y, -2, 2}, {z, -2, 2}, Evaluate@opts]
 ]

Out[3]=

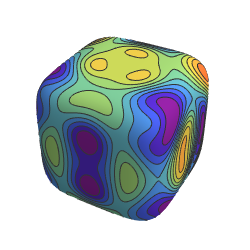
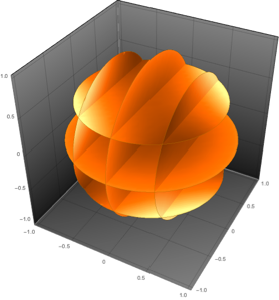
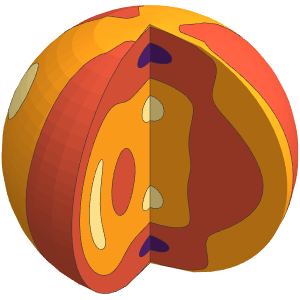
用一个p-范数球作为表面.

In[4]:=

With[{p = 5},
 SliceContourPlot3D[func, 
  BoundaryDiscretizeRegion[
   ImplicitRegion[
    Norm[{x, y, z}, p] <= 
     2, {{x, -2, 2}, {y, -2, 2}, {z, -2, 2}}], {{-2, 2}, {-2, 2}, {-2,
      2}}, MaxCellMeasure -> {"Length" -> 0.05}], {x, -2, 2}, {y, -2, 
   2}, {z, -2, 2}, Evaluate@opts]
 ]

Out[4]=

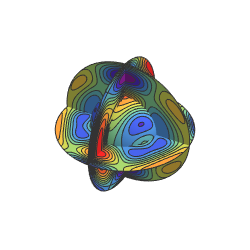
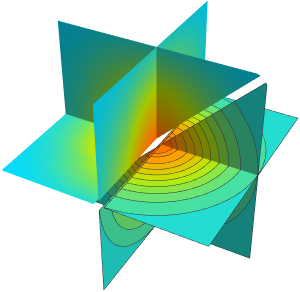
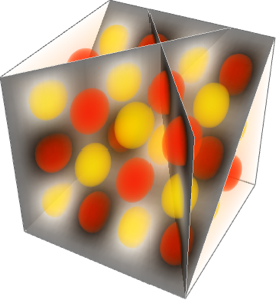
用一个球体以及与之相交的圆盘作为表面.

显示完整的 Wolfram 语言输入

In[5]:=

sphere = BoundaryDiscretizeRegion[
   ImplicitRegion[Norm[{x, y, z}, 2] <= 1,
    {{x, -2, 2}, {y, -2, 2}, {z, -2, 2}}], {{-2, 2}, {-2, 2}, {-2, 
     2}}, MaxCellMeasure -> {"Length" -> 0.05}];

In[6]:=

planes = With[{r = 2}, DiscretizeRegion[ImplicitRegion[
     (x^2 + y^2 <= r^2 && z == 0) || (x^2 + z^2 <= r^2 && 
        y == 0) || (z^2 + y^2 <= r^2 && x == 0),
     {{x, -2, 2}, {y, -2, 2}, {z, -2, 2}}], {{-2, 2}, {-2, 2}, {-2, 
      2}}, MaxCellMeasure -> {"Length" -> 0.05}]
   ];

In[7]:=

SliceContourPlot3D[func, {sphere, planes}, {x, -2, 2}, {y, -2, 
  2}, {z, -2, 2}, Evaluate@opts]

Out[7]=

从表面的不同参数设置之间的平滑过渡得到一个有趣的影片.

播放动画

停止播放动画

Wolfram 语言™

可视化切片

相关范例