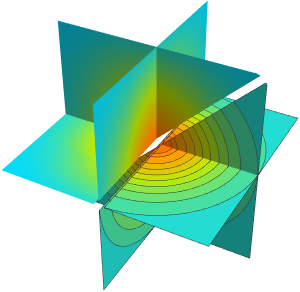
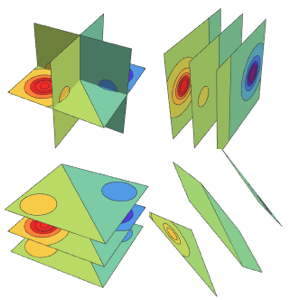
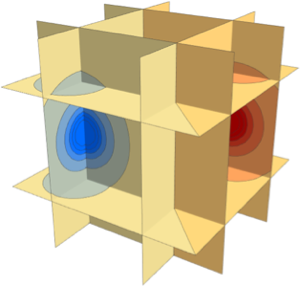
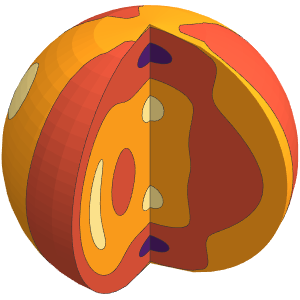
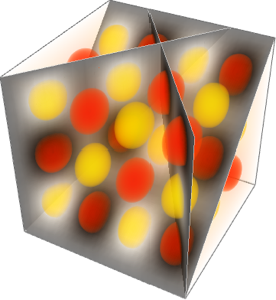
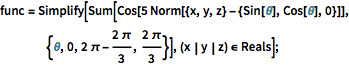Visualisez les coupes

Utilisez plusieurs plans d'intersection comme surfaces sur lesquelles tracer les contours d'une fonction.

In[1]:=

opts = {ColorFunction -> ColorData[{"Rainbow", {-2.5, 2.5}}], ColorFunctionScaling -> False, ClippingStyle -> Automatic, PlotTheme -> "Bare", SphericalRegion -> True, ImageSize -> 250, Contours -> Subdivide[-2.5, 2.5, 10]};

In[2]:=

func = Simplify[ Sum[Cos[5 Norm[{x, y, z} - {Sin[\[Theta]], Cos[\[Theta]], 0}]], {\[Theta], 0, 2 \[Pi] - (2 \[Pi])/3, (2 \[Pi])/ 3}], (x | y | z) \[Element] Reals];

In[3]:=

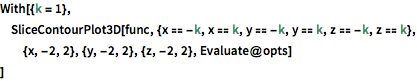
With[{k = 1}, SliceContourPlot3D[ func, {x == -k, x == k, y == -k, y == k, z == -k, z == k}, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Evaluate@opts] ]

Out[3]=

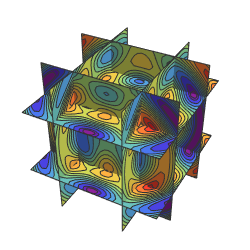
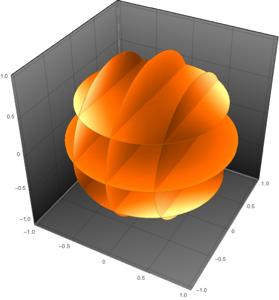
Utilisez une balle de norme 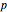comme surface.

In[4]:=

With[{p = 5}, SliceContourPlot3D[func, BoundaryDiscretizeRegion[ ImplicitRegion[ Norm[{x, y, z}, p] <= 2, {{x, -2, 2}, {y, -2, 2}, {z, -2, 2}}], {{-2, 2}, {-2, 2}, {-2, 2}}, MaxCellMeasure -> {"Length" -> 0.05}], {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Evaluate@opts] ]

Out[4]=

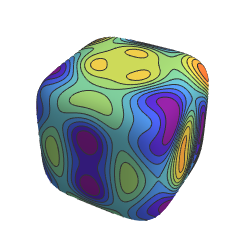
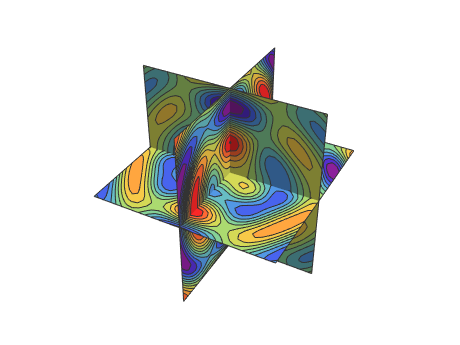
Utilisez une sphère et des disques croisant les surfaces.

In[5]:=

sphere = BoundaryDiscretizeRegion[ ImplicitRegion[Norm[{x, y, z}, 2] <= 1, {{x, -2, 2}, {y, -2, 2}, {z, -2, 2}}], {{-2, 2}, {-2, 2}, {-2, 2}}, MaxCellMeasure -> {"Length" -> 0.05}];

In[6]:=

planes = With[{r = 2}, DiscretizeRegion[ImplicitRegion[ (x^2 + y^2 <= r^2 && z == 0) || (x^2 + z^2 <= r^2 && y == 0) || (z^2 + y^2 <= r^2 && x == 0), {{x, -2, 2}, {y, -2, 2}, {z, -2, 2}}], {{-2, 2}, {-2, 2}, {-2, 2}}, MaxCellMeasure -> {"Length" -> 0.05}] ];

In[7]:=

SliceContourPlot3D[func, {sphere, planes}, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Evaluate@opts]

Out[7]=

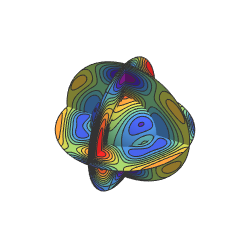
La transition entre les différents paramètres des surfaces se fait en douceur afin d'obtenir un film intéressant.

Jouer l'animation

Arrêter l'annimation