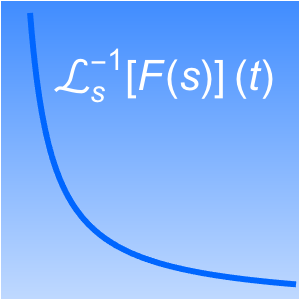
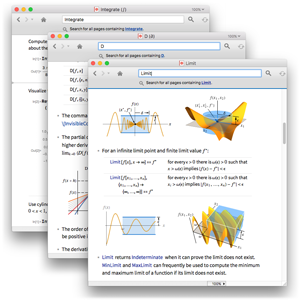
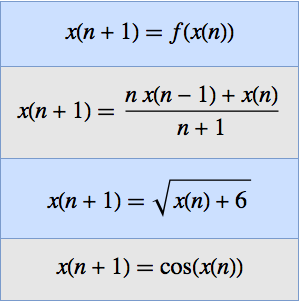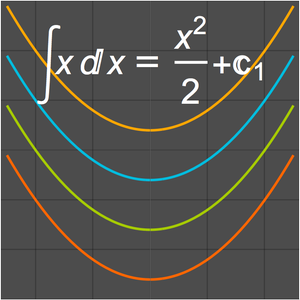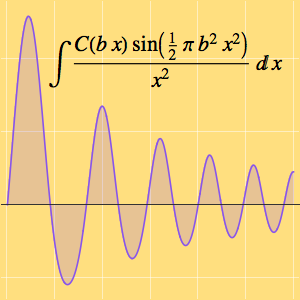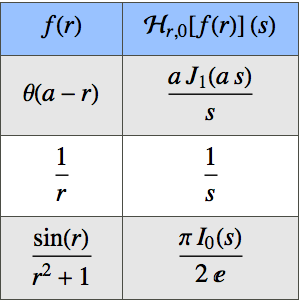Compute Limits of Multivariate Functions

A completely new limit feature is the support for multivariate and iterated limits. Multivariate limits are significantly harder to compute, and the Wolfram Language multivariate limit is the most powerful such limit functionality ever developed. See this blog post for 1000 further examples of its capabilities.

Compute the limit of the bivariate function at zero.

Visualize the result.

Here the limit is infinite.

Compute the limit at zero of a function that depends on a real symbolic parameter.

For positive 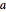, the limit is zero.

For non-positive , the limit does not exist.