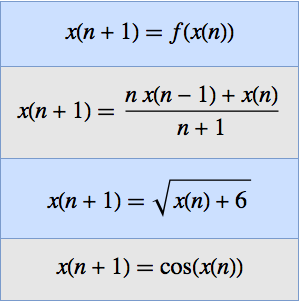Compute Klein's Invariant for an Elliptic Curve

The invariants of the Weierstrassian elliptic functions are standard concepts defined for elliptic curves. Version 12 provides functions for working directly with these invariants, as well as the half-periods and the values at half-periods of these elliptic functions.

WeierstrassE1, WeierstrassE2 and WeierstrassE3 give the values of WeierstrassP at the corresponding half-periods.

Similarly, WeierstrassEta1, WeierstrassEta2 and WeierstrassEta3 give the values of WeierstrassZeta at the corresponding half-periods.

Finally, WeierstrassInvariantG2 and WeierstrassInvariantG3 define the invariants for the Weierstrassian elliptic functions, which makes it convenient to use them in examples such as the one following.

Define the discriminant of the Weierstrass elliptic curve.

Compute the Klein j-invariant using the g-invariants for the curve.

Plot the imaginary part of the Klein invariant.

Compare with the built‐in function value.