O ciclo dos domingos de Páscoa ortodoxa
Usando a nova função FindRepeat, este exemplo mostrará que o padrão das datas da Páscoa ortodoxa se repete a cada 532 anos, e também identificará uma maneira simples de descobrir que um novo ciclo foi iniciado.
Para um determinado ano, essa função fornece o par {mês, dia} para o domingo de Páscoa ortodoxo.
Por exemplo, a Páscoa ortodoxa em 2019 cai no domingo, 15 de abril, no calendário juliano, que é domingo, 28 de abril, no calendário gregoriano.
A data da Páscoa no cristianismo ocidental é calculada com um algoritmo diferente e cai em 21 de abril de 2019. Veja este exemplo de cálculos compilados para uma análise das datas da Páscoa ocidental.
Calcule todas as datas da Páscoa ortodoxa no calendário juliano, do ano 1 ao ano 10000.
O resultado pode ser qualquer um dos 35 dias entre 22 de março e 25 de abril.
O ciclo das datas se repete a cada 532 anos.
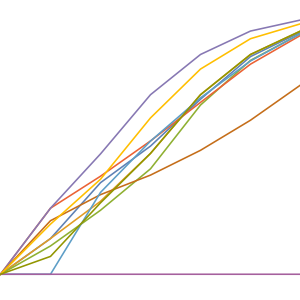
Esta é a distribuição de possibilidades para um único ciclo, movendo todas as datas para o mesmo ano, digamos 2000, para representação com DateHistogram.
Dois anos consecutivos nunca têm a mesma data para a Páscoa.
22 de março aparece quatro vezes no ciclo, por isso não pode ser usado para marcar o início de um ciclo. No entanto, em três ocasiões, será seguido pelo dia 11 de abril do ano seguinte e, em apenas uma ocasião, será seguido pelo dia 10 de abril.
Em seguida, você pode usar a sequência de 22 de março, 10 de abril, para definir uma noção do início de um novo ciclo. A função SequenceSplit encontrará esses pares, remova-os e separe os 10000 dias em sub-listas de comprimento 530.