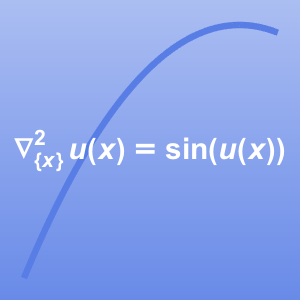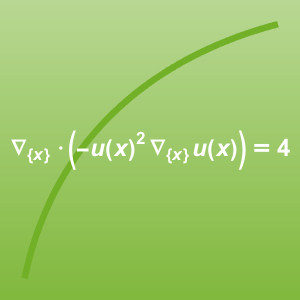Magnetostatics
To compute the torque of an electric motor, the magnetostatic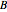 
field lines are computed. A Poisson-type equation 
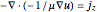is used as a model. Here, 
is the magnetic potential that is related to the magnetic field strength 
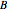and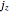 
is the current density in the 
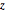direction.
The magnetic field strengths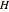 
and 
are related through 
. However, the permeability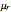 
is a function of the magnetic field 
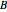itself. This makes the equation nonlinear. The 
curve data can be used to create a fit for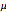 
.
Use two exponentials to fit the data.
Visualize the fit and the data.
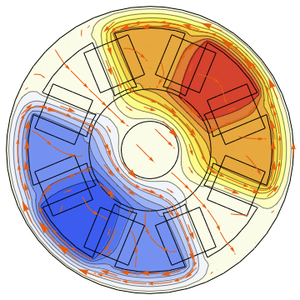
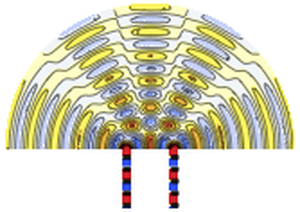
Import and visualize the geometry of the motor. In the following graphic, the stator is shown in gray and the rotor in red. The orange coil will carry a positive current, while the yellow coil will carry a negative current. The light orange coils will not carry a current.
A nonlinear Poisson-type equation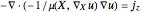 
is used as a model for the magnetostatics. The permeability 
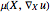is nonlinear and its values also differ in the different parts of the device.
The permeability depends on the intensity of the magnetic field.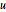 
in the 
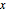and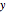 
directions is assumed to be zero. Thus the strength of the field is equal to the norm of the gradient of 
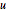. Set up the gradient of the magnetic field and avoid it becoming zero.
Specify a different permeability in different parts of the device.
Set up the current in the coils.
Solve the equation.
Visualize the magnetic potential and its gradient.
More details about this model can be found in the documentation.
