ベクトル解析と可視化
Wolfram言語では,n 次元のベクトルは長さ n のリストで表されます.
2つのベクトルのドット積を計算します:
| In[1]:= |
| Out[1]= |
外積の記号は,ESCcrossESCとタイプして入力します:
| In[2]:= |
| Out[2]= |
ベクトルのノルムを計算します:
| In[1]:= |
| Out[1]= |
ベクトルの x 軸上への投影を求めます:
| In[2]:= |
| Out[2]= |
2つのベクトル間の角度を求めます:
| In[3]:= |
| Out[3]= |
Wolfram言語には,ベクトル場の可視化に適した2Dと3Dの関数が含まれています:
| In[1]:= |
| Out[1]= | 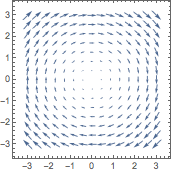 |
| In[2]:= |
| Out[2]= | 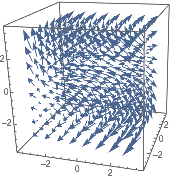 |
スライス面上にベクトル場をプロットします:
| In[3]:= |
| Out[3]= | 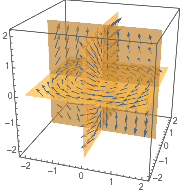 |
参照:ベクトル解析 »
参照:ベクトルの可視化 »
