Compute the Curvature of Curves in Any Dimensions 

ArcCurvature and FrenetSerretSystem compute curvatures for curves in any dimension.

ArcCurvature gives the single unsigned curvature.

In[1]:=

X Simplify[ArcCurvature[{r Cos[t], -r Sin[t]}, t], r > 0]

Out[1]=

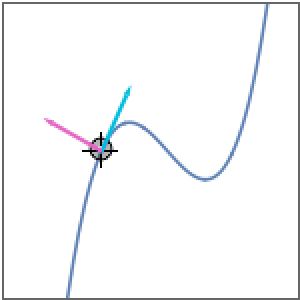
Curvature for a curve expressed in polar coordinates.

In[2]:=

X Simplify[ArcCurvature[{a t^2, t}, t, "Polar"], a > 0 && t > 0]

Out[2]=

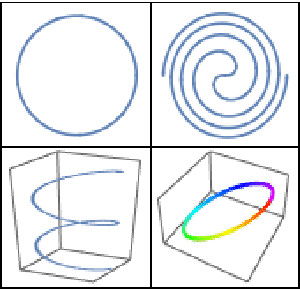
Curves in three and four dimensions.

In[3]:=

X Simplify[ArcCurvature[{r Cos[t], -r Sin[t], t}, t], r > 0]

Out[3]=

In[4]:=

X Simplify[ArcCurvature[{r Cos[t], -r Sin[t], Cos[t], Sin[t]}, t], r > 0]

Out[4]=

FrenetSerretSystem gives the generalized curvatures, which may be signed, and the associated basis.

In[5]:=

X Simplify[FrenetSerretSystem[{r Cos[t], -r Sin[t]}, t], r > 0]

Out[5]=

In three dimensions, the generalized curvatures are usually called curvature and torsion, and the associated Tangent/Normal/Binormal or TNB basis.

In[6]:=

X Simplify[FrenetSerretSystem[{r Cos[t], -r Sin[t], t}, t], r > 0]

Out[6]=

Visualize the four curves. The fourth dimension is represented by color.

show complete Wolfram Language inputhide input

In[7]:=

X Grid[{{ParametricPlot[{2 Cos[t], -2 Sin[t]}, {t, 0, 2 Pi}], PolarPlot[{2 Sqrt[t], - 2 Sqrt[t]}, {t, 0, 4 Pi}, PlotStyle -> ColorData[97, 1]]}, {ParametricPlot3D[{2 Cos[t], -2 Sin[t], t}, {t, 0, 4 Pi}, PlotTheme -> {"Default", "Scientific"}], ParametricPlot3D[{2 Cos[t], -2 Sin[t], Cos[t]}, {t, 0, 2 Pi}, ColorFunction -> (Hue[Sin[#4]] &), PlotTheme -> "Scientific"]}}, Dividers -> All]

Out[7]=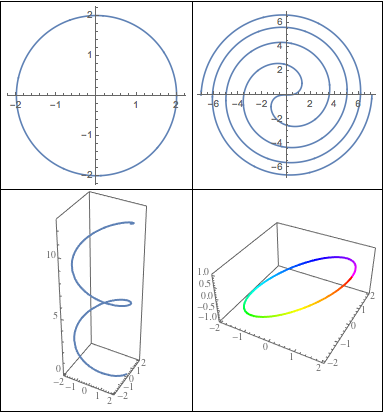