マリアナ海溝の標高を図にする
マリアナ海溝の位置を得る.
| In[1]:= | X |
| Out[1]= |
海溝の南北の断面をプロットする.
| In[2]:= | 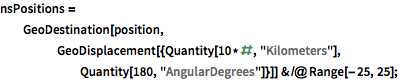 X |
| In[3]:= | X |
| In[4]:= |  X |
| Out[4]= |
海溝の東西の断面をプロットする.
| In[5]:= |  X |
| In[6]:= | X |
| In[7]:= |  X |
| Out[7]= |
海溝の起伏地図を作成し,断面図の位置に印を付ける.
| In[8]:= |  X |
| Out[8]= | 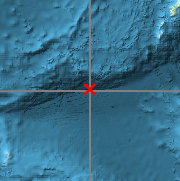 |
地図と断面図を組み合せる.
| In[9]:= | X |
| Out[9]= | 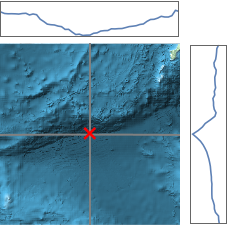 |
マリアナ海溝の位置を得る.
| In[1]:= | X |
| Out[1]= |
海溝の南北の断面をプロットする.
| In[2]:= | 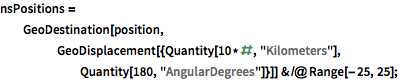 X |
| In[3]:= | X |
| In[4]:= |  X |
| Out[4]= |
海溝の東西の断面をプロットする.
| In[5]:= |  X |
| In[6]:= | X |
| In[7]:= |  X |
| Out[7]= |
海溝の起伏地図を作成し,断面図の位置に印を付ける.
| In[8]:= |  X |
| Out[8]= |  |
地図と断面図を組み合せる.
| In[9]:= | X |
| Out[9]= |  |
Questions? Comments? Contact a Wolfram expert »