Map an Arbitrary Function over a Time Series
TimeSeriesMap and TimeSeriesMapThread can be used to transform values of time series.
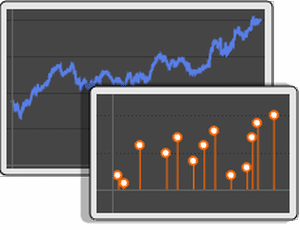
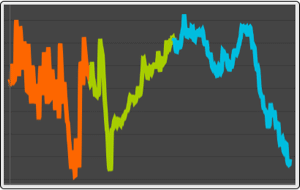
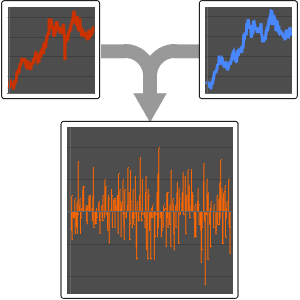
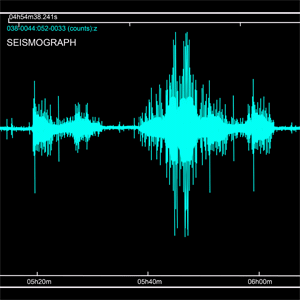
Time series of wind speeds in Champaign, IL in May 2014.
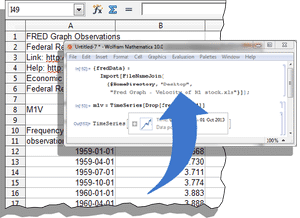
| In[1]:= | X |
| Out[1]= |
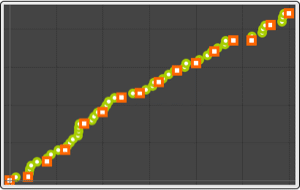
Use TimeSeriesMap to build the time series for the power output of a GE 1.5 MW wind turbine.
| In[3]:= | X |
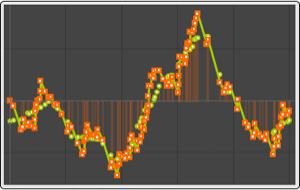
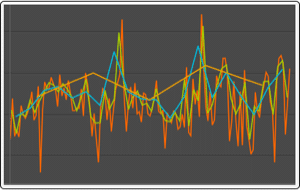
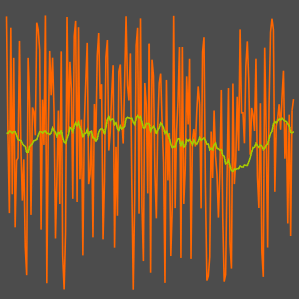
Visualize the daily moving average of the energy output.
| In[4]:= | X |
| Out[4]= |
| Out[5]= | 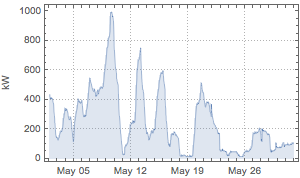 |
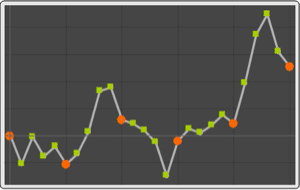
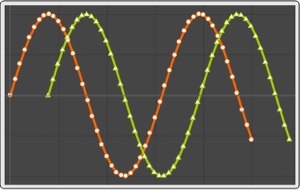
Use TimeSeriesMapThread when the transformation function requires access to the time-value pair.
| In[6]:= | X |
| In[7]:= | X |
| Out[7]= |
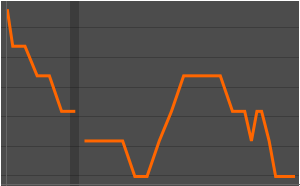
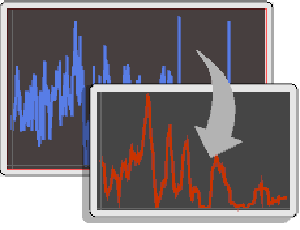
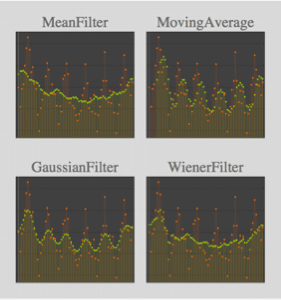
Find the model residuals.
| In[8]:= | X |
| Out[8]= |
| In[9]:= | X |
| Out[9]= | 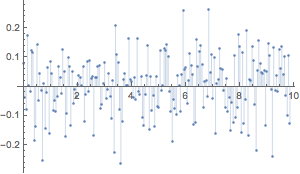 |