Numbers

Notes for Python programmers:
The Wolfram Client Library for Python natively supports many Python numeric types, including NumPy's integer, float16, etc.
The Wolfram Language by default does exact computation whenever it can:
Notes for Java programmers:
Rational numbers are represented symbolically as reduced fractions in the Wolfram Language. Java does not have a built-in rational type, instead always returning numerical approximations by default.
Notes for Python programmers:
Rational numbers are represented symbolically as reduced fractions in the Wolfram Language. Similar functionality in Python requires importing the fractions module.
Use N to get (potentially faster) numerical results:
The Wolfram Language can handle numbers of any precision:
The language automatically tracks precision of results.
Use ` to explicitly indicate the precision to assume in a number:
Notes for Java programmers:
Java code must explicitly use the BigInteger and BigDecimal types for arbitrary-precision integers and decimals.
Notes for Python programmers:
Numbers in the Wolfram Language can become arbitrarily large like Python integers. Floats in Python require importing a third-party library like mpmath.
I represents ![]() for complex numbers:
for complex numbers:
Notes for Java programmers:
Java has no internal representation for the imaginary number i. To compute with complex numbers in Java, you must import or create a package.
Notes for Python programmers:
The Wolfram Language provides a number of different stylized forms, such as ⅈ, ⅉ and 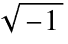 for an imaginary number, and similarly for other constants, to maximize clarity. Additionally, the Wolfram Language will automatically infer whether or not a number is real or complex upon execution. Python by default uses the symbol j to represent an imaginary number, and in general operations will not necessarily work on them.
for an imaginary number, and similarly for other constants, to maximize clarity. Additionally, the Wolfram Language will automatically infer whether or not a number is real or complex upon execution. Python by default uses the symbol j to represent an imaginary number, and in general operations will not necessarily work on them.
Matrices are lists of lists:
SparseArray gives sparse arrays.
Notes for Java programmers:
Sparse arrays are not provided by default in Java, typically requiring constructs from third-party libraries.
Notes for Python programmers:
In the Wolfram Language, it is easy to move between arrays and matrices using functions like MatrixForm. In Python, sparse arrays are not provided by default and require third-party libraries. Additionally, they are different classes, which will cause issues when moving between matrices in SciPy and arrays in NumPy.
