Wolfram言語™

ソーシャルネットワークのモデル化

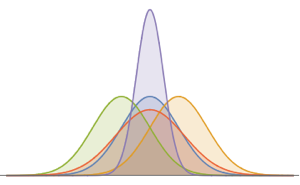
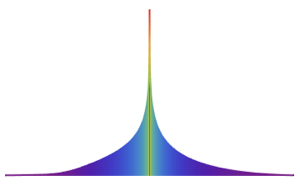
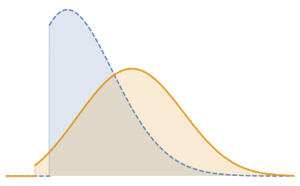
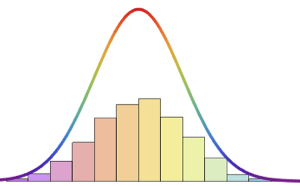
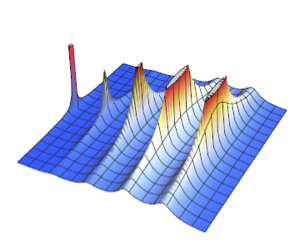
シフトされたGompertz分布は，独立指数分布と極値分布に従う確率変数の最大値の分布である．この分布は，ソーシャルネットワークにおける関心の増大と減少をモデル化するのに使うことができる．シフトされたGompertz分布のCDFは以下の形を取る．

In[1]:=

CDF[ShiftedGompertzDistribution[\[Lambda], \[Xi]], x]

Out[1]=

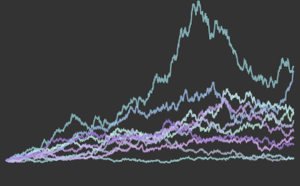
Google TrendsからFacebookに対する関心を週ごとに数える．

In[2]:=

ts = TemporalData[TimeSeries, {CompressedData[" 1:eJyFz2tPwjAUBmDA+7wRNCpeQBTRiAGvXLoNYYytPW03QHSybiYav/tX/Ume GRO/mPg0p+l72pykpbeP8VsmlUqlsT5xS/8n82smM/Nt9sdcYv4vC2gxoWlL mqYto5WVVbS2tp7N5nK5jY3N7Z2tnXx+d3dvbx/XQbFwUCgUi4eHpdLRcbl8 UjmtnJ1XqxeoVqvV65dX9cvrZvP2pnHXaLUbjWaLIJMYuk4MwzTNTue+1+1a qO9a9qA/cPq2PRg4ILnLgHPGgLkuABfSdRyHUs5AAghvyD3peb4U+IhLJoCB NxLUk0JwgXcCRNIT2AYpPS4YByo5cGBsFL+oOFaRCqP4/VWpOFQqCKbhVEXh 9BmFKopjTFEQBs9PweRxNHkYj/yh7/ueEHI8xDGAg7AAqMsodRw3OTP2HWxK XfyFbVl2z+p2kGn1jATRSZsQXW+RNkpSmxjkC/7xXxc= "], { TemporalData`DateSpecification[{2006, 8, 26, 0, 0, 0.}, { 2015, 7, 11, 0, 0, 0.}, {1, "Week"}]}, 1, {"Continuous", 1}, { "Discrete", 1}, 1, { ValueDimensions -> 1, DateFunction -> Automatic, ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1}}}, True, 314.1];

In[3]:=

DateListPlot[ts, ImageSize -> Medium, PlotTheme -> "Detailed", Filling -> Axis]

Out[3]=

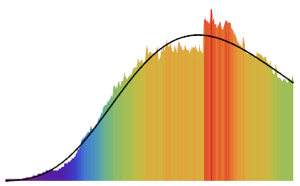
データをシフトされた切断Gompertz分布にフィットする．

In[4]:=

rawcounts = ts["Values"]; length = Length[rawcounts]; x = Range[length] - 0.5; wdata = WeightedData[x, rawcounts];

In[5]:=

edist = EstimatedDistribution[wdata, TruncatedDistribution[{0, length}, ShiftedGompertzDistribution[\[Lambda], \[Xi]]], {{\[Lambda], 1}, {\[Xi], 6}}]

Out[5]=

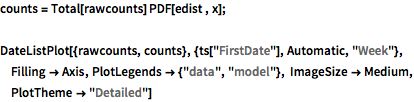
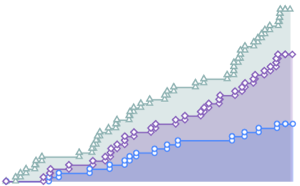
モデルからの予測をデータと比べる．

In[6]:=

counts = Total[rawcounts] PDF[edist , x]; DateListPlot[{rawcounts, counts}, {ts["FirstDate"], Automatic, "Week"}, Filling -> Axis, PlotLegends -> {"data", "model"}, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[6]=