Un cable submarino
Calcule la longitud geodésica de un cable de comunicación submarina en el Océano Pacífico.
Este objeto de GeoPosition contiene 9 puntos de descanso para el Southern Cross Cable.

landings =
GeoPosition[{{-33.913939, 151.196199}, {-33.761205,
151.273933}, {-18.12381, 178.437397}, {21.354003, 201.869442}, {
45.824792, 236.188811}, {35.366692, 239.152774}, {20.023145,
204.177937}, {-36.787961, 174.767867}, {-36.78884, 174.623336}}];Represente el cable como un objeto de GeoPath que une puntos de descanso consecutivos con segmentos geodésicos. El cable físico real no sigue geodésicas exactas, por lo tanto esto es una aproximación de minimización. Este cable posee topología cerrada.
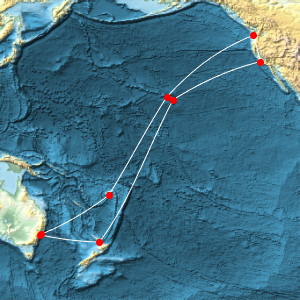
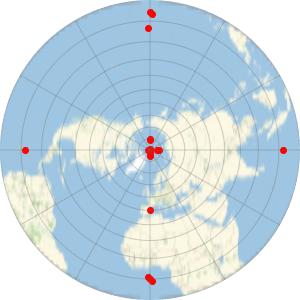
cable = GeoPath[landings, CurveClosed -> True];Trace el cable y sus puntos de descanso sobre un mapa de relieve equirectangular del Océano Pacífico.

GeoGraphics[{White, cable, Red, PointSize[Large], Point[landings]},
GeoRange -> Entity["Ocean", "PacificOcean"],
GeoBackground -> "ReliefMap"]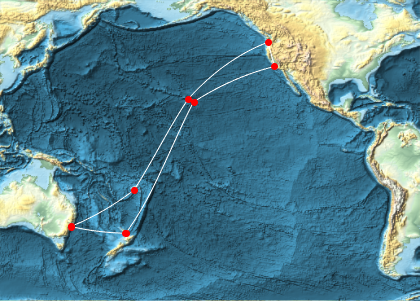
Calcule la longitud total de la aproximación geodésica al cable.
GeoLength[cable, UnitSystem -> "Metric"]El artículo de Wikipedia cita 28.900 km de cable submarino y 1.600 km de cable terrestre, por un total de 30.500 km. Por lo tanto, el cable es aproximadamente 4.000 km más largo que la curva mínima que une los puntos de descanso con las geodésicas.
GeoLength[cable, UnitSystem -> "Metric"];
Quantity[30500, "Kilometers"] - %