Un câble sous-marin

Calculez la longueur géodésique d'un câble de communication sous-marin dans l'océan Pacifique.

Cet objet GeoPosition contient 9 points d'atterrissage pour le Southern Cross Cable.

In[1]:=

landings = GeoPosition[{{-33.913939, 151.196199}, {-33.761205, 151.273933}, {-18.12381, 178.437397}, {21.354003, 201.869442}, { 45.824792, 236.188811}, {35.366692, 239.152774}, {20.023145, 204.177937}, {-36.787961, 174.767867}, {-36.78884, 174.623336}}];

Représentez le câble comme un objet GeoPath en reliant les points d'atterrissage consécutifs par des segments géodésiques. Le câble physique réel ne suit pas des géodésiques exactes, il s'agit donc d'une approximation minimale. Ce câble a une topologie fermée.

In[2]:=

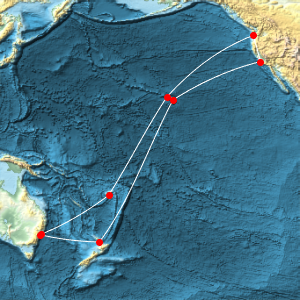
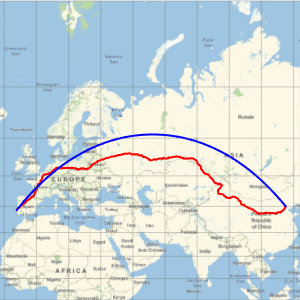
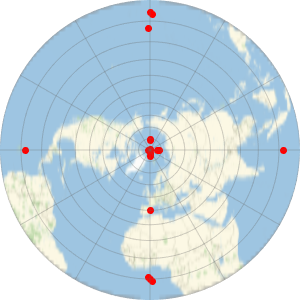
cable = GeoPath[landings, CurveClosed -> True];

Dessinez le câble et ses points d'atterrissage sur une carte équirectangulaire en relief de l'océan Pacifique.

In[3]:=

GeoGraphics[{White, cable, Red, PointSize[Large], Point[landings]}, GeoRange -> Entity["Ocean", "PacificOcean"], GeoBackground -> "ReliefMap"]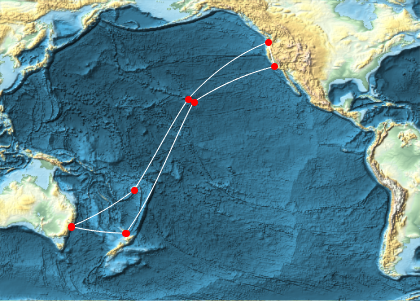

Out[3]=

Calculez la longueur totale de l'approximation géodésique du câble.

In[4]:=

GeoLength[cable, UnitSystem -> "Metric"]

Out[4]=

L'article de Wikipédia mentionne 28 900 km de câble sous-marin et 1 600 km de câble terrestre, soit un total de 30 500 km. Le câble est donc plus long d'environ 4 000 km que la courbe minimale reliant les points d'atterrissage par des géodésiques.

In[5]:=

GeoLength[cable, UnitSystem -> "Metric"]; Quantity[30500, "Kilometers"] - %

Out[5]=