생체 구조를 동상으로 변환: Wolfram Language 11의 신기능

생체 구조를 동상으로 변환

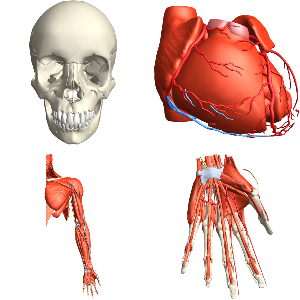
인간 생체 구조의 고해상도 3D 모델에 Wolfram 언어의 강력한 그래픽과 공간 처리 기능을 더하여 프로그램적으로 인체를 모델을 기반으로 하는 현대적 조각으로의 구축이 가능합니다.

다음 Antony Gormley의 몇몇 작품을 감상해 봅니다. (http://www.antonygormley.com/sculpture/chronology).

전체 Wolfram 언어 입력 표시하기

In[1]:=

WikipediaData["Antony Gormley", "ImageList"] // 
 Select[#, 
   Length[Union[#]]/Length[#] &[ImageData[#][[1, 1]]] > 0.8 &] &

Out[1]=

인체를 충실히 표현한 작품을 로드합니다.

In[2]:=

human = AnatomyData[Entity["AnatomicalStructure", "Skin"], 
  "MeshRegion"]

Out[2]=

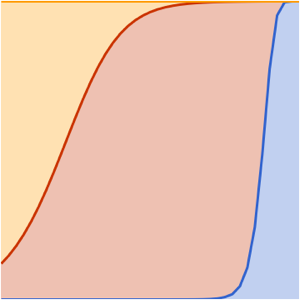
다양한 영역 함수를 사용하여 다양한 종류의 동상을 쉽게 만들 수 있습니다.

전체 Wolfram 언어 입력 표시하기

In[3]:=

pts = MeshCoordinates[human];
nf = Nearest[pts];
color := Directive[GrayLevel[RandomReal[{0.5, 0.7}]], 
  Specularity[RandomColor[], RandomInteger[{10, 20}]]]

In[4]:=

With[{dode = N[PolyhedronData["Dodecahedron"][[1]]]},
 ballToDodecahedron[Ball[p_, r_]] := 
  Translate[
   Scale[Rotate[dode, RandomReal[{-Pi, Pi}], 
     RandomReal[{-1, 1}, 3], {0, 0, 0}], r], p]]

In[5]:=

GraphicsGrid[
  Partition[#, 
     4] &@{Graphics3D[{EdgeForm[], color, 
      Table[BoundingRegion[
        nf[RandomChoice[pts], RandomInteger[{100, 1000}]], 
        "MinCuboid"], {200}]}],
    Graphics3D[{EdgeForm[], color, 
      Table[BoundingRegion[
        nf[RandomChoice[pts], RandomInteger[{100, 1000}]], 
        "FastOrientedCuboid"], {250}]}],
    Graphics3D[{color, EdgeForm[], 
      Table[Show[
          BoundingRegion[
           RandomChoice[
            nf[RandomChoice[pts], RandomInteger[{100, 2000}]],
            RandomInteger[{4, 12}]], "MinConvexPolyhedron"]][[
         1]] /. _Directive :> {}, {600}]}],
    Graphics3D[{color, EdgeForm[], 
      Table[ballToDodecahedron@
        BoundingRegion[
         RandomChoice[nf[RandomChoice[pts], RandomInteger[{100, 600}]],
          RandomInteger[{4, 12}]], "FastBall"], {300}]}],
    Graphics3D[{color, 
      Table[BoundingRegion[
        RandomChoice[
         nf[RandomChoice[pts], RandomInteger[{100, 600}]],
         RandomInteger[{4, 12}]], "FastBall"], {500}]}],
    Graphics3D[{color, 
      Table[
       BoundingRegion[
        RandomChoice[nf[RandomChoice[pts], RandomInteger[{100, 2000}]],
         RandomInteger[{4, 12}]], "FastEllipsoid"], {350}]}],
    Graphics3D[{color, EdgeForm[], 
      Table[Cylinder[{#, nf[#, RandomInteger[{2000, 5000}]][[-1]]} &[
         RandomChoice[pts]],
        RandomReal[{5, 25}]], {600}]}],
    Module[{pts2 = RandomSample[pts, 6000], nf2},
     nf2 = Nearest[pts];
     Graphics3D[{color, EdgeForm[], CapForm["Round"],
       Cylinder[{#, nf2[#, 100][[-1]]}, 6] & /@ 
        RandomSample[pts2]}]]}, Spacings -> {-150, Automatic}, 
  ImageSize -> Full
  ] // Rasterize[#, "Image", ImageSize -> {400, 400}] &

Out[5]=

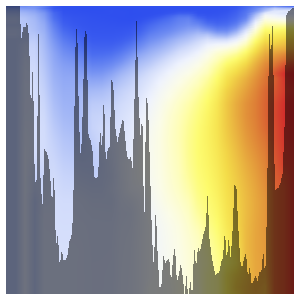
회전과 함께 다리와 팔 부분을 잡아 늘이는 변환을 적용하여 천사와 같은 형태의 동상을 만들어 더 고전적인 외관의 작품도 생성할 수 있습니다.

전체 Wolfram 언어 입력 표시하기

In[6]:=

nonlinearTransform3D[expr_, g_] :=
 
 Module[{gD, inv, newNormal, newVertices, newNormals}, 
  gD[x_, y_, z_] = 
   Compile[{x, y, z}, Evaluate[D[g[{x, y, z}], {{x, y, z}}]]];
  inv[m_] := 
   With[{im = Inverse[m]}, 
    If[Head[im] === Inverse, m, PseudoInverse[m]]];
  newNormal[{vertex_, normal_}] := 
   Quiet[With[{m = inv[Transpose[gD[vertex]]]}, 
     If[Sign[Det[m]] == -1, -1, 1] m.normal]]; 
  expr /. {GraphicsComplex[vertices_, body_, a___, 
      VertexNormals -> normals_, 
      b___] :> (newVertices = g /@ vertices; 
      newNormals = newNormal /@ Transpose[{vertices, normals}]; 
      GraphicsComplex[newVertices, body, a, 
       VertexNormals -> newNormals, b])}]

In[7]:=

doubleTwist[{x_, y_, z_}] :=
 
 With[{h = 1000, w = 180, H = 1300, \[Xi] = 600, \[Kappa] = 150},
  With[{\[CurlyPhi] = 
     6 Pi If[z > h || (z > \[Xi] && Sqrt[x^2] > w), 0, 
       Cos[Pi/2 (h - z)/h]],
    \[CurlyTheta] = -1.6 Pi If[(z > \[Xi] && Sqrt[x^2] < w) || 
        z < \[Xi], 0, Cos[Pi/2 (w - x)/w]],
    f = Piecewise[{{1, z > h}, {1 + (h - z)/h, z < h}}],
    g = If[(z > \[Xi] && Sqrt[x^2] < w) || z < \[Xi], 1, 
      1 + (Sqrt[x^2] - w)/\[Kappa]]}, {{g, 0, 0}, {0, 
       Cos[\[CurlyTheta]], 
       Sin[\[CurlyTheta]]}, {0, -Sin[\[CurlyTheta]], 
       Cos[\[CurlyTheta]]}}.({{f Cos[\[CurlyPhi]], f Sin[\[CurlyPhi]],
           0}, {-f Sin[\[CurlyPhi]], f Cos[\[CurlyPhi]], 0}, {0, 0, 
          1}}.{x, y, z} - {0, 0, H}) + {0, 0, H}]]

In[8]:=

smoothHuman = Entity["AnatomicalStructure", "Skin"]["Graphics3D"];

In[9]:=

Show[nonlinearTransform3D[smoothHuman, doubleTwist], 
 ViewPoint -> {-1, -2, 0}, Method -> {"ShrinkWrap" -> True}]

Out[9]=

Wolfram 언어™

생체 구조를 동상으로 변환

관련 예제