Aprenda a clasificar puntos a partir de distintos agrupamientos
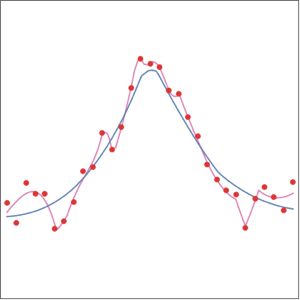
Utilice una red para aprender a distinguir puntos desde tres agrupamientos concéntricos.
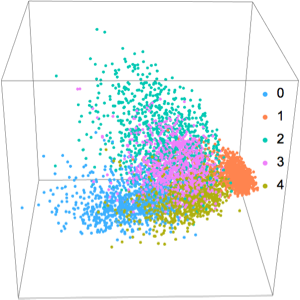
Cree un conjunto de datos artificial a partir de tres agrupamientos concéntricos.

sampledata[sd_] :=
RandomVariate[MultinormalDistribution[{0, 0}, sd*IdentityMatrix[2]],
500];
clusters = Map[sampledata, {3, 1.5, 0.2}];
ListPlot[clusters,
PlotStyle ->
Map[Directive[#, PointSize[0.015]] &, {RGBColor[
1, 0.21, 0.35000000000000003`], RGBColor[0.3, 0.78, 0.38],
RGBColor[0.46, 0.5700000000000001, 1]}], Axes -> None,
AspectRatio -> 1]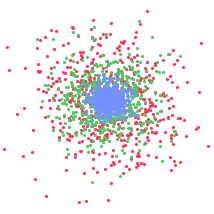
Cree los datos de entrenamiento asociando cada punto con una etiqueta.

trainingData =
Join[Thread[clusters[[1]] -> Red], Thread[clusters[[2]] -> Green],
Thread[clusters[[3]] -> Blue]];
RandomSample[trainingData, 8]Cree una red para calcular la probabilidad de un punto situado en cada agrupamiento.
net = NetChain[{30, Tanh, 20, Tanh, 3, SoftmaxLayer[]},
"Input" -> {2},
"Output" -> NetDecoder[{"Class", {Red, Green, Blue}}]]
Entrene la red con los datos.
trained = NetTrain[net, trainingData]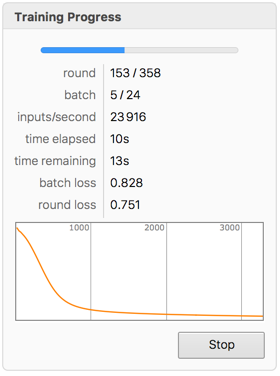
\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJzs3ftXFHmeN3jO7v6wP+6/sLP9zEx1d9XZc3bPMzNdVVPu7tOXp7vLqqmd
nu7COttPlcCz0wVYXYJaAuUFS6RGwS5BBUtFFAW8oHIRLZW7F9RESSAVSG5N
UgYmmJI+hCsz89mIzLhmROQ1wsyEN+e8uqoz4/KNyCy+b763+J8/WfdBxn+X
kpKy/n/k/ueDjzf+H59//vEX//f/xP2f32Sv/+f/mp2e9p+zc9L/a/rnf/vJ
f8+96OG2/V85/wP374Qf/OAHP/jBD37wgx/84Ac/+MEPfvCDH/zgBz/4wQ9+
8IMf/OAHP/jBD37wgx/8rICff/3Xf6WnT5/S9PQ0OZ1OevToEQAAAEBU+CzB
Zwo+W/AZw+yff/u3fyO3200jIyNxv1YAAABYfviMwWcNPnPE+jM3N0ezs7Oq
tpaxsTFyuVzEMIzvPPw2AAAAAJHgMwSfJfhMwWcLMWfwmYPPHvw20f7w+4tt
Lvw/Hz9+HPfrBQAAgOWHzxjKzMFnkGh++PYbsd2F/+eTJ0/ifm0AAACwfPFZ
Q5k9oulL4tt1xAyE7AIAAACvAp85xHYY/t8j+eHHAIv7os8IAAAAXiU+e4ht
KEtLS2HnF34ekzhWN97XAAAAACuPOKaX7w8K94efi83vw48Jjnf5AQAAYOXh
MwifRaampujf//3fw8ov4tgZfl5TvMsPAAAAKw+fQfgsMjo6GvbaduIcbKzv
AgAAAPEgziPihTsGRtw+3mUHAACAlUvMIy9fvkR+AQAAgKSA/AIAAADJBvkF
AAAAkg3yCwAAACQb5BcAAABINsgvAAAAkGyQXwAAACDZIL9EjhnvpaNFX9D6
9etp6+466p9J7OMCAAAsNwmXX5hxunL2LJ2N1IV2mnol94yhc+v/L/r5z38u
+XB3RwIf10LMcIjP6gK1tHWRfXwm/mUFAIBlJeHyy5+v0RpFHR6+j+j61Pwr
uGdjVLbmp6pz//TzeppJ2ONaKILPKvWLo9TPJECZAQBgWUi4/PJ9B2X9/GeR
55efpb+i/DJH9899qTr37mZz7odVx02Uz+pnqaU0FO8yAwDAspCI+SU9mvYX
Lr90vqL84jMzRVNT4zRl9hgVq45r0WcVadb85Jue+JcbAACSXsLlF84MX4fP
zHD/5DE0M9qk6qf4WWo5OfjXpW347Rlh/zFqO1tLtfz4i9paOtM2wL02yb12
mIq2baNtmzfTgZYB9TmZcepqOUV7tn1B6zMzfeNnN2/eRgePX6Q7ju815Zvq
u061tf4xHvw/b4zMBrxXK7x3wTcGlxm5Qcf37eSOm0mZ/PG3lVDzndFXdlz5
OofpSu0B3z3Ytq2I9uw7yN2f+7737G3nhePz966dxsP5rALyC/+5yPsxNNLX
THkfBOSbn+WTjTG+pin7dTqyZydXPu6zKjqqHcPMXQP/WW7jPiPfNa/fTEVF
e+jw2e9oJFjmi+rao/gucRw3m+lg0Re+8mUK36U9B+uoV/F5ajFk7zpP+4q2
+b5/Pr79TlBbkM+UGe+nC8e/Ee6Hf7/N3P2ovtAe/H4AACS5RMwvGoH15NpK
47G6mjEZH1HaGnUd+qGiDeBh27f0QYg2g62n7qnO0V32T6r3/6Vt0vC9T7l6
zuj4fzzc80qOy/ve3mDYrvXpvhO0SzX2JsyxRGF8LvMPG9TlVLSTBV7TP2Sm
BZRNXY5R7rMKOt6GO/apO38279oj/C7NMUN0dPN7Qb9LO8/e1d7H8Q7aHjD2
KVDq1gZNprx1fEuI9q6PuPsxEfffMQAAVkjK/JIaJL8ot/0geB/G9wOnw+73
OHxTrhdvHfxn1Xt/6powfC9YOXin+r63/Lhz49ci65MLty8urM9lkirS/pPq
+N8KGSPkNSnGNI227w27/KoME8u1R/Bdmpsb1oy/NrLl/KDi/oS/38eHb0v7
TYR7P36WRTdmXmG/KgDAK7Ks84umbvzAX+cc8Nc57Xt+q/ldf/zCFbpwfLem
zlPOZY44Z3AyN2+mrMC+lJ+rx4NYddzuff9Ft57evG2zfntGDPllPHCbmR71
56HIJEbXxPuAvyapHP20Xecz/WLfUTpY9LnmdWU/VkzXHsF36eHFL7XlO3jC
1ydVkvl+wDnkPrTv71dpzn/gQjv19d2kc/v+qL6u98XrmqG6gLn2a7cepbY7
fXSz7QzlBHwf/qULbTAAsPyshPzys9TtdN0u/g5niBG2vXv2T76xEEVFRdw/
y+iGos6eH6gJOIZcN0eUM7hMdNkhjnuYpLqA/oWo80u4x53tpZyA+/EPn1fR
sHi/mH4qy/xPAceOMr+srQqY7z1G54p+Z3hsvfzyxeF2mhLqdobxj2nStjV8
QKf65DaW0bb9muP42p9ivfawv0tjVKFqQ/mAqu+ox01dKlJn5f1d/vLPDpxU
9a/97JN61X7fHfmG9uzbR/v27aFvqtuF+ztD5wI+72MOxXfX0Up7ivZw++zj
/rmP+55ox3ABACS75Z9fPqDzjvDaz2emxmnE4SC73U59XadUbTDKsR2R5Iw/
Vj9QneP7W+Xq+tDq404FzOfi6ufL4+r7MT9qPEYlks+Fv9ebi8Q8+Llu+8b7
Wxul/Bh4Te9vbdU9T2Abyoc7rwZsw1DdenV9/hU/9zzWaw/3uxR4Hj6/tHVR
W1ubX1cX1QXkOLHdRtP+wmestBzad6SWrnTdp3HdNXO07S/8OT8vKqPaC1eo
zzEe998rAABWW+75Jei2nPE7zVS0fq2mDgmkPE4kOWP/zYDxpBOt6lxk9XHD
GvscsHZe1PklBL7vSJEfgl2vUjjbBW7jG1cb67WH+12KZR45Y6O8EPt+sCaL
vjl7S8p9vPt160Kc4wP69IsK1Rw2AIDlZNnnlyBzlQYu7gi7vok2Z2jq2iDX
Yslxdfp4dOvwD6zNL75+F4e6Lo02v2iy25x2LNMnuvklwmsP97sURX55TzGe
atbRqunn0vP+1gZF/xxD3x38LIxzfUBn+rT3CwAg2S37/GK0rd7YiLQ8Oni8
ls5eaKErF/60bPKLug8ln3oD+yQC698Y8gs/nnizwraifXS+7b6q7SDsazLY
bsuZQc02gX1Mf6y+F/u1R9D+oj5PDjXfuUM3b9401DcSOCZlhuw3L/vW88lM
+wf9LKKzxvTMeD9dOVtNRZs/NZxP/yHWDASAZWil5pfZgdOq3/c//bRGNfZU
b/xuUuaXwPk/nD8cUNdn3+37WFNPmjN+N7hw88vdo/9vwGdRrp7nNK/tg/lT
13Ts1x7u904zxyqHbjCB92+GHA6HRFpfmZmikZERzjiNj09J2zMzU2TvOqUp
vzjud2p8xLff+LhyrWaGpkbsdG7PH9T3K9h6SQAASQr5RdjuH/LoujBPY9x+
XbOeWNLmF86lbas1f5OnflFBLS0XqGT9h7p/55s2fzqIcPPL/GiTpm0h9Ysa
snP1/dRIr+4cInGcbkzXHvb3jqGLAfOBfvppOfWOC/1lUzYqCVgDZ0uz0/de
4Bp+n3xzVdFWNUQlAfOazvN9cFMd6rHR/PUq5hg9vPS16pjKMdMAAMvFSs0v
en+bB5PM+WU2cA3cUExdv85YuPlFLx8E8+E3irElsVx7BNc3e/+k7vE+WLNG
5xw5Uj/WRPvXOvt9RJmatYiV++mvebcmLVOzPjAvcK4aAMBykCz5xWjOjsaU
dttxg227g6yfppdfxOPEmjOMymfVcXn82vtG1/YP67dTzprYx79Y1f7iw6/V
EtCGoeennyrWd4n12iP4LvHunw1vPPhXqueKD9PRwPYjA/sV92eiy/iaAu9H
JJ8JAECySIr8MtOjGmurP49Ef1v+97dxmwBD7ce/0vx9/rO1pXTHcYO2f6A8
To10nLsn1PM+lPNhgr3nE1Dn//TzemnMiFXHlUzZqPbgTt8zKn3PPty8i6ov
8PNyZ+hEpmI9EZ1xoroCzxn0XmuFvCaNSbp00OiZPx9p5hjHfO0RfZf8Jm6e
VuchhbWby+i6Xe8aJ+m7I18ZPtvJt5/ec0Ttl2lXZqr+/fggnb6p7Y5oPBIA
QDJJivxiuRn/OMipEXKMLL+1v0ZvXqYLFy5QS0sLXbnSpmmf0M7Bkde3T0gM
93mNOLjPivu87H3U5xgxzC3xunZ+fK2DXwexr4/sdgeNS89HD4bx7WcX9usL
cz9+rO+Iw052fh8O/x3GeBcAWO6QX5a/S9v+z4A+hRK6fMfuy2z2m+e1Y5U/
jKwdJZGt5GsHAFjOkF+Wvz93l+v3MRg4HLIfJ3ms5GsHAFjOkF9WhvDGln5E
B64MxL2suHYAAAgF+WXlYMb7qeX4Adq8PpPS0tIok/vnmg/WcP/cTocvtBs8
K3B5WMnXDgCwHCG/AAAAQLJBfgEAAIBkg/wCAAAAyQb5BQAAAJIN8gsAAAAk
G+QXAAAASDbILwAAAJBskF8AAAAg2SC/AAAAQLKJNr9MTEwAAAAAxAXyCwAA
ACSbaPMLvz0AAABAPCC/AAAAQLJBfgEAAIBkg/wCAAAAyQb5BQAAAJIN8gsA
AAAkG+QXAAAASDbILwAAAJBskF8AAAAg2SC/AAAAQLJBfgEAAIBkg/wCAAAA
yQb5BQAAAJIN8gsAAAAkG+QXAAAASDbILwAAAJBskF8AAAAg2SC/AAAAQLJB
fgEAAIBkg/wCAAAAyQb5BQAAAJIN8gsAAAAkG+QXAAAASDbILwAAAJBskF8A
AAAg2SC/AAAAQLJBfgEAAIBkg/wCAAAAyQb5BQAAAJIN8gsAAAAkG+QXAAAA
SDbILwAAAJBskF8AAAAg2SC/AAAAQLJBfgEAAIBkg/wCAAAAyQb55dVZfPGS
Tt6ap4+r/kzv/MsY/e9fjfr8bztGAOLmzp07APCK9Pb2+ty9e5cGBgZoenqa
Xrx4Eff6KRkhv7wa3z9lac23f6b/uIehvyv/b/STgy/pzYp/BYi7x48fA8Ar
NjMzQ5OTk+RwOMhut9Pz58/jXk8lG+QX6/HtLnx2+ZtSd9zrKoBA8f49DrDS
DQ8P+zIM2mEig/xivVO35n3tLvGupwD0xPt3NwA89rXDuFyuuNdXyQT5xXr8
eBe+zyje9RSAnnj/3gaAx76+JH48TLzrq2SC/GK9v9vlpDcPLsW9ngLQE+/f
2wDwmL7//nvf+N5411fJBPnFesgvkMji/XsbAPzjefk5SfGur5IJ8ov10H8E
iSzev7cBAP1H0UB+sd5JjN+FBBbv39sA4B+/y68FE+/6Kpkgv1jvv7H/H6Vi
/jQkqHj/3gZY6fj50/39/Zg/HSHkl1cjcP06jIeBRBHv390AKxE/Xhfr18UG
+eXV4dexq7k5T//PkSl6G88PgAQR7/XUAVYS5fMD+NyC5wdED/kFAAAAkg3y
CwAAACQb5BcAAABINsgvAAAAkGyQXwAAACDZIL8AAABAskF+AQAAgGSD/AIA
AADJBvkFAAAAkg3yCwAAACQb5BcAAABINsgvAAAAkGyQXwAAACDZIL8AAABA
skF+AQAAgGSD/AIAAADJBvkFAAAAkg3yCwAAACQb5BcAAABINsgvAAAAkGyQ
XwAAACDZIL8AAABAskF+ATDfwMCAT7zLAQCwXCG/AJgP+QUAwFrILwDmQ34B
ALAW8guA+ZBfAACshfwCYD7kFwAAayG/AJgP+QUAwFrILwDmQ34BALAW8guA
iCXGNUkutyfmYyG/AABYC/kFQOC5T7kZGZSedYrcMR7LzPzi6G6k2tpaaux2
6ry/SH2Xz9K5c+eCuzxAiwbHd9lbqWRLFqWuXk2rOalp62hP9RUaX4i+zE8H
aigtNZWydrbQQhjbR16G2K97YeIe1ZV8yZXzXd85V3Pl3Vi0n67bZ+L/XQSA
kJBfAATP79MOPr/knSFPjMcyJb8sjNDh7DcpJSXF77W9xGi2m6MD76TI2xj6
Wmffx1SX/ZMg+7xBlbejq8t7dv2N/xi/Ox0iv0Rbhliue5F6Dn8adL/Xsupp
Pt7fRwAICvkFQJBA+WWyu4pWBdarvz6grVO9dynd9/5HVFZ7ztdOo1VNtY19
mnaI3tJfSMdeu7OO7BMump9naKDtFK2RzruKWifYCMs/Trt+7N8/t3Es6LZR
lyGG6568kied84dr91KXY5LmFxaImein41t+K7335s6O+H8nAcAQ8guAICHy
yyK1K+r0lHeLqamuwP/vb+nll5v+ev7XR8Lqp5H3uyvlg4LWKe377ANaJ7z/
kz13IrqGpckL9IbQdnLRtWRNGaK9bkW7zV9vaNHtWxo4/gfh/mfQvYUg5QeA
uEJ+AWNecjMucnv8f/t6mFHqt/VSb28vDU0+02zvZSaov9f/vq2/n5yTjPGx
WS8xLobcXuO/7VmPm1yMm7xByvTS6ybnkM1/Tls/Dbvcoa+L22e4X9inf4gr
p7APl18K4p5fHkv1a2ZZh69uZgf+ZJhflmav0Xv8e2/r9S0Z8w5USHX00KL+
Ns66fxb6gE5E1JfibFgv9HcV07RFZYj2uuV2m1XUapStpFz1PnXNI78AJCrk
FzDyzHGKMrj6PK+mkzprtvn+XZRWcV/elp2m5vLNqvdF6XmH6AHzQntse7Xv
/cyjRnW8h07npvm2Od7/TFOmzXX3aaznuO45c0qaDes0fp9snX2ySq6Q5/lg
ArS/zFHDxg101v5Ueu1pn3F+edr7jdCW8J3hOFWj84za7WR3GI9vEXOIUTuF
vgWqSxP7X25YVoaor5sdpE1CfrnOGGQTFvkFIBkgv4ARMSvIsqm4vJIqS4vp
RI/Q3u99RPsz0qVt8kqPUVNrK9VX7lLsV0Ddrhe6x958wji/nM8X88tc0DKV
VJ2m1tYGKi/MkvNVSRexAcccad0t75e+g6pqaqimpop2ZPvLn1tY6Ms2iTD+
RSlYfvH2+dswfntokPg8cPvyWfr222qqrq6mc01t5HA9jfK847RLaAf6Zdn9
8PdjHwjtGym0+/aTGK/duAzRX/cCHVntP+ZbRv1HdWL/0WfUv4j8ApCokF/A
iDIrpOcdo0ce7e/yvqrPhW020KWhOdV7rOsefS1km/S8C6pMYEZ+Sc85RINu
dZkcTXuk8nQr/76eu+WbG+1va2kJaJ95QpfL1yuuNXnyy0Oprn2f1qzSn0vz
dtYRGg/7fIvkclynratfk8eARNAGIeYKflxt9GNHQpchluv2PqyRtvnRh8V0
3e4kl8tFE6P3VON389t0xuQAQMJAfgEjclYooNtunbrIOyjlk4Pd+n9rv5hq
kdpJrk6+0Bw7+vyiPp5smg4J7SknbPJ+I007/ftlfWswJuMxHcsVslZO8uSX
vv2/UdXZH245TG3dt6mt6RhtWvOa/N7vjhiPE5HGhAT6jG4Z9bEY6N3/c2m8
SqTjiSMpQ6zX7X14RhhjrK+gNfi8KQCIP+QXMCJmhcC2k8D3M9IP0IThcbzU
XJgmZJwZzb7R5hfjjOGRzifvJx9rz9U/G17vTOc3SZdfekv/I4nrpBy7pc2Q
Aw35Up2c02jQnrAgzPN5/XV6/XV1Pf7u2lIaCrsd5TGVCv09H5+K8HdEhGWI
5bqXXJ20Trl2zOurKDUtjVa/82P5tR+/R1W2WdP/mwIA8yC/gJFQWUHON8Hr
e8f5rb7t1iuyinX5hTtf/VbD/FI7pJ03JXo+djHp+o9mbK1U/W01tdqN69or
W//Wv/+vj4Q1j2hxYZp6z+2W2yfeLg6r/4mfE7RKyBRnRiNdMyayMkR93dL4
Xc6PMqjRPqnaZ37iFpWm/rW07szFCa8pnyEAmA/5BYyEnV92XQmY46wm5onN
CZBfGp3Pja/Zmwjzj7SC5ZdwSPOUQ8xnDsQq+lj22UI/E2pGWhduWwTjbcwt
Q6jrdjb8cxhruzym/avDnUMFAPGC/AJGws4vIfpbguaXuocG+5mbX07na+di
B3o+cibp+o/C8vSmf62UlI/oVkTzgReludCZIfuDFqk5+wf+Ov9LM9etjaQM
oa9bHJ8Tak7V096vyXDNYwBICMgvYCRUVhDr+4z0r2nQa/y37ElhHZcjtnnt
sQ3bbp5I+5nS/iKMidl2zigvvaQxYYxv8uSXx3Q41T8Hx3AttpeKulix/8M6
/7oquWeDjVPlMsmmvxDq+xBr8LKD0lq5X3V/H9Z1RV+G6K9bHPcbKr94xXse
6fp4APDKIL+AkdBZYUJa+2XXuVHdY8z1VUvzhdoVa8CI69dlpO+lUd1zn5Xm
M8eeX17S1LVvpHVfHujMA3/JPqK9Gck2/2hOWsvkV3uM+jnmhLpePSdo4Pjv
hfYF4/p5abZTaL8IvZaL9+FRaT5zuGu+RV8GE677h9toxLBs/Bp8/8G33WuZ
kazdBwCvEvILGAknK0jzkjlljXZVW8pUb6201m1aWZd632d3fWv1+9bLLbtC
DCu/NzvUIr1nVn4Rx7b451Dvp3sueRwMyzygQ7nyGnzJNP5FWl+f7185dkM9
Z3lxnOo2yc92rrIrrnnytPT6a1lHaCQgczwd7aJ10jygz6g/xBykgcP/GNEY
4VjLEPV1O+Vzpny4l/qZgHHGi9PUUCSvAfPV9fDakgDg1UN+ASPKrOA23M5D
l0sz5XVts3MpPz+f8hV5gF9zZdSr3dd+eqt6bd/SUirMzdas7W+UX4zKpJtf
OHP9Z1XHzS0sptLiPHnt4PJy//OPgl5veKzKL9p2ijmqW/cDxXzjVbRxSykV
bclSrW/y20Pa/p+H4nOKxDVUsrdSSUkRrUt9W/H6G1z9H2oNX7k9xL8ebvjX
Fn0Zor9up+acm2jLli20ZeNa1b5vfRnpMxkA4FVCfgEjz0eE+cTbW0K0R7Bk
bzqo+1yhkvrOIFnAv1/gPtn5e6nbOUnXhTVxzw0/i6hM4nztczpzpZ8522iv
MlsJa/UeveQg9sUj33p86dv117uJhJn5RZpHs9ZoTbg5aq8u0F+P7cdr6Fj3
pOGxJ2+foXXv/Ei7H7/uStYBuucKPQ9anjedQlWOyOcbR1+G6K97xnaR1q3+
oe45ffu2GY+TAoDEgPwC5vGS2+0mj8fje7a0hw1zP5Z/pjRDDMftfjXrbXi4
crq5cvLlDXxOkhnMzC/hW6CJUf55iKPksNnIPuoKu/1g3jVBdruNbNx+NruD
XPOL4Z93YYRqy8up/NsGGjd4jrS1ZYj+uheYcXLY7eQYHSU7t+/oRJBnpgNA
QkF+ATBffPILAMDKgfwCYD7kFwAAayG/AJgP+QUAwFrILwDmQ34BALAW8guA
+ZBfAACshfwCYD7kFwAAayG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBfAACs
hfwCYD7kFwAAayG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfwCYD7k
FwAAayG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfwCYD7kFwAAayG/
AJgP+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfwCYD7kFwAAayG/AJgP+QUA
wFrILwDmQ34BALAW8guExpLb5SIX40mAskSP9bhpctJFHtb6cyG/AABYC/kF
QvLcp9yMDErPOkXueJclBvaTf6QM7jqO9M9Zfq5Y88ui6x6dqz1H584Fwb3f
72IjOu7TgRpKS02lrJ0ttBDG9s7bjbQrey2tXr3aJy17Ix1r6qP5SK9pvp8r
by3VclptM3H/LgBA8kN+gZCe36cdfH7JO0OeV3JODw31XKVrHX2m5iVH/VZf
fjmeBPnlad/XlJKSElJ+15OIjtuz62/8+/7udIj8Mk6H0/4yyLkzqMu1FOZ5
H9OR1fK+f7nzxiv4DgHAcof8AiG96vzy7K6vvScjYwPd84RbR4aWTPll4PDv
fXX9h1v207lz/naLQNXVtXQvovaXcdr1Y3+GyG0cC7LdIjVv+gspb2R+20yj
LobmmQlqr/2K3hAzzA+30chiGNdy/Peq7POrPXes/w4BwLKH/AIhver84h30
nS8jo4AeeFdmfunb/xtfXb/v3nPTyrQ0eUHIHm/QxSBtJ6yzRsoau7u+17zv
fVgjZZivQrT/sA/FY71B2RvXIr8AgGmQXyAkMb/kyPmFmRwmW28v9dpsNDQ8
Sd6Qx/GSyznk36fXRv1DTmI82rYDj9tNzNh3lC20v1x1zpKbYYhxG40d9tLk
UD93TP9x+bIYjc+V88sz3//3ul00xJXfX55hcumUJ1qx5peeol8I+SGy/qFg
nA3r/VnitWKaDrLd016h7+rXRwzHuYjlC55Fxmnr6/6c8+bOG/T04VHkFwAw
DfILhCTml+0txDAPaH9uui8HqKR/Te1O/baCsZ5aoT9Iq+TcALHits/uCrlF
T7amL2nGdpEKDLatuOTQlEPML+f6x6izapvueSoujZpyz2LLL49pv2+8yCq6
OGFWplqgujQ5SwTb9qn9DKWtXk27W437mMT2oZ8EySK9pb8Q2l6+oBHu/3v7
/oT8AgCmQX6BkIT8wtfvYr7IKtxPNTX1VFNVosoNVwMyzEzHAfn97B1UVd9E
rU31VJovZ6A9l8b927PTdLmqiipL86T3tpcfo6qqSqqsukyMol1l7Po3ivMW
UFVDEzU1nKBCRbbaXndfVRYxvyjLU8Pt19pwVJWDDvbG3uYRW36ZE8a7fkT9
i0v0dPQWnav+lr6trqbq2nPUdvth5PN/2AeULvYJ3Y71+uak8bgFrVO623iF
thZeld3/nXiK/AIAJkJ+gZAU+cXXRnFtRPU+yzygvdn+3MD3Mclzhh7ToQz/
6+uP3pXbWXxYulMjtIFkVROjfG/pkf986TtoUK8vaO6W1J6TVdKi3pc7rr1p
j5Snuhm5zUaZX7afuBHQ5/WYzhem+a8h70LM43xiyi/sIK0T6v530941mP+z
ig51T4Z9TG9fhbDfR3RvIbYxRc7mPGlMi377kNxvpMwqyC8AYCbkFwhJkV82
n7ivu83SzHdS28ylyRfC617fPOjW1h6a1ssh3HELhPYTVd+QdL4C3flHI007
hdzzrcE4jid0OtefRY7Y5qXXxfzCj0PWm5ctX0MBPYhx3lNM+eXpTXpPmVV+
lEGHzrXT7e42Ol6yQZ7/w6m0zYZ1zN79PxfmTZ8Ia90XI6zztHT+j48N6m4j
9i3x85PGFa8jvwCAmZBfICQpT2RTO2NUr3vpcnGmvz/o2nh4x/XI+eWBQX7R
5ggPnc/3Z5M9V/9sfGzWS16vV9XmI+aXokaD8innPcU1v3TSKiEjvJZ1IqB9
6aVvLbit76SoxpYEP+ZjKhW2//hU9P/tLs120hoxO3E5SK8PS5lvKu3qvkTk
FwAwE/ILhCTmiazqoPNWHOe3Cm006nqbZUapo/UcVVWWU3FxIeXn51NudrZq
/Eo0+aV26FlE1yHmF8P9gp43MjHll8Vpulx7jKprr2izi2Bp5pKUcfbZgj/X
YWn2mrDtG3RmNMrxwN67Up8Wn5mGdNd9Eccdp9CbX3Zo3kd+AQAzIb9ASNL6
L8HHhYj5QJlfxq4dNJxPlB1jfmkcjmxtlJDrvyRKfgnLAh1PFdbgva5do0Vp
5oo4XkXdnxO2xRFpPAu/7u6tef17I83PTvmMhnTe9w7488svy/T7IAEAIoH8
AiGJ9Xr6AZoI8uxDMR+sF/ILP55EzCs5pSfJ5nSRh+/TYVnpuNH0H50W8ou4
jku4lld+kceZ/LIsWHvGIjVn/8CwTSS0aalNhR/722XYfzhHB96Rx+WkpqVS
aqrae1IGWkWrU1fTO3+/hhpHvfH/fgNAUkJ+gZAU43cvOV8YbPdEyhXi/OOx
1t3+8bK7WvTXt4sqv3ipWZgntK3uoWGZWQ9DLhejWssuWfKL2M8SPG88lvLC
7ltB+o8Uc5m+6g7eTqM1R8fT5czRGnQtGnV+CVfQsgMABIH8AiFJOSODsnZd
0c0ic33VQlvLBmpn/BlHHA+z/qh+PS7NIwrMCx6DeUmCmU5h7Zf0HQY5Y1qa
t603/yjx84s41/l9w/YOeT60vL6K7nbSOizcsQz6ffQtUMPGv5PmSZ90hG4n
WZxniGEMzC+QU+jHeuvL74hZmOden6fFeH+3ASBpIb9ASAHrv+RVqNeSm7Gd
lcaypO9qk+b8PHOImSabzvXPKI7pJXurclxMYF6Q5z+XBaw148M+oq+FfJKR
tZfuuRT1t3earldulvLNoFe7/kui5xdlm0nKD7+grgl1dpi5fVIauxtqPvTA
4X8M+SwArUVql9bOTaF9t/2f3eLiolYE14X1dwHATMgvEJLQ/pKeu4OKpXVz
s6m4tJQK87PkHJK+lwaV9T47Qcey5fVws3PzKdc390hc/7ZAWIcusJ2Fpc7S
tYp1cnMpN+8YjSoy0/OxFtWzBnILi6m4MF81RrioUf0sgJD5JUS7TyRiHf/i
HahR9bP8fdomKikponWrf6h4PYNuGY5H4cnr5P72kP5aLXrE/ivJ68H6gMJf
Dw/zjwDATMgvEJKwLkr6dr7v6AldrtqlmU+UV36eJrx6+47SacXzAOTnApyn
adZDlwvX+p6dNBj4nGnNftpMwbru0aHCLM2xs/P30tWhGU1ZxP4sw/nT7CPa
y7fr6JUnQmaM3/WOXqOtqW/r5oYPvzxO4wvB95fnTadQVRj9P9J5FX1ToWWE
nV+8AxVhjDcGAAgP8gtEhcsebreHPG6G3GE8t5n1itu7yaOXcwzPI6xDF2Te
k9fj8T+jmuHLkhjzWcycf7TAjJPdbqfRUQfZbA5yzS+Gt+/CCNWWl1P5tw00
rrteCwBA8kJ+ATDfq5g/DQCwkiG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBf
AACshfwCYD7kFwAAayG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfwC
YD7kFwAAayG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfwCYD7kFwAA
ayG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfwCYD7kFwAAayG/AJgP
+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfwCYD7kFwAAayG/AJgP+QUAwFrI
LwDmQ34BALAW8guA+ZBfAACslVz5hSWXc5gmGU/c7xssT6yHoclJF3nY2I6D
/AIAYK1kyi9jl3dSRkYGZwPddi/F/d4lomfDLVRcWEglRzvJmwDlSTb2k3/0
fceO9M/FdByz8ovzdiPtyl5Lq1ev9knL3kjHmvpoPsR+LnsrlWzJolRhv9S0
dbSn+gqNL0R2fpf9uu844vlTU9dRWW07ucI8jqO7kWpra6mx2xl0u4WJW7R/
I3ed78jn2VleR/0uNu7fCQBITMmUXxynvxDySwZdmnwR93sXDa9rkK61XiOb
M7b60Uhf1ee++5O+/QrySxQc9Vt99+943PPLOB1O+0tKSUkxkEFdLr0M/5jq
sn8SZL83qPL2TBjnf0wNW34Z5DirqMo2a7z/wggdzn5T3v61vcQYbPuwIT/I
eVJod+tY3L8XAJB4kim/vPSMUse1a9TR40jauln8+z7z6H0Ljj9Nx7LTfcff
1z4V92tNRomRXxapedNfSPV35rfNNOpiaJ6ZoPbar+gNsW7/4TYaWVTv21v6
C2m/tTvryD7hovl5hgbaTtEaRfZonQjWrqE+/1sbjtCt0RnfcezdJyn9dfk4
13Uy1GR3Fa0KzCG/PqDbZuRsXi9v82ExdTm48zCugPOk0L5b6DMGALWkyi/L
gFg/bq4zf2zE0kwbZfvap7KpnUH/WiyfTzzzC+uskdseur7XvO99WCNlmK+6
nsjvee9KGaWgVSe/sg9onfD+T/bcMTz/04EKOTudGtTZZpr2rxGyxSf1tCC9
vkjtivyU8m4xNdUV+P/9LZ388vQmvSds+1rWecVxRI9p/2rhWL87ofM+AKxk
yZVfWHJzf5sxHq/qddbjJhfjJlb4/26Xk2y2XurttVH/kJPcBmMxA/djPdM0
1N9PQ8ND1N8/RC6Pwd+orJcY7u9ht9f4b1jx2FI7Eesht4ehzvJP/e0vZW3c
dbiJYRj9saJeNzmHbNw19HLX0k/Dk4xUTiNT177x969lVWva6tX3ZJg7d6hx
BR7p/L02/30Mb0yrlyaH+v37cecaGp4Maz8vM0H9vn246+U+Ayd3vaHubaSf
t+p+TA5L1zY0zO3j9b+eCPnlae/XQpvFEcNxLj1F/pzwK0UO8Uq5I4OGFvX3
c9b9s5QHjI7dt//nIc+/NHtNyB5v0BmpLecxHXhHyD1lHb68wQ78yTC/OBuE
sqR8QSNG3wvpmj6j/kVkcgCQJVV+8dynXH5sR9Yp8kive+h0bhpX5xTQPdcw
nSzMlMbIyDZQY39gX7243wZ64PXSnZoinf0yqKzRrinHM3u10AdkVD+Jx+br
wWe+18R+Iz3q47DU17RPf9usr6nd+czgnF66XLzWt916Rd8U67pH+/PTdI+3
/Win4j7KZmwXqUC3rNx9DDLmwXi/bKq45NDfj52m5vLNuuVLzztED5jAcU7R
ft4C7yidLNbbJ5suDc/RSNPO+OcX+xlKW7066LiPvv2/0WlHmaNRu53sDuPx
Lc4Gf3/NX29ooUXdbRaoLu0/+LbJaQzWB7lAR4S2kY+PPZLO37BxA521P5Wv
pc8ov8wp9tdr45EtLi5wXsHvFwBIKkmVX57fpx2+eu2MKr+cD6if0/P3Un1T
KzXUlAn9KX5XVWN+xf02UGlpnlTvVdQ3UWvTCdohjCPx9/Wox6o8c5zyv37C
OL+IZRLrwVnbJaqsqpTr9/QdVFVTRZWVlXRJUdc6zm+VzptTfIhar3VQa8NR
RS7YQN16fUPsI/o6I11d93oHffdLvrbL1NHRSlXS9XLZqeKu6jhj179R5aWa
+nqqr69S3Y+jvdr6UbUfly2qGpqoqeEEFebK+20PuI8vvY9of4b8fl7pMWpq
baX6yl2qY3W79D63SD9v//n2Ks9Xfoxqamqoqny7dI8K87Pinl9Ck+t+3X4i
Q+O0S2gf+WWZ0fgruQ0l+JiTRWpY9wPfdn/15XeG2xnmF6nviG+/4b/PC+S4
3Urfluykoi1FVFRSTmfb+ohBbgEAA8stv5QF/p3vGaS9Qt2bo6qr1ftlbT9D
06p+Bw91VsntAsr5TtHkF9FIgzj+5aF2P3ZUql8rNONvp+mk0Kaz/oR23+eO
s1IuGvT6881Y625//Z5TTRMBfSqzdw5LdfYDYfuXz+5KOSnv6M2AtpkndLl0
vXCOvTSqPN7cLV+7mO8+lrQE9F2xZG/aI7VxKLOXOFeKL8OlIfV94tuNxDyW
nnfBhM9bfb7GIXX7zNxIi3QNiZ5fnM150lyii0HH4YoWyeW4TltXvyb1L92b
N+qLkcfuvrnzRpBjTtOuHwtjU942nltkmF+8N4WxOhnUbb9O6xRjdQPnOYU3
XwoAVprllF+ySrp095u9cUCox0+RW2c/TX0seUKnhW2UdWEs+UUav6u3r5Rf
CuRMocDPve7p6KFB13PNe3Zhbnn69hZpzI2YXzbr5B2+v2mot4d6eh3SvRwT
+k7Sc84o7pPCkpyvDnbL40bFPpeMrG9pWvd+PJH6047Y5v2veQelfKI8ltKL
qRYp98htKVF+3or2qX3t2jGxvv2kTJe4+YV1npbG7gbtd/HepXTdPPAZ3Qox
tnvmSp6UHVp152jzc54V84YM5hbxQre/rKJVQnb50Ydb6Wx3HzkcdrpSrZhn
xTnp8AYtMwCsPMspv4hjTQI9Hzkj/B2vv19R46jhOfXqQsvyy8sJqT8lp/Q0
DTPanKLvidQ2U3RpXHp9plPs09lAdT0jIeach76PPLH9aL1Ufnm/PVf/bHx8
1kter1cacyvew4z0AzRhWCYvNRemCRlnJuxy6n3eyvPpZ1X//T+UnZ6w+WVp
tlOeAx1k/K3PgjDX6PXX6fWAto1315bS0EKQDMMOSvOUUlI+olO2Sfm9xcfU
fvjTsOZG84zyy9Peb1THyDymMx9qvp82iWUPMpYYAFam5ZVfDOqcEPvVDhnX
1+KcZGWbhHX5hcsHQpuJKDt3B5VXnaYO24g0R0ZD6r/JVo/54PtSFOM9+PcL
i8upvrWDhl1uTZlPS/0yBVReXkqlpWr8a9KYIJ38Euw+BhLvofoz0RLHA+nl
pUg+7/DOJ4+BTrj84r2ryBRfGM4vMrK4ME2953bLbRpvF9N4kO29D8+o2j9S
Xl/F5aDXFa+9T99W7/T//yjyCz9/SVojRjUHW42fS/4G2mAAQAfyS4i6ShwD
qxhXYmV+4c0OtVNlcZ4qx4hK6u5o2lHENqKMdJ3+G3aaOusrKD87XXOs9Jy9
dFvqi9KOiw1GL080DofbXqTIE7uCrxOsvV8x5pcwz5dQ+WVxhLZKbSgZdMtw
7EporCKX7LMFXxNukZ+7tvF3mj6oDzfup36uDDPNn2vmcAcKPf4lhXYHHSc8
J60Bs/u2fj8jAKxMyC/B2w3EMRh6daHuGNwQZQonv0hYD7mcQ9TRWkdfK+bx
bDun7O9iqbP0U93xqoE8bhcN2drV83ukXCa3vxzk5xcJ/T1GWFa+1tNh9DsF
kvJEToj2F7PzS9DzhZlpw2BefpmW13BL+Yi6Yl6XcJHq0sS16cL873hxgeYZ
xrdW0cKi9jjR5Rd5rb3gOUqea4X8AgBKyC983Wi8lv/UdXEOj3b8i/Hf8vJ4
lJjyiwpLd2q2aftAFHOWjgR7Hk0A1nVbmltd58sdHmmsSdBxLBryGJVthnnO
/1xnl0teq08co5KR/rXUrqX1WLqP0rjfKD9v+Xw7jM+nNwc9Subklzk6nh7u
mv8v6WGdf0xt7tlgzwuS5xf9skw/dyy6blJ1ebnvOZH6a8RwnnZKa+dW2Y3b
3YzXf1kIM0eNS21PeIYAACghv/jHe9zW+7t2aVQaT6usm8X163zzlnTO90yc
y6yXX4R5Qnr5xTvZRqXCs6P11tp9IY5LVWSp52MXpWu451Feg5c6a0qosLCU
2nWfdenV3DdpvC93XY90x7hyGaqhgkpLy1Xr6Mn77aAHHr1sME2HpIwl5hB5
rPKuc/rjp+f6qqVxO+0u7fyjyD7vCd3PUmmkabfh5xap2PPLAjVs/DtpnnQ4
Yz8Gjv9eGOtqPJ+ZHwMs5g6j9gxp/V/++Ua67T2LdGXr3/q3ea3YYM6ZcCzD
/MJ9b9o3y/O5DcYTP6z7gzTeJpZ+MwBYfpBf5LXauiflOpl1P6Jj0vsb6J5b
8btTsU5KTtkVYhR1/exQi2oN2sAyzYnZJ2s/PQqo66U2Ak5Fx4jqPdY9SIeE
PqS0ki4p34jzgdRrpPDkfMKv//JI9bwAlkauHZSywVUxGyjaH9JzDtGgW71u
XJ+0jkuGvE/AfhlZe+mecn63d5quV27WbfuQ5l1n+Nc5VrZlTfXWSmvRpZV1
qcoR3ect3yvfOKKmPsX5WHK0HpS/C3HPL+rnCO0T1j9ZXFzUUn5HJk9L+7yW
dYRGAur7p6NdinVWPqN+ozlISyO0SfEMo3su5Xdnga6U/pN0nlDr5wXLL3yu
LRXWykv54RfUNeFV3YM+xXOpg69FAwArUVLmF9X6JMrxF8b1WYHOfmI9mFuY
L9Vbufn5lJ+fr6rLDvZof0fbT29VbJNNxaWlVJibrRnnGlimFzPfqd7Pzc2l
iqtjUpkulyrWts8uoPLKSipXjeXl24q0bRHbdNowng23qM6VX7yfKivLVWN5
1x9Vj5l5NnJRtYZtfnEplRYXql7brvPsyedjLaptcguLqbhQfR+189QDrzfX
d+/zFWN9+DVlRr3qfaL7vHlP6Hxhmur+8p+bdD+4fFVemhP3/CLV+dLcH6O1
3fxjYpRtF6p1WfixttlbqaSkiNalvq14/Q2qUqzxr2c2YH7zu2mbqKhoC61R
lOW3ZaEzhTK/6LUJLc1cUj2r+t20dZSWlk1rVimu8e1izXO2AQCSMr9sV7Y1
eKlZmPN6bthg/KjufnLdz+831XFEkz34NpmrQ0b1GL+u7EHNPtn5e6nbOUnX
y9cblmmsp1adIVR9SR5fH01uYFn43FB+nh4p20QU6942OvXHIHgnb9Ohwhzt
tWXv8K0Jo9dP5XXdo0PCOvqB13bJZvz3Nr9m7qFC/f2uDhmtoeq/j9k611tS
36mzjl60n7d8f2/U7NGcK6f4mK+9aeyyv00okrngemLJL96+iiB5JZC272Xy
9hla986PdLd/N+tAQHuKsaeOS9xx9M75Bu1pDO/apOcvrjV+fjQ/3mZX2lu6
5d1QdgXrvgCArqTKL6bSWQeN9ZLHzT8T2qV6vnFQ3D5uYW6G2x3Z+hS+uTys
UV3CCmVhgjyjeoJa+ecTNVwPePaBFuv1SOVk3OGNg/R65PO7PeFfm9cjnyv8
/bj7yF2vh9uXcRlcr5n454Hz5+O4Qz6LO3LWPv8oPPOuCbLbbWSzcewOcs0v
Rn0cB7f/qMNGt20Oy55JtMCMc+XlzjPq4P45SsxC/O4dACQ+5JfY+woAAiVC
fgEAWM6QX5BfwHzILwAA1lrJ+eV0buTrrgGEA/kFAMBaKze/8Guq8eM7whzn
AhAB5BcAAGut5PwCYBXkFwAAayG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBf
AACshfwCYD7kFwAAayG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfwC
YD7kFwAAayG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfwCYD7kFwAA
ayG/AJgP+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfwCYD7kFwAAayG/AJgP
+QUAwFrILwDmQ34BALAW8guA+ZBfAACshfyixJLLOUyTjCcBymI91uOmyUkX
edj4lyUxsMS4Jsnljv3zR34BALAW8ots7PJOysjI4Gyg2+6luJfHavaTf/Rd
75H+ubiXJSF47lMudz/Ss06RO8ZjmZlfHN2NVFtbS43dzqDbTd4+QxvTPqTV
q1f7fbiJToXYBwAgWa20/OJ1DdK11mtkc2rrbMfpL4T8kkGXJl/EvaxWc9Rv
9V3rceQXv+f3aQefX/LOkCfGY5mSXxZG6HD2m5SSkuL32l5idLddoCu7/rO8
XYC3vmyhhXjfWwAAk620/CK2OWQeva993zNKHdeuUUePg7wJUFarIb8ESKD8
MtldRasCs8ivD9C8zrY9pb+QtvndzvM0yszTwvw4NZd8LL3+5s6O+N9fAAAT
rbT8ItbZm+swNgH5JUBC5JdFalfkkZR3i6mprsD/729p88vSzAV6Q9j2t4fu
aMtx/A/Ssc5MsPG/xwAAJlkx+YX1kNvDUGf5p/72l7I2YjxuYhhGMX6VJTfj
4l73Buzv9b3u9vh//7NuF/Xbeqm3t5f6h13EqrZliXEOko17z2az0ZBzNmTZ
PMyob/te3z795HTFMn7UQ84hm+9Yvdz5+4echuNzQ+UXL3edQ/02uVyTTMC1
yvixwC7GLb3Peqa5fftpaHiI+vuHyOUJXXe6XU7uPPx94Ms9zH0OofeJ6t55
3TQsXhdXNuek2/86l18K4p5fHtOBd/x5I7Osw9fvww78yTC/9B3+R/97bxv1
Lc3RkdX+4/2yTJtvRMzEEHV3t1FbWzfdttnJNb8Y0/UDAFhtpeQXsd9IT+ZR
oZ5RjN9U1l/PHKf8bTb1d8neuk97jKy99MCzRC+Ze7Q3N13zftau0zStlyHY
aWou36xbppyyZv19gpixXfTVv9rjbaBGmzZHGeYXzyidLl2vW670nL10jwkc
G+Sh07lpvvM88HrpTk2R7r5ljXbdcrOue7Q/P013n+1HO/WzRJT3bqznOGXr
7JNVcoU8zwcToP1ljho2bqCz9qfSa0/7jPLLNJUKWefTs2PG34srecL4mWIa
D7z3E5206T39cTO/29mi218FAJAIVkp+mbVdosqqSrl+T99BVTVVVFlZSZf6
hbrdoP9AzC+yAqppaKL6yu1yvZ67g3Zk+7NLTvEhamptosriHDkjld1Ul4kd
pf3ZctbZXnmS6uvrqapcccycUzQd5vWNXf9Gkae+phruWPX1VVKZeEd7Z1T7
6OYXdoIOKctVfoy7llaqryqRj5++l0ZV+cBD5/P9+aW0NE/KTBX1TdTadEJV
hs11AeOOvP7MIO9zmTo6WqlKOg537yrumnLvRlp3K66B//xrqKZGvke5hYW+
bJMI41+UDPPL05v0ni9rrKKLQfqGlmavCWNp3qeuecW8Ou9dWiPllVX0ZXkd
NTWdol3Zv5YyzF99iXEzAJCYVkp+EY00iONfHmrfDyO/8O8p/7afG7qoyjYV
Heq/gx1NO6X60tdGI7xur/lCer3d+Uy1z9xQi68diH+/6NJ46Ot6dlfKZXlH
bwbUvU/ostiWEpA79PLL7I0DUkbrdqnbWVjXbek8R3ufKN4T84vQlrH9TED7
h4c6q+S2EuXcrjEhU6TnVNNEQJvJ7J3DUq554I3x3s3dkl7PKmkJ6Gvh7lH5
etVnnBT5xXtTyB/v0635IPP9vWLOUW/3sE4YG/N2MY0sqveZaS+Ucs2theW/
lgAAJJ+Vll+k8bsndOqWkPmFq9MZ7e/yG0Ldl77rinZ8CPuIvs5I9+17T8wv
0mvGY0+mrgttBVnVIdtgxoSMlJ5zRn/dkqVR2iuc72D3E829UJbBP7+8ldr7
Z3TPJWYH9f1T5BdN24zoCZ0WtslRtKeI+WXzCZ08+dJLQ7091NPrkD+PKO/d
iJgjs741uJ+P6ZjQ98ffx+TKL59R/2KwjPFY6Gd6n64z2vzyqz06c/FeLpCt
7TJdbutDHxIAJCTkF4UQ+cXo73LxmNv02nSkur1Aan+RjhesnlwaEPpVFLlH
l5wdjvc/M9xObHdar7juaOYf6d8/uQxFjaOG+4ptO3zfjpizZjrFfq8NVNcz
EnLeenT3Ti7fnqt/Njy2WJakyy/c6/pjd0XyGN4q+3Pp9cnm9VIbS9nlAawR
AwBJBflFIVR+MajX5Byglx+M84uvv6e0nEpLSwNwr+WL4zsKVP1Oesc/LfXd
FFB5eeCxSn2vSeNPwsovXnLa2qmhporKuf0LC/MpPzeXsrMzdI+jzAe1Q8YZ
ammmzT++RNlO5BmU2ob8sqmwuJzqWzto2OXWHCO6exde+Z6PXUza/qOuYP1H
7ANa59vuI3Vf0NO7wuuiNyg1bROV1TaTfYKJ+3+rAADBIL8oxJxf9NoxgueX
0MJvfwlHyPYX7yM6pDOHipedmx0yvwRtyxHH6qbvoEHFeBZ+LlFnfQXlZ2vP
y893uu2S2wyiu3dy+Rqdz0OWL2nyy1P9cS3a6wqScxbHqbm8gN57XWcO0t9/
RtcnAtcSAABIDMgvCq86v/DjM1iWvF5vEKHWQJHbXw7y84vYYMfyEht0/C5L
naVrpf6cE9f6fM8y5MsgjusRn7EQTfvLi6mWkO0bHn7NGVs71VfuknOIIu9E
d+/kexSsj+35yJkk6z+6S+lC1thnM173xjtwVMgkHwXNOfPMBNm6G2n/lk8U
OeYjuofxuwCQgJBfFF5RfhHryYz0AzQa8zV5qLkw9NiOYPdCKjf7SOrLaRzW
b6cINf5l8wm9saB+4rha5fiXYPj5TuLc6johd0R377jyCfdo2zm9MUp+ynHQ
SZFfXi5Sw7ofCM8HuGG4f9/+3/j3/6Q+7DEu7MQ1aW71vlsr43nsAJBcVlx+
0W0/ELyi/PLy5QTtF3JCUaP+/Gi+7q4sLaWyE50hx7RKY2DT99Ij3bk/LN1p
qPCNDVHON9aUW1qLxaDPintfnPtjOP+I2/e2zhwtfg6UeM3yOGcvddaUUGFh
KbXrPi/Tq9MvFd29m7om3qMd+uOJFNktefLLS5qV5jm/T60unet62in0MaVQ
TuuU4r0Fai7JpNTUddQ4qtfGtyCN+d19+4kp1wEAYKaVll/m7NVC/8N+ehRY
j72y/KKYz8upuOZQzbv2uO7RXmEsSFpJl+Ga/RLFnOL0nEM06H6hOn9f0x7p
XFcVa7poyy2uo8uvGdxCjCILeV0PVONijPOLf/287kk5J7HuR3RMen8D3XOL
90HOJ/z6L49UzwtgaeTaQWlMr7LcUd075Tp53Gd/TzGmhmXU15Y04194SyO0
Serr+YxuKbPjfD9tfV1+b0i1xoucT/j1X/rnlfd+kQYa8qUxvXhuEgAkopWW
X17MfKca45mbm0sVV4U158T8ErCOijK/6PV7hMovp4X8om7T8NDl0ky5LNkF
VFpeSoX5WapxH8HnHinKOHJRtS5+fnEplRYXql7bHvDMSr1yz0jr1/lzAz/v
KD8/Vz5uYU7Q/JJbmC/f2/x8bt981f0+2DOlLvdwi+r9/OL9VFlZrhrLu/7o
Xc09jebezfWfVX/2hcXcPZLX+c0rL/c//8hoHZ0IWJVf9OZJs86LimdVv0HZ
G7fQlo3ZqtdOOrTjcJ8O1KjG676btom2bNmoGsuL51YDQKJaafmFN9ZTq64f
xbpYzC/bL6j+/n4+Isyr3d6i+3f5SMNO1RgNNWHshW4W8VJf00Gd5/FkU0nV
ZZoIM7uIvK57dEhZhwuy8/fSJduUZnvH+a26Y24D748/I+ygc70z9EyYY6we
RyLnl3PDz2iq44imDHybzNUhg+dETt6mQ4U52n24c/Jrwui3P0V3754523Se
UbWBjl5yEPvC344V+PlHw8z84h2o8OeJtScMx6/4nmP0js4coh99Rq2jxnOI
vKPXaGvq29r9frzGtybMYpz/WwUAMLIS84vIN0eFTYC2cdZLbjfjexY2w7hD
jncJeV3Cc7V5bs2ztMPFksftJg93LLc71PhNnTX0uGvi92cYl+q51MGwXg+5
hXIzIc8Z273jy+b2cOdzh1e2SJmZX8K3SBMOG922Ochht5HNMRF2/lhcmCfG
xX1WPGb+FZcbACByKzm/gFnCXP9lBYlPfgEAWDmQXyB2yC+BkF8AAKyF/AKx
k+ctBVsfbiVBfgEAsBbyC5iB9Y25sWYsSTJCfgEAsBbyC4D5kF8AAKyF/AJg
PuQXAABrIb8AmA/5BQDAWsgvAOZDfgEAsBbyC4D5kF8AAKyF/AJgPuQXAABr
Ib8AmA/5BQDAWsgvAOZDfgEAsBbyC4D5kF8AAKyF/AJgPuQXAABrIb8AmA/5
BQDAWsgvAOZDfgEAsBbyC4D5kF8AAKyF/AJgPuQXAABrIb8AmA/5BQDAWsgv
AOZDfgEAsBbyC4D5kF8AAKyF/AJgPuQXAABrIb8AmA/5BQDAWsgvAOZDfgEA
sFZy5heWXM5hmmQ8cb9/oMa6XTQ8PEkedmV/zsgvAADWSsb8MnZ5J2VkZHA2
0G33UtzvIQjYUdqbke77bDKP3l3Rn7OZ+cXR3Ui1tbXU2O003m5hmtprd9O6
1FRavXo1reb+mb2xlFptk3G/FwAAVkjU/OJ1DdK11mtkc85p3nOc/kKo1zLo
0uSLuN9DEDy/TwXC55K+qy3m4yXz52xKflkYocPZb1JKSorfa3uJ0dlutu8o
rRK30fFa1gmaToB7AgBgpkTNL/aTfxT+jr+vfd8zSh3XrlFHj4O8CXAPQTZp
66Zr1zpo0PU89uMl8ecca36Z7K7SZpJfH6D5gO2WZjvpPfH9H2XQqbYBYubn
iZnop7qi30r7/tWX39FiAtwXAACzJGp+cdRv9eWXzXUYQwDJJ/r8skjtpb+Q
M8u7xdRUV+D/97e0+aXv8D8KbTPFNK5zvId1fxCO9T7dmk+uPjgAgGASLr+w
HnJ7GOos/9Tf/lLWRozHTQzDKMaEsuRmXNzr3oD9vb7X3R7W9//5saT9tl7q
7e2l/mEXsaptWWKcg2Tj3rPZbDTknA1ZNg8z6tu+17dPPzldkY4rVZePP55Y
vqHJZzGdj+XukYtxC9fIkmv4gW+/Xm4/l5sN2JahoX4b976NbP1DxHiDl9vL
3Uf/9kI5JpmAexlQDhcT0F6ivu6XXjc5h+TjDbvcBufW/5zV1/qS3C4nd5xe
3/X0DznJHcbYYWZy0H9/uH2GFOONWa5sjKb8kYs+vzymA+/4s0tmWQct8GUa
+JNBflmgE6v92/7TKYP/JpcGaZ2QhSptxt8fZmKIurvbqK2tm27b7OSaX4zp
+gEArJZo+UXsN9KTeVSoDzz3KZcfY5F1ijyKfZ85TvnbbOrvkr11n/YYWXvp
gYf7G5S5R3tz0zXvZ+06TdN6dR87Tc3lm3XLlFPWrL+PDrF8eTWd1FmzTXWc
tIr7MZzPQ6dz07j3C6h32Eb7s7XXVtL40LdtX8MeneNmU13vjLbMnlE6Xbpe
txzpOXvpHqMdkyJ+fsf757SfS919Gus5rn9dJc3asR26n7N8rfdcw3SyMFPn
eBuosd8gj3oe0bHCLN170Dg8RyPnN2nKH43o88scNWzcQGftT6XXnvYZ5ZeX
tOAa4bIblzcWDI63NEKbfPnlDTozwWreZyc6adN7+uNmfrezRXM+AIBEkWj5
ZdZ2iSqrKqVxoBnpO6iqpooqKyvpklgnPb9PO/h6Le+Mbn6RFVBNQxPVV26X
693cHbRDqN9zig9RU2sTVRbnyBmp7Ka6TOyoKg9srzxJ9fX1VFWuOGbOqbDG
R2rLl03F5ZVUWVpMJ3qmYjifh87np6mOnVd6kpqaTkjXyisszpfq94r6Jmqq
r/DlA7Es7co8wk7QIWU5yo9x96qV6qtK5POk76XRgCwl9vvp5RfldZdUnabW
1gYqV2SJtJIudbuO7uesvdb0/L1U39RKDTVllK14/WrgmF8uD32dobymk1wZ
mqiqNE+6L4X5WXHOL1rB8ksok1fy5P6jhYD+I+9dWiPllVX0ZXkd9505Rbuy
f60YN9PxSn8fAQCEK9Hyi2ikQRz/8lD7fhj5hX9P2U4xN3RRVedVdIypjulo
2inlJV8bjfC6veYL6fV2p7qPZ26oRar/iy6Nh7wmdfmO0SOPdjxCdOdT1+kn
VG0pT6i5WG6jSM+pplFlf5GiTlfe69kbB6QM2O1S5wDWdVvKl0d7n6jvY4j8
kp5ziAYD5kI7mvZI+aGbUbwXRn4pu+RQ30PPIO0V82mFeg73jUOfSue5OqzO
J8p7uxzyy+L8NLVXF0g55LfHtOPgpbExbxfTyKL6vZn2QinXaHIPAEACSNT8
Io3fPaFTB4TMLwXqelBwo9zfF5K+64p2/Ab7SKjHC+iemCuk14zrs6nru/3n
zKoO2QajLJ/ueiZRn0+u09frrLuyNNMmtUtccmr7fEaE7Ka81/75663U3q/T
r/RSzlmBn0/w/JKtbRPxmZbaek7YFNcdIr9klXTplk3MXnw7lTvgWHqZS9rv
zuGkzi8Dh3+v2w/08bE7utuL+eVXe3Tm+L1cIFvbZbrc1oc+JABISMsxvwS+
HnjMbXptOlK9WCC1v0jHy9E/ns/SgFAvKnKPAbl8F3SPF/355Dq9dkg7Dvil
d9C/T/oOGvRqy/jccdb4Xkf4+QTLL8bX5aHmwjRtbgiRX47361wrfz0jZzTf
AylDpR+gCcPrkvvMkjK/HPfnkddff12dYX78Hu1p1P43O9m8XmpjKbs84Bsr
bEZ5AQBehWWZXwzqSblu1av3jPOLfzxJOZWWlgbgXssXx1MUqPqd9IQqX/Tn
U9bpOvWuwf0KPK/2XnvJaWunhpoqKufOX1iYT/m5uZSdLfezmJNf9PcLnV8M
MobOfqGyY9jHDlO8+4/4ediu0VtUmvaWlGO+ap1Sb/P0rjQ3KUUY45uatonK
apvJPsGYUnYAAKuszPyiVzcFzy+hRdD+EkZ+iex8FuQX7yM6pDNHi5edm528
+WVXS5C50V79dqAoxD+/iBaoYd0PjPdfHKfm8gJ673WdOUh//xldnwhcowAA
IDEgv4iC5Bd+rAnLktfrDUI7NzVQ2Pkl4vOZnV9Y6ixdK411PXGtj1xuj++c
4rghcW3/pMkv9lqpDG6DMvjmZi+b9hcZ+7BGyCSf0dCi8XbzzATZuhtp/5ZP
FDnmI7qH8bsAkICQX0Ta/CKOo+DHTIyacE2hyhf9+UzOL+wj6TmMjcP6zwEw
d/yL9fnlxViLlMf0xnb7zN2S5iAlRX5ZeECb+LXu3t5GI0H2X5q8QG8IWSTc
NXjZiWvS3Op9t5Lv+d8AsPwlbH4x+Pve5xXlF348536hHi9q1J8fzc8lriwt
pbITnSHXbA1dj0d7PpPzizje16hPjHtfmnOdJPmFX9f2ZK44b+mKzmflpcul
8jzzZMkv6ULG2N2lP6eK1yM+j+Bt5fMfF6i5JJNSU9dR46he2+ECHRHW9t19
2/jYAADxkqj5Zc5eLfSl7Neuk/LK8os8t5hXcc2hmnftcd2T1hrRrL2mI5x6
PLrzmd1/JK5xy69J3EKMYh0dr+uBalxM8uQX9fzo9O0n6cHkHLEsS+7JB5o1
eZMiv7xcpObsH0hziA51OwP2naOew58q5lEPKt6T8wm//kv/PKs67kBDvjSm
V2/dXgCAeEvU/PJi5jtVfZKbm0sVV4U158T6KWAsg7Ke1BvjECq/nBbyi7rN
waP6uzwju4BKy0uldVr9/T07Qs49Cqd80Z8vxLgN7n4VRDh+d0Zav86/bgs/
7yg/P1d6Lb8wJ6r8YnTdQfOLar8wxqiI16tzPnmtPK2ssit043xRQucXzTMW
2EHapBx7+84a2lJUQkVbstTPr/6kXjN25ulAjWq87rtpm2jLlo2qsbxv7sT6
uwCQmBI1v/DGemopX7GG/XqxrhTrte3qubDPRy4Kf1u36NbTIw3+to06o/nT
/NwT3Szipb6mg6q16cV6vaTqMk2EkV3CKV/05/NSc7F/vO25Yf31X/j+HqP8
Iq7/ErguTuD99+epHXSud4aejfmvZds59T6O8/4cck6xDk041623n/7nHOJa
g3w/RHPD3VRVWsxlwnwuF+dTYXE5NfaM+N67U/l5wuUX70CFP0+sPaG/Rsvi
ODWUZOquXcc/N6CsqY8WjY49eo22pr6t3e/Ha3xrwhjtBwAQb4mcX0S++TZs
ArRhs15yuxnfs7AZxh3zM4oT7ny6WPK43eTxuLmyJPk4Tu5+ejzBrsEjjZFJ
pPwStsV5mnDYfc9T5zlGXWHnj8WFeWJcLnLxmPn4f1YAACEkQ34BiB1L14V2
m8yKm7rbzPaKz8YOMkcpTHHJLwAAKwjyC6wUM53fSP1geeWnqXfISYzbTS7n
A2qq2iW9l1kWeix2KMgvAADWQn6BlYOlvvoiw/G7vJyyZu0Y2SggvwAAWAv5
BVYaL/OIOprqqLK8nKp8z3bi/ll/2Tef2qxzIL8AAFgL+QXAfMgvAADWQn4B
MB/yCwCAtZBfAMyH/AIAYC3kFwDzIb8AAFgL+QXAfMgvAADWQn4BMB/yCwCA
tZBfAMyH/AIAYC3kFwDzIb8AAFgL+QXAfMgvAADWQn4BMB/yCwCAtZBfAMyH
/AIAYC3kFwDzIb8AAFgL+QXAfMgvAADWQn4BMB/yCwCAtZBfAMyH/AIAYC3k
FwDzIb8AAFgL+QXAfMgvAADWQn4BMB/yCwCAtZBfAMyH/AIAYC3kFwDzIb8A
AFgL+cVKLLldLnIxngQoS/RYj5smJ13kYXFfwoX8AgBgLeQXC3nuU25GBqVn
nSJ3vMsSA/vJP1IGdx1H+udwX8JkWn5ZGKeG8lxKXb2aVgs2lNTRyPxSDMdd
oL7Lp2hL9lrpmKlpm6istp1cC6H3d95upF2KfdOyN9Kxpj6aD7HfwsQ9qiv5
ktJS3/Xvm5pKG4v203X7TNw/LwBIPsgvFnp+n3bw9XTeGfK8knN6aKjnKl3r
6DM1Fzjqt/ryy3Gz8ssrvy+vnhn5hXVeovdSUihF1/t01uGN+JhLrk5a97rR
MXmrqMpm1C42TofT/jLIvhnU5dLLVYvUc/jTIPul0GtZ9SHzDwCAEvKLhV51
Pf3srq9dIyNjA93zxPL3uRryS+RizS9Ls52K7PIRnb3tpPmFBZqwXaR0RYa5
rpsXjIzTVim7vEE7a3togpmnhXmGBtqqaE3Q4y5S86a/kPJG5rfNNOpiaJ6Z
oPbar+gNcd8fbqORRfV5J6/kSfv9cO1e6nJM+q6Fmein41t+K7335s6OuH9u
AJA8kF8s9Krrae+g73wZGQX0wIv8Ek+x5pcrUlbIoFuBfUXeu7ROzAuZLbQY
5jG9fX+SssuZUVbn+yMf97eHBlXvsc4aKWfs7vpee+yHNVKG+arrieK9OTrw
jv/1v96gX9aB43+QrvXegnnfWwBY3pBfLCTW0zlyPc1MDpOtt5d6bTYaGp4k
b8jjeMnlHPLv02uj/iEnMR5t3eNxu4kZ+46yhfaXq85ZcjMMMW6jvgAvTQ71
c8f0H5cvi9H4XDm/PPP9f6/bRUNc+f3lGSaXTnnCui9B8ouX+7u+31e2XrL1
95Nzkgl9XK+bnEM2/z62fhrm9mFD7ON2Oblte6Vr0bu30Ygpv3A5Yo2UFZ7o
buPtq5DaSjT5xqhMx3/vb+f40ridY+DwP/q2+dWeO6rXn/Z+7T/fr48Y9vP0
FP1Cuy93LelCv1SrUVuRdL3vU1dM43oAYCVBfrGQWE9vbyGGeUD7c9N9OUAl
/Wtqdz7X3X+sp1boD9IqOTcg183P7gq5RU+2pi9pxnaRCgy2rbjk0JRDzC/n
+seos2qb7nkqLo1Gfl/08gs7Tc3lm3XPkZ53iB4wL3SOyVJf0z7968/i7+8z
zT6s6x7tz0/T3Wf70c6Y24ViyS+zPYVCNvmCRgy3k/uCClqnwjqus2F9yH4a
w/xiP0Npq1fT7tYxw3379v/Gt+9PlPuyg7RJyC/XGYNswiK/AEDkkF8sJNTT
fJ0o5ouswv1UU1NPNVUlqtxwNSDDzHQckN/P3kFV9U3U2lRPpflyBtpzady/
PVfnX66qosrSPLkOLj9GVVWVVFl1mRhFu8rY9W8U5y2gqoYmamo4QYWKbLW9
7r6qLGJ+UZanhtuvteGoKgcd7NVvKzC6L5r84n1E+zPkcuSVHqOm1laqr9yl
KnO3S51hHOfl8uUUH6LWax0BZdtA3cq6U+pn879XUX+ZOjpaqUpx/zIr7sb0
2ceSX3pLfyH0t3wXdDuxveMnAVnDiHdAbLNZRY16/UcLD6T+o49PRfrf+Bwd
Wa2Xpxak198y6j+qE/uPPqP+ReQXAAgP8ouFFPnF10ZxbUT1Pss8oL3Z/vqa
72OS5ww9pkNCPb7+6N2APhCW7tQIbSBZ1cQo31t65D9f+g4a1OsLmrsltedk
lbSo9+WOa2/aI+UpZX2vzC/bT9wI6PN6TOcL04T2kQvhtVsY5Je+qs+lTHFp
SD3Whm8v+Vq4J6rzsKO0V3i9oj2wHWKaTub6y7b+xEPp9bHW3cI9r6aJgPs0
e+ewVIZYxhDFkl/EdozANhDtdj8PazvZAjWs+4Fi/G47jU64yOWaoL7LlbRG
HNv7WjGNR1hmZ3OedNyLE+psxI+NEcfO/OjDYrpud3LndNHE6D3V+N38tvDa
kQAAeMgvFlLkl80n7utuszTzndQ2c2lSbFfw+uZBt7b20LReDuGOWyC0Raj6
hqTzFejOPxpp2inknm9pWrfMT+i0UN8fsc1Lr4v5hc8bevOy5WsooAfhzHvS
yy/eQSmfHOzWb8d5MdUit1eJ90rKL/pjlr2uQerp6KFBl9y+JeaXzYpMI+Pu
fW8P9fQ6YupDMiO/ZIZoA5nt+VroD7oRwfG5DLPpfwkyl/nrIH1W+ljnaWns
7sfHBnW38T48I89R0lEQpF8KAEAP8ouFpDyRTe3/f3vnAhzVed9txpPJTGY8
08zkq6fTyTf9kiZO3KTp5Wub2P7cuNPEyaSJm8Zp02CnbWzjXmJwUoOdGhxj
hDHCGAFG5iZjhI3NxUbYAiRAgLjZ3CzZEiBASEgY2RIIJCQigRH+f/vfs3vO
rnZXWknn1dl393lmnkks7eXV6sfuT+95z3tSHfsPfV5uzn/QOR607VR6j9vp
9Zf3UvSXxB7RKesj6z2erXg/9WP3dkt3d3fcnE+0vzxdmmJ8sec9DbO/XKx7
NbIeaKE0pbxvt2yMzPUs2hPd86zJPeY0sWCtnGhLvpYo1g92zXfnWFbvrU9j
DfXQ9aO/zN4/8PE493jQfS9LV1qPnbgPyzfvvDu8n1xst/j+I2v6zc2lVs/z
ds+7/ueXk67tDe85882YvvLHt8vY+++XO7/5Ve9rX/17WV511vffAyJmr/QX
g0b7xPgVKeY7HKPrNx57Of7zrrftpOwsXyfLlxRKfn6eTJkyRSZNmBC3FmQ4
/WXV0cT1rAMZ7S8p7zfg86a+fbL+Mtg51dHX6uGY16o+Mp8SdcKk6VK4fK3s
rKqX9u4kj9N5xD3mFJ3PycsvlDXlO+VES7svv/vROH50LLJu5HsLks/t9beh
5D/dvnDvgo3xe+32XJDqdbPdHvP/frN18POyY8/jHvM/crQnyW3c9bshv/KA
lNY2x33/QtM+KRj7ZXddzptNQ9+TDxFzU/qLQd3P6YHXhUT7QWx/ady2KOX5
RBNG2F9KTww+R5FsfCn3f/Gzv8zcMuB8SLLXSj17tFKW5E9O+prNWX0w8TF7
z8iuNYtlyoTEc8LGTZwr+1uG9hr114/+8r0Fg61/Sa/nOD/vEbdr3Ls0dd+J
HpPSLjHguUA99TF74SXZoyai15kG2tulVZ6/M7qH3VCOhSFiLkt/MWj0c12P
iQxw7cPoZ3J0TkHXk7jn0xS8IlUNLdKpx3R6e93HHc7xo7WR/hLdxyVdR7W/
TBxk/iVFf3Ht7Qzvl7OzfLXMijmn6sl1qc/v7gzvZ1MZf56TroEOaP3u4Rf+
ddC9VnQdy0tjx6Q//9LxdmQ/3x/KvgH3iPP2m0t9/OqM2zd0b+DdKY+NfiQH
ImuMBxujt7/MQq4jgIhpSX8xaMz63bKGZPuWqOfcXhE9/9g9P2bmpuRzEcPq
L97akSdXJ1u36tjb2SYtLW1xe9mNRn+5VP9apDfMGqA3tLrnE8WuL06td65W
unv99rbsd39nq4fY82IdSX/R9bDROZCUe6Z0v+1eX2B5OtdBcvvLPYP2l2g3
Sd5fzstL47xrJZU3DbzfnzeXNHB/cfcGvm1u2mtvEDG3pb8Y1O0ZD8j4FMdF
zlevcNeSVkb2ZnPXeLyY/PPPPY+of1/oTHFeUkR33eq46Sl6xhn3vO1k5x+Z
7C+x63Bnppgr8V6rCVIZ2QOmu3mHFOTlyZwXdyXda/dypBeNmxi91nW37Fo5
R/LyCqSyOVmn7HaPs43kegkju37AGZn51YGvCXRgzj+61xs6lc5jdr3nXjfp
8dLU5/p0H35xgGsMdEnJoze7338ljd4U3fM3fF2klLfrktX3fzF8u5uGcD0E
RMxt6S8G7bf/y+TF8XvJfVD1uruWZdzMHe7n78U673N6Xc0HMY/ZLbXlseti
+vcF7/znBf32mgnbe9w9R/mB8XPlndg1Ht1nZPuSx5IeOxmd/hLby0LjL62N
63unD6xyX6v7F+x2v+7O24RcvLPf/jrtR2Rp5BjS/XN2R15fr5/o/i/H464X
0Cv17rqjCVLRkmrObHBHev2j5o0Pu2ttHyyOX99yuMT7XuI+c+dldWSPl5vG
r485L6lHNk7w9n6ZvflwQk9oOfyady7Rbfn91pz3SGVkXz31uf1OLnt6ehKN
/R24c0khfzpXatr6daKeM1LytLcHzFPbE6+thIiYTPqLQSPzL+MmTZd8d9/c
CZJfUCB5U8bHrLWYK0diP/d7m6Q4Zl3phElTZFL43KPo/rePR/ah6z/P0iu7
Cu7zHnfCJJk0uVhOxnSmS42b4q41MCkvX/LzpsStX326NH7+Y9D+Msi8T8rX
ZWL//WQ6ZXPBg3Hj13OupsRed2F8kZzsHug+j0vhkiVSGLeW93HZH3PdgYsn
NsX9vFPyn5clSwrj1vLqvoEj+d2PtL/onMTGqTe7n+tfGfuQPPHEE/LQ2Nvc
r8X3k4gdu+T2Md7xnbg1uHoukLvmVs9Zvjv8mOq4O/8o5rzq2xP2oOtwr/0Y
PQc69V4ueowqdq1uQ0zfUn864dfO8z56X9x522md84SIGJH+YtDIvijjpumx
o3OyefnMuM/N8JxM4XppSnaOb/dJWVuQeD7NtNDtz/SGPrPz7ku+ViThfomd
QveyXZo3PuGxJ0yZKxVHP0gYS/R4Vsrzp3uPO+cjD7h2JcnrkvS8LN0HeFHS
6znNWbMr6f552mEOlixOeq0ofb2OtyfOo3Q37w+9BhMTz1eaMD28J8xg130c
zJH3F7VH9hZNTNoR7l2wM8WeL63yQmRdr+4Lk7AWtueMbJzzYMq95H76m5fk
aJJzibzrRaZj4rlGes2th+I6UnyPKt6Rek0WImIy6S+jbKh7tLd3Smd7m7Sn
ca3j3u7o7dulM1nPSfk8kX3oBjjvqbuz07lGdZuOJdP23egO/dyhnzk0xrZ+
64lT2+tchzvyM6Vzn/DrG7l96mt1D11/+otjz4VTUrV/v9SdrAv9b5U09T8G
Mxx7uqQp9Hi1tXVysq5KqmpPSlvXyMc6mF1tp6Sutjb0s5yU2qoqOdmUxnXF
ERGTSH9B9F8/+wsiIiZKf0H0X/oLIqJZ6S+I/kt/QUQ0K/0F0X/pL4iIZqW/
IPov/QUR0az0F0T/pb8gIpqV/oLov/QXRESz0l8Q/Zf+gohoVvoLov/SXxAR
zUp/QfRf+gsiolnpL4j+S39BRDQr/QXRf+kviIhmpb8g+i/9BRHRrPQXRP+l
vyAimpX+gui/9BdERLPSXxD9l/6CiGhW+gui/9JfEBHNSn9B9F/6CyKiWekv
iP5Lf0FENCv9BdF/6S+IiGalvyD6L/0FEdGs9BdE/6W/ICKalf6C6L/0F0RE
s9JfEP2X/oKIaFb6C47cXmlraZaW9s60b9/e0iItbene3j7pL4iIZqW/4Ijt
fFcmPfCAjBv/qrSbuL2F+tZfuk5JSeEkGXvnnXJnxEfmrJb6C1eH9DgdJ/fJ
ulXrZN26NNywVy7E3b9Hqje/Pvj9Nh+WngHGULenVFatWiWlexoC//0gov3S
X3DEXnpXpmsfmfyadJq4vYX60V96G8rk78eMkTFJ/aG8Xted9mPtnfkHKR4n
mbfL7rh+dF4WfjOd+82StmTP31UvL0y41bvdTXOT3w4RcQjSX3DE0l8SHGl/
uXp2V0x3uUde398gF7q6pKnqTRkX02G2t6Q3D9NRt1tWrFgVnv9I6rp1UnB3
9HEfkHe6Yh63+1DkOe+RBavWpXiMFbKqtDph/qV5z3K5vX/P+f7CfvM7iIhD
l/6CI5b+kuBI+8uWX3/e7RL7+h8rCvWJh6Jd4MFNAx6zSd8ueWnsl8KP+b0F
7/Z7vrfl7nDvWCZdaT9ej1QWfNfrLD/Ilw2rH3f+//+jvyDiyKW/mLBb2tta
pL2zN/zfnW0npabqgBw4cECONl9MuH13W5PUHHC+X1VTIw3Nbakfu7db2lra
pL27N+VtejvbpaWtXboHGNNH3e3ScLTKec6qGjnR0j74zxW6z4mayH1qjobG
GblPqI887nN/GdJrEjO+uJ8pdJ/eQe7T3tIQuq0+T5XUHD0hbZ2pX9ehOKL+
Euond0c+92fvPpf89ale7M7BJPSbYdhxYJY717OvK/7xrp7d5swF3TaU4z6t
7jGnBxfsDPee3sPz6C+I6Jv0F/+9WPeqPBD6fJ68cpfsWvlk+P9HvX9xzN+2
vWdkY+Fjcd+POm7yUnmv7XLiY9euCH//wRdTfTZ2ytpJ94dv81LNxYQxPbb6
XWnc+1LS55w4Z2PKzye9z4Qk9xk/Z4t0Xjri3/zLMF4TPZ+pesNzSe/zwPhZ
UtmQ2Bl7W96R56fcn/Q+017cNeJ5oZH0l7N78yJd4n+kPuXtTsnUP3b6wePl
p0eY2VYpiHSNn/Sfe/lIu8388Pe+/MjWIcz1nJeSRx+R12s7vMeppr8gon/S
X/w32hU8J0h+4RJZUpAvL++NfNZ0H5fnHxjn3mZyQbFsKC+XNUtmxtzvcdnT
cjnpYz/2cur+sn5KtL+cH3BMc5avlfLyEinMG+/1qzm7E+Ys6stne/cbN12W
r1wpK1cul+kTnPFPyssLd5sR95dhviZ166d6HSx/qZRv2ynlJS+G54Scrz8i
e9pi13M4fSv6vcVrNsvOneWyvGCy+zgPLj40ogyMpL8ciBx30b4w0O32Pu3c
7pZnD45orGf3pp57UaNzPT9ZekS0l+zf/LoUFa2QFStWyLoNO6SupSOt56G/
IKKf0l/8N7YrjJtcLMc7Ez8Tqpf/t/v5WXb0fNz3dG5gVuRzfNzkN+I+4/3o
L+MmLpUj7fFjqtvwbPLP+vP7wuc6O3Mtm/rNz5yTzYUPx/ysI+svw3pNek/K
3MjXF1f2n4c4I69E5qIefvmY+/XGSB8bN3GFNPXGj+3swRfcMbzXPfzjMiPp
L9XP/2P4c/7vBukl1c9/J63bDeyZAede1GOr/8s9VnX37cnPPbpt/DI5Nchz
0V8Q0U/pL/7rdYXHZX97ks/A0N//0c/iRXuSr2+4fHqTO09S0Xw54bGH31/i
H8/zjCyNzKe8XOXdr37DjMhxmCI5k/T5WqV4UqRXTBxBfxnua+L2l8eT9o3u
liOyd+deOdJyyf1atL88FtNpPLvl6IG9svdA3YiOIfnRXx58deB/Z9F5k1tn
vDXscZ6tzHPnXt5JMvcSO56oP33iBdmxZ7/s2FAsv777Ju97/7xswPUx9BdE
9FP6i/9Gu0L/uZP+339g3EJpSvk43bIx7/7I5/kHCfcdbn9J3TE63efz7uc9
1rMV76f8eT/YNX/E/WX4r0mTe8xpYsFaOdF2adDnj45X51hW763vt87ZH/3o
L7P3J+9xUbsPR9bw3vfyEM4LivWMzPxqZO5lafK5F/VAwV9FOsrXpHhf4pgO
l0xxO8zE0tRrcegviOin9Bf/HawreP1m4M/76LqOh2O6irn+Enq+NVNT9pdV
RxPXwEa91PjmiI8fjeQ1iVufE3LCpOlSuHyt7Kyql/buJI/TecQ95hSdz8nL
L5Q15TvTOw8rDUfj+FH0uE7C+c5p+kHlY4POvYRvV1UuK4pWSHnt2ZS32TL1
G5G9XZal7Cb0F0T0U/qL/6bdX2ZuGfBv/2ifeCwD+ktpwwDzGt0jP/9oJK+J
evZopSzJnxzXY6LOWX0w8TF7z8iuNYtlyoRxCbcfN3Gu7G8ZfB5nIP3oL99b
MNj6l/R6TnK985cGmntJV3cu6Kb8FMcZ6S+I6K/0F/9Nu78McrxlwP6yOtna
DdXf/rJ2SuK52P29VP+ab8ePhvOaxNnbKS0NR2Vn+WqZNcnrJk+uO5nyMTvb
W+RoVWX8eU7jpsuRgNbvHn7hXwedy3D2mxsz7PmX5i2T05p7SduOtyP7Bd+T
cj8a+gsi+in9xX8H+yyOft4/MG7WAJ+Rre65M8uqLiQ+dsp5inPu/XyZf4ms
N3lyXaq+9JE0Rtb4jqS/jOQ1SW2vHIzsv5Pu3FBvy3733OrVA3S2wRxJf+lt
WOteh2h7W4rXovtt9/oCy4dwHSTHocy9tMoLY51zj8oHuFaBu//dAN2E/oKI
fkp/8d/Bu4K35nRminmB89Ur3LUZlTH7nUT3r3tg3Fw5mfS5X3fnEEbeXz6S
09vmu/MR7yU5D/yj3uPuWpIRnX80zNeku3mHFOTlyZwXdyXda/eyOzcUvdZ1
t+xaOUfy8gqkMul5WN1J56+G6siuH+Ctq711xs6ktzkwJ3JO0B89Oeh5y/1t
3vhw8uscJfW8LLtzTOQ4VarznM5HOo6eg5R6LTH9BRH9lP7iv+l0Bfe85JAL
Smvj5lJOH1jl7nV7/4Ld8fe9eMjdl23igi3SFrN/ydmjm2L2bPOnv8Tt9Tb+
eXknZl1Ib9t7sjTmGM1I938ZzmviztuEXLyzPu55etuPuOPz9uXz+onu/3I8
7noBvVK/bZF3jnZLsn6TniO9/pHXMcbIg8Xx61sOl3jf+3nCOdbnZfVDXwh/
76bx6xO7xNV6+fWY6NzLkbTG0rD6P2PG8lb8Y/acktW/vsX9/vLa1OuG6C+I
6Kf0F/+N7QrtKW/XKZsLHvTWW0yYJFOmTJEpMX1A91w5meT8mdq13n6z4b19
Cwokb9KEhHWoqfpLqjEl7S8hz9e8Hve4k/LypSBmrezkwkLn+kcD/rwxRq+X
lHD74bwm/e/zuBQuWSKFcWt5H5f9MdcduHhiU9zPMyX/eVmypDBuLe/DLwa3
/65jl2ycerPbC74y9iF54okn5KGxt7lfS9pPOnbFXO/5dtndby1KQ8lQ5l6i
ep0o+riPPlEgTz8xXr4Wsy/MT5YOvI44tr+kfx0lRMTk0l/891J95HziaZsG
mY/oldoNi5JeV2jOml0DdAHnfv3vM2HKXNnT0CzbI3virjtxcUhjip6bvC7J
udIXG3bI3En9z9V5RF4sq5Pey8fDe8+Nm5Z8v5sE3fOVkt1+OK9JpxwsWezu
ExzrtML1crw9cR6lu3m/LM2bmHD7ByZMD+8JM9h1Hwdz5P1F7ZG9RROT7nd7
b+SaiIn3afWO5dz3cr95Du9Y0M+L05t7ib1v5YrH4/qK61fvluI9zYM+xsj3
q0FE9KS/ZILd0t7eLp2dneFrS3f2pnm/Xr2mdJu0hWxvH+oazuHZGRpne2ic
Ot6Rfsb7/5r0hsfXFnlN0rlPb3en+xq2tXf6Nn5/+otjz4VTUrV/v9SdrAv9
b5U0tflzjezh2SVNJ2ultu6k1FVVSe3JliFc0xER0T/pL4j+62d/QUTEROkv
iP5Lf0FENCv9BdF/6S+IiGalvyD6L/0FEdGs9BdE/6W/ICKalf6C6L/0F0RE
s9JfEP2X/oKIaFb6C6L/0l8QEc1Kf0H0X/oLIqJZ6S+I/kt/QUQ0K/0F0X/p
L4iIZqW/IPov/QUR0az0F0T/pb8gIpqV/oLov/QXRESz0l8Q/Zf+gohoVvoL
ov/SXxARzUp/QfRf+gsiolnpL4iIiGib9BdERES0TfoLIiIi2ib9BREREW2T
/oKIiIi2SX9BRERE26S/ICIiom3SXxAREdE2M7W/TJ06FRERES01Cv0FERER
bTHX+wuA35ArMAn5AhPYlCv6C/0FzECuwCTkC0xgU67oL/SXrKevR9pbW6U1
ZEdP38hvF6KrvT18u/aOnpS3IVe20iddHR3SHvodt3d0yUBJuNLVEc5Ba2u7
XBnwIf3PIPmykL4r0tHRHs5WV8+AiUk7W35n0KZc0V/oL/bSJ4eKp8oTs8sl
VYvoqN8hs/sdK125p3HYt5Oe01IyL/52M4orpD3J2wG5so0rUlv6gszof3x9
RpHsa+xKetv44/AL5VBr4ieI7xmMQL4soq9VyormJa7dmF0s1QmZSTdb/mdQ
sSlX9Bf6i2309bRKXfUhKVsZeT+YV5a0v/S17nN/vwtXlkpFabH732uq24d8
u9C7gJTOdr7+xLxiKasolYUzIu8HRXsS/vYhV7bRI2WR3+/shcVSUlri/X6n
zpO6mApzumJh5OuzZU1ZhZQUzXZvVx8TRv8z6EG+LKKn3u0PC4vXSknJSq9P
PFEkp2P+/kk3W35nMIpNuaK/0F9so6dubfzfHCn6S12p028Wlp10v9ZRWxK5
T4V7n3Rvd6WlMvL3eIm4/+qvNEpR5D2ktt+f6OTKNrpkx5oSqWu/Eve1ioUz
wr/L0vroL7hVVk59IvS1GbKnJXrbPtlX7NyueF+re2+/MxgL+bKIUH9Zs7JS
PoyNVo/33lHdEf1iutnyP4NRbMoV/YX+Yh09LVJ9qFpqa/dL8YxUx4+6In9L
9+8VHbJmhjPP6vyNku7tvL93+v/NUh95f+j/dXKVHdSXzI58JrSE//tKyx7n
fWPhzrg5t77o1925OP8zGAv5sp0+qQwfi54h+1qdCZh0s+V/Bj1syhX9hf5i
L1ekYl6K/hL6e2eeHueZXSodcd/ok+qVM7x/z+neLkRj2cLI3+Hxz9Zzssw5
5lBaH/d1cpUd1JXMi/u9R3/f88r6rR+40ijPT3XyGI6MgQzGQr4spa9PrvR0
SP2eEmetVcx8brrZ8j2DMdiUK/pLzM//2/Minc0mXmYwQk/q/nKlPvzvONmx
Ja+HdKV/u9B3Kxc6x5b7/3vvaYy8l9Bfso6exkp3jULjlejXkv++o58VbpZ8
z2A85MtGvDVW0Vy1xKx9STdbvmcwBptyRX+J/PxHXxd55gaRZbeJfHzN1MsN
vjKy/lJ5+kr6t3PnYeclzLdG30sW9vtbyKb3AUikr/Udd41laZ3312vqz466
IX92DC2D8ZAvG+mTk/sqpLR0jRRFesyMokqJNoh0s+V7BmOwKVf0l8jPv2lC
6MUY4/jWHFMvN/jKAP2l/98hMdSXzfP+3aZ7uxC14XUQ86Su3w2vNFYw/5Jl
XGzc43aXNYda477nfnbErIcM0/+zwkAGYyFftnPFXW8bnQNJN1u+ZzAGm3JF
f4n8/B/9VmTeF5z+Mv1TIu3HTb3k4BsD9Bd3fX5x3Pxs9D7ePEq6t9O/V+LX
QbjPtG9l+OtFO07Hfd2m9wHwaD0UOTdj6gypqOtI+H70s2N2SU2/b9RF1hpE
1h4YyGAs5Mt+vPeU+P4yWLb8z6CHTbmiv8T8/M27Qy/IdU6HeeEWjiNlPH2R
/lKRZN/JPjm0MvK3TezGHe2HnL+rZ5RE1rOlezuRrrpSZ7535aGY5+mSssh+
dnta4zexs+l9AJQeqS6N7KnxVLEkqS4OkTWSsWtilNOVRf3WVPqfwVjIlz10
na6T+tb+JbRdSiPvHe4alHSz5XsGPWzKFf2l3/lH5b/yjiPtne33yw0+0Nde
J2WlpVJRFtk/bsZCKS0rk9LSsri9O66crnT/jl5TsUcO7Slz5lKneufCDuV2
+rfMmsjX560sk32H9klJkfPeYPs+CqDndJR66ypnF8ualSuluLg4YpG8sHaf
+zuOnjM/dXaRVO47JJXunmCxe3mYyKAH+bKH+hLnfUL3RSytqAi9d8XsjThj
jcT+6ZNutvzOYBSbckV/6ddfPgq9Q83/otNf8j4pcvao3y85jJDo3Gky+x/b
aa/bmrAf/MrK+oTHTPd20tUoa2bH325GUZm0cv0A64l9n0+WLW9OXumRQyXP
97vNQtl3OvFAj+8ZjEC+7EF/twtnJ+ZqdlGpJEYm3Wz5n0HFplzRX6Ym/r5O
7/WOI838TGgwG/x8yWG06euJXN9s8GvnpXU76ZOOdud2re1JNuaIYNP7AAyP
K13taV87z98Mki8budLTFXrviF6/ceDfb7rZ8juDNuWK/pKkvyiVT3rHkbTL
bHlE5NpVv152yAFseh8A+yBfYAKbckV/SdFflMNrRGb8jtdjlt0q0ptqUR9A
PDa9D4B9kC8wgU25or8M0F+U8/Uii/4spsP8tcjV3pG+7JAD2PQ+APZBvsAE
NuWK/jJIf1GuXhZZfZfXYVb9iHOrYVBseh8A+yBfYAKbckV/SaO/KNphlv+N
12FK/324LznkCDa9D4B9kC8wgU25or+k2V+UyxdFFn3N6zA77Pk9w+hj0/sA
2Af5AhPYlCv6yxD6i9L9ocjcz3kdpqpoqC855Ag2vQ+AfZAvMIFNuaK/DLG/
KO0nRPJ/1+kvT35C5MTGod0fcgKb3gfAPsgXmMCmXNFfhtFflPf3Odd51A7z
1PUiLQeG/hiQ1dj0PgD2Qb7ABDbliv4yzP6iHHvTmX/RDjPrBpELjYPfB3IG
m94HwD7IF5jAplzRX0bQX5SDi7y1MIv+lL1hwMWm9wGwD/IFJrApV/SXEfYX
Zcskr8O8cf/IHguyBpveB8A+yBeYwKZc0V986C/X+px9eaMdpnr5yB4PsgKb
3gfAPsgXmMCmXNFffOgvStcHIs/c4PQXXdfbWjPyxwSrsel9AOyDfIEJbMoV
/cWn/qI0bvfW886/UeTKJX8eF6zEpvcBsA/yBSawKVf0Fx/7i7LrKe840sZf
+Pe4YB02vQ+AfZAvMIFNuaK/+NxfPv5Y5MVvRjrMdc6cDOQkNr0PgH2QLzCB
Tbmiv/jcX5QLDc6edtphCj4ncqXb38cHK7DpfQDsg3yBCWzKFf3FQH9RDhTG
XKv6P/x/fMh4bHofAPsgX2ACm3JFfzHUX8LHkf7W6zANW/1/DshobHofAPsg
X2ACm3JFfzHUX5SOUyIzIseR9JrVH/WYeR7ISGx6HwD7IF9gAptyRX8x2F+U
2ONI26aYex7IOGx6HwD7IF9gAptyRX8x3F8+viay+C+c/pL3SZH24+aeCzIK
m94HwD7IF5jAplzRXwz3F6XlgHMutXaYFd82+1yQMdj0PgD2Qb7ABDbliv4y
Cv1F2fCf3nGkw6vNPx8Ejk3vA2Af5AtMYFOu6C+j1F96O0RmRa6PNPv3RS53
mX9OCBSb3gfAPsgXmMCmXNFfRqm/KNXF3hzM1kdH5zkhMGx6HwD7IF9gApty
RX8Zxf6ivHCLt5ZXz6+GrMWm9wGwD/IFJrApV/SXUe4v7+/z1vKu/cnoPS+M
Oja9D4B9kC8wgU25or+Mcn9RXrvbO450+q3RfW4YNWx6HwD7IF9gAptyRX8J
oL90NjvHj7S/FH1jdJ8bRg2b3gfAPsgXmMCmXNFfAugvSsVj3hxMzauj//xg
HJveB8A+yBeYwKZc0V8C6i96/vQzkfOpC/5A5Orl0R8DGMWm9wGwD/IFJrAp
V/SXgPqLcmiJNwfzdkEwYwBj2PQ+APZBvsAENuWK/hJgf7nWJ/LcjU5/yf9d
9rTLMmx6HwD7IF9gAptyRX8JsL8oR17z5mC2/ya4cYDv2PQ+APZBvsAENuWK
/hJwf1EW/6XTX566XuTS2WDHAr4ReK4gqyFfYAKbckV/yYD+0lDhzcFsmhDs
WMA3As8VZDXkC0xgU67oLxnQX5Tibzn9ZZpeV6Ap6NGAD2REriBrIV9gApty
RX/JkP7ScsC7rkDJvwU9GvCBjMgVZC3kC0xgU67oLxnSX5TVdzn95clPiLQf
D3o0MEIyJleQlZAvMIFNuaK/ZFB/aTvszcG8fk/Qo4ERkjG5gqyEfIEJbMoV
/SWD+ovy2tjIWt5Qjzl7NOjRwAjIqFxB1kG+wAQ25Yr+kmH95dwx5/iRdpg1
/xT0aGAEZFSuIOsgX2ACm3JFf8mw/qKs+5k3B9NaE/RoYJhkXK4gqyBfYAKb
ckV/ycD+cr7em4NZ9aOgRwPDJONyBVkF+QIT2JQr+ksG9hdl/b3eHMyH1UGP
BoZBRuYKsgbyBSawKVf0lwztLxcaRaYxB2MzGZkryBrIF5jAplzRXzK0vyhv
3BezDua9oEcDQyRjcwVZAfkCE9iUK/pLBveXCw3eOpjVPw56NDBEMjZXkBWQ
LzCBTbmiv2Rwf1H0WgLRORjd3w6sIaNzBdZDvsAENuWK/pLh/SX2XKS1Pwl6
NDAEMjpXYD3kC0xgU67oLxneX5TY/WDYk9caMj5XYDXkC0xgU67oLxb0F92T
N3pdpNfuDno0kCYZnyuwGvIFJrApV/QXC/qLor3FvTb1iaBHA2lgRa7AWsgX
mMCmXNFfLOkvZ494czDrfx70aCANrMgVWAv5AhPYlCv6iyX9RVl9l9NfdF+7
jqagRwODYE2uwErIF5jAplzRXyzqLx9URdbxhiz9j6BHA4NgTa7ASsgXmMCm
XNFfLOovysrvO/0l75MiXS1BjwYGwKpcgXWQLzCBTbmiv1jWX97f583BlP0y
6NHAAFiVK7AO8gUmsClX9BfL+otS/C2nv0z/lMiltqBHAymwLldgFeQLTGBT
rugvFvaXU5XeHMzWR4MeDaTAulyBVZAvMIFNuaK/WNhflGW3Of1lxvUiPReC
Hg0kwcpcgTWQLzCBTbmiv1jaX+rLvTmYHRaOPwewMldgDeQLTGBTrugvlvYX
ZfFfOP1l5mdELncFPRroh7W5AisgX2ACm3JFf7G4v9SVeHMwe/KDHg30w9pc
gRWQLzCBTbmiv1jcXz7+WKTwq05/eeaG0C+vJ+gRQQzW5gqsgHyBCWzKFf3F
4v6i1LzqzcHsmx/0aCAGq3MFGQ/5AhPYlCv6i+X95VqfyPwvOv3l2c+K9F0J
ekQQwepcQcZDvsAENuWK/mJ5f1Gql3lzMIcWBz0aiGB9riCjIV9gAptyRX/J
gv7SF3pNC/7A6S9zPydy7WrQIwKx630A7IN8gQlsyhX9JQv6i3JwkTcHU708
6NGA2PU+APZBvsAENuWK/pIl/eXqZZHZv+/0l+duFPn4WtAjynmyIleQsZAv
MIFNuaK/ZEl/Ud6e683B1K4KejQ5T9bkCjIS8gUmsClX9Jcs6i+6/8usG5z+
UvjHzv4wEBhZkyvISMgXmMCmXNFfsqi/KLoPb3QORvfnhcDIqlxBxkG+wAQ2
5Yr+kmX95Uq3cz0k7S+L/jzo0eQ0WZUryDjIF5jAplzRX7KsvyiV07w5mGNv
Bj2anCXrcgUZBfkCE9iUK/pLFvaXyxdFnv6001/0GtUQCFmXK8goyBeYwKZc
0V+ysL8oO6Z6czDHNwQ9mpwkK3MFGQP5AhPYlCv6S5b2l96OmDmYrwc9mpwk
K3MFGQP5AhPYlCv6S5b2F2X7b7w5mPqyoEeTc2RtriAjIF9gAptyRX/J4v7S
c0Fkxu84/aXoG0GPJufI2lxBRkC+wAQ25Yr+ksX9Rdk2JWYOpjzo0eQUWZ0r
CBzyBSawKVf0lyzvL7FzMKyDGVWyOlcQOOQLTGBTrugvWd5flNh1MOwHM2pk
fa4gUMgXmMCmXNFfcqC/9HZ65yIt+jOuizRKZH2uIFDIF5jAplzRX3Kgvyg7
p3tzMEdeC3o0OUFO5AoCg3yBCWzKFf0lR/rL5S6R/N+NXJv6qyIfXwt6RFlP
TuQKAoN8gQlsyhX9JUf6i7JnljcHU/Nq0KPJenImVxAI5AtMYFOu6C851F8+
+q3IMzc4/eW5G0Wu9QU9oqwmZ3IFgUC+wAQ25Yr+kkP9RXl7rjcHc2hJ0KPJ
anIqVzDqkC8wgU25or/kWH+5elmk4A+c/vLsZ0O/8J6gR5S15FSuYNQhX2AC
m3JFf8mx/qJUF3tzMLtnBj2arCXncgWjCvkCE9iUK/pLDvYXPfdIz0HS/jLz
084eveA7OZcrGFXIF5jAplzRX3KwvyjHS705mK2PBj2arCQncwWjBvkCE9iU
K/pLjvYXZdltTn+Z/imRi2eCHk3WkbO5glGBfIEJbMoV/SWH+0vzHm8OZv29
QY8m68jZXMGoQL7ABDbliv6Sw/1FefXvIx3mOpEPq4MeTVaR07kC45AvMIFN
uaK/5Hh/aT8hMu0TTod58fagR5NV5HSuwDjkC0xgU67oLzneX5SyX3rHkepK
gh5N1pDzuQKjkC8wgU25or/QX8LnT+d/xukv874g0ncl6BFlBTmfKzAK+QIT
2JQr+gv9Jcy++d4czFvPBj2arIBcgUnIF5jAplzRX+gvYa5dFXnuy05/efrT
Ir89F/SIrIdcgUnIF5jAplzRX+gvLic2xpxP/fOgR2M95ApMQr7ABDbliv5C
f4njlR9451Pr/jAwbMgVmIR8gQlsyhX9hf4SR8cpZz9e7TCFf+IcV4JhQa7A
JOQLTGBTrugv9JcEdk6PWcs7J+jRWAu5ApOQLzCBTbmiv9BfEtDzp+ff6PSX
GdeLdLUEPSIrIVdgEvIFJrApV/QX+ktSGrZ6czBr/jHo0VgJuQKTkC8wgU25
or/QX1Ky9idehzn6etCjsQ5yBSYhX2ACm3JFf6G/pKS71duX95kbnH16IW3I
FZiEfIEJbMoV/YX+MiDvrfTmYF6/J+jRWAW5ApOQLzCBTbmiv9BfBuWVO70O
c7w06NFYA7kCk5AvMIFNuaK/0F8GpesD55oC2l9m/75Ib0fQI7ICcgUmIV9g
AptyRX+hv6RF9XJvDkbX9cKgkCswCfkCE9iUK/oL/SVt3GsLhKxeFvRoMh5y
BSYhX2ACm3JFf6G/pI1ek3r27zn95anrRdqPBz2ijIZcgUnIF5jAplzRX+gv
Q6Khwrm2o3aYRX/m7NULSSFXYBLyBSawKVf0F/rLkNn6a+84Uvmvgh5NxkKu
wCTkC0xgU67oL/SXIaPXpF78da/DHF4T9IgyEnIFJiFfYAKbckV/ob8MiwsN
IjM/7a2Faa0JekQZB7kCk5AvMIFNuaK/0F+GTX25txZm7ue5vkA/yBWYhHyB
CWzKFf2F/jIids/0jiOtuEPkWl/QI8oYyBWYhHyBCWzKFf2F/jJi1vyT12HK
fhn0aDIGcgUmIV9gAptyRX+hv4yYj34rUvgnXofZ+0zQI8oIyBWYhHyBCWzK
Ff2F/uILnadFnv1spMNc51y3OschV2AS8gUmsClX9Bf6i2+01XrXeZz2CZGG
rUGPKFDIFZiEfIEJbMoV/YX+4itNO0XyPul0mBnXi7z/dtAjCgxyBSYhX2AC
m3JFf6G/+M6R17zzqmf8Ts52GHIFJiFfYAKbckV/ob8YQa9PHdthTr8V9IhG
HXIFJiFfYAKbckV/ob8Yo3p5TIe5PtRh9gY9olGFXIFJyBeYwKZc0V/oL0ap
LvY6zPRPiRx7M+gRjRrkCkxCvsAENuWK/kJ/MU71CpEnP+F0GP3fg4uCHtGo
QK7AJOQLTGBTrugv9JdR4cRG5zqP0T3uKh4LekTGIVdgEvIFJrApV/QX+suo
0XJAZNYNXodZfZfI5a6gR2UMcgUmIV9gAptyRX+hv4wqFxpE5t/odZjnvixy
9mjQozICuQKTkC8wgU25or/QX0ad3g6RlX/ndRg9rnR4TdCj8h1yBSYhX2AC
m3JFf6G/BMLHH4tUPumdm6Su/3lWHU8iV2AS8gUmsClX9Bf6S6Cc2CQy8zNe
hyn4nEjTrqBH5QvkCkxCvsAENuWK/kJ/CZyuFpEVd3gdRudkyn5p/VwMuQKT
kC8wgU25or/QXzICPZ60f4Gzx120xzz7WZEja4Me2bAhV2AS8gUmsClX9Bf6
S0Zx7pjIsr+OmYsJ+dJ3Rc4eCXpkQ4ZcgUnIF5jAplzRX+gvGYleO2nW//I6
jO7b+8b9zrEmSyBXYBLyBSawKVf0F/pLxtJzQaT0371rD0SvobT11yKXzgY9
ukEhV2AS8gUmsClX9Bf6S8aj+9u9cmf8MSXtMbrGN4PnY8gVmIR8gQlsyhX9
hf5iDXpe9bLb4ntM3idFSv5N5IOqoEeXALkCk5AvMIFNuaK/0F+s41SlSPG3
4nuMqt3m8GqRvitBjzAMuQKTkC8wgU25or/QX6zl/X0ia/4xfn2Mmv8ZkbKH
RFrfC3R45ApMQr7ABDbliv5Cf7GeztPOmt78zyTOySz6msjup0UuNI76sMgV
mIR8gQlsyhX9hf6SNVy9LFLzqsiKb8dfVylq0V85XWaUrndNrsAk5AtMYFOu
6C/0l6yko0lk53SRwq8k9hh1/hdFyh8WObk51Ht6jQyBXIFJyBeYwKZc0V/o
L1lPW63ItskiC25K3mX0XOyXviOyJ1/kzH6Ra32+PC25ApOQLzCBTbmiv9Bf
cor2EyJ7n3HOVeq/7jfqjOtFXv6eM3/TuF3kyqVhPRW5ApOQLzCBTbmiv9Bf
cpbLF0WOvu7s8Tv388m7TPTaBboOWK9fcGixs9dMGudokyswCfkCE9iUK/oL
/QUi6HlM1StE1t/rrI9J1WfUaZFOU/KvIm/NEWnYKtL9YdzDkSswCfkCE9iU
K/oL/QVS8NtzIsfecM7NfvFvRZ7+9MCdJrr3jB6bevMBKZ/6HZETm0TOn/Rt
TQ1AFN63wAQ25Yr+Qn+BNPn4Y5Fzx0TeWymyZZJznnbsNbIHm6957kaRlX8n
smm8yNtzQyEvddYWX+kO+icDC+F9C0xgU67oL/QXGCF63EiPH71dIPLGfSIv
3CIyM8leegPO2/yuyJI/F1n1I2fv4LeeFTm8RuT0W85xrWtXg/4pIcPgfQtM
YFOu6C/0FzDDrKkTnWtOVhWJbH3U6SaFfyLy1PVD6zZhrxN55vdEFoU6zsrv
h49PyfbfiBwoFKkrcXqO7jH80W+D/rFhlOB9C0xgU67oL/QXMMOAubrUJvL+
285+wbonsPYR3YNG96gZVr+JUe8/93POfsOv/MBZj6z9Sc8br17uHLfS59Zz
yXsuiHx8bfReFPAN3rfABDbliv5CfwEzjChX2itaa5z1v4eWOHMtev627kuz
6E9FnrlBkl4jYVhe56w71nOutPPoc7x2t8jGB0PP+7hzLKt6mTPPc2qHyIfV
Ih2n6D4Bw/sWmMCmXNFf6C9gBuO50nOauj4Q+eAdp+dUvyiye6ZI+a9EXr9H
ZMUdTtd59rMieZ/0qesk6T66358+h16rQdf+vPRdkbU/ceaUNv+3SOWTztog
PY6ma3rqy0Sa9zjXB9djXnqel6FrOGQzvG+BCWzKFf2F/gJmyLhcXe4K9YUG
kTMHnb7z7kvOeVA6x7LxF6HO8c9O51n8lyLzvhBZg+zXHE8a6j6Beo66diE9
jqbjWP43znofHZvOP+na5orHRHbNENk3z+lEegzu2JsiDRXOcTHtRXrOunY7
3aMwS9c+Z1y+ICuwKVf0F/oLmCErcqXnjPd2OseL9LiRHj/S40g616NzKjum
OvM9usZm9V0ixd8K9Y6vO+eKz/69ka/l8ctpkW6kY9JuVvjHzjhfvN05XqZj
X/czZ85IO5Lu+aPzRrpmaP+C0M/7gnPevO7XrPNHpypDXWmf05XajzvniF06
65wLP0p9KSvyBRmHTbmiv9BfwAzkKoIe5+rtcD7jzx5x5khObnG6gK4n3v+c
s4ZZ51U2TXC60Jp/cnrFsr92zrmaf6MzL6MdJNV1qzJJHaN2N11XpOMOd6av
OufIL7vV6Xm6F5D2Jl1rpD/zhv90umDF/zi9UF8T7Yh6jlm0Px15zVl/HXr9
lk39N6dDaa88e9SZW7t4xjkep3NtaVzjAqA/Nr1v0V/oL2AGcmUQ/WzW9cMX
33f2FNQ1QHquen15pBetEDm4yLm2g16HUzuBzqvo/IquDdJz2XWdjvYjPU6l
a3f0Glg6P6MdaZqp9UJBzD190lmjpHsMzf5959w0nR/Tc/kX/4XTp/Q4nb4e
r9wZ6lQ/dl6j9T93rg2mnXLzRKdfaq/SY3d7Z4vsm++8xjoX9+7LztqmuvXO
sUk9lqe/D+1Xer0w3adR56l0Hq+rxZmr0nm9j3qy9vierdj0vkV/ob+AGciV
5ei5VXrtcZ3P0Lkj/fz98F3nM1mPo+nntHYlnRfR+RE9zqSf69qXtk1x1i7r
uiLd01D7gM616JyLzr3oNSa0O+icjM7NzPnfzl7OM34nu7pT2l7nrDHXOStd
d6Xn1+lrop1SXw/9XkHov4u+4bx2+hqG+9YPnNdV10fp8T99rUv/w9njuvxh
Z98AXd9VOc2Zzwr3rnnOnFbVUmf+T39/4e5VEvrg2SBycrNz3fnm3ZH+9Y5z
LuC5OpHz9aEO1uR1MO3Qeszw6uWsORfPpvct+gv9BcxArmDY6LojPSdL5yi6
W0P9qdnZr0fnMVoOhc/fWj71X5wOpZ+7tatCn8XFzmey9ig9513nSXY84cw9
6We5dimdf1r3L875YToHpcfoon1Kz51f9GciC77idSrtETM/7fSKaRYctwvc
65y+pa+XzuOF57x+z+ti4XmvrzjnBWp/feFm57XX66vp2nntt6/+vTMHpp0s
Og+mv7cN/+XMhUV72bbJzu9X+7Ked6jdTNfj6+//0GKnU2smwv1stdO1dZ27
ZkaP32pH0zky3ftS1/TrPFmopz039RdO1vTcQO3tug4+2tX0uKTOmen8Zwb0
NfoL/QXMQK7AJIHkS3uVfnbpnMNvzzufbTofEe5Wh53PwDP7nbmLxm3OWme9
BuqRtSI1rzjzHbqfkX7G6tqePfnO56/ub6RrpnXOSudOdA5F1wStHet89utx
L107pHs86rGu2L6lc1jaC/S4mK41CneuzzjHzML7BoziOXQ553VOr53+Kef1
nhnpbLpXuP4uCj7ndGG3t33NWc+ma+d1rwX9PervU68lp/Npeq5huL/d5XRs
XRumfTva4TQXui+VHgsOZYX+Qn8BM5ArMAn5GgI6V6DHeLR36TyC7n+ta511
PY52L11XrscGWw448xFNO501POH+9aYzd6FzXLrOR9f7aAfTY1A636HzHnps
So9R6bEqne/S9UL6GRud89LPXz2+pXMqOrein9E616JzLtE+pnMxOiejczP6
WR/uZJ/3+pseX9R+EO1lNqxjNyz9hf4CZiBXYBLyBWF0/bMea9Rupuf56Xot
nRfTYz96DCjcz4465/rrWh6dHzu91+loOkem631ObHTmyUI9bc3UH0fWdBU7
x6D0WJR2NV03pMcldc5s11PO/gI6b6brurc84hzX0uNbepxL133rWqSSf3WO
gbm97YfOmiU9bqlzLnrcTNfQ61yMzqfpHJvO0YTn1L7s7Amu82rRDqdza3pO
39POMU36C/0FzECuwCTkC0xgU67oL/QXMAO5ApOQLzCBTbmiv9BfwAzkCkxC
vsAENuWK/kJ/ATOQKzAJ+QIT2JQr+gv9BcxArsAk5AtMYFOu6C/0FzADuQKT
kC8wgU25or9MRUREREulvyAiIqJt5mp/AQAAAPuhvwAAAIBt0F8AAADANugv
AAAAYBu51l8QERERU0l/QURERNukvyAiIqJt0l8QERHRNukviIiIaJv0F0RE
RLRN+gsiIiLaJv0FERERbZP+goiIiLZJf0FERETbpL8gIiKibdJfEBER0Tbp
L4iIiGib9BdERES0TfoLIiIi2ib9BREREW2T/oKIiIi2SX9BRERE26S/ICLa
47lz52Tjxo1SVFQkCxcuRMw4NZuaUc2qyX8L9BdERDs8e/YsvQWtUbOqmTX1
74H+gohoh/o3rX4ubN26VXp6etJ6zwYYbTSbmlHNqmbW1L8H+gsioh1G517o
LpDpaEY1q0uXLjX274H+gohoh9F5+Y6ODmlra5PW1lbEjFOzqRmN5tXUvwf6
CyKiHUY/Dz788EPEjJf+goiIKv0FbZL+goiIKv0FbZL+goiIKv0FbZL+goiI
Kv0FbZL+goiIKv0FbZL+goiIKv0FbZL+goiIavTz4IMPPkDMeOkviIio0l/Q
JukviIio0l/QJukviIio0l/QJukviIio0l8c694qlYIpD8pd3/2ufFe96y65
f9J0eXnzQTmdAeNDR/oLIiKq9JcaeX7cX8mYMWNS+41HpaL+w4T7NlZXyPKl
y6X0rWMZ8HPkhvQXRERUo58HLS0tOWizvDLuc25P+cb9ebJu216pqamRA3vL
pHDyWK/D3PiI7G+Ov//mvD8Pf+8PH9uYAT9Lbkh/QURENZf7y+m3Frr95BfL
3k56m8a3XpA/it7m5Xfjvrd95g/CX//W01sC/1lyRfoLIiKqudxf6jc/FTk+
NF1ODHC7Vx4YEz/P0nxCjp6okVfG/5/w17/wYLHUnDganrc50Zz8MRpqDkj5
unWyLmRpebnsPVCT8vmaQ49VVXNUmt3/fke2he6zbec2KS/fJlUnmgN/7YKS
/oKIiGpO95ft6fWXcJ+oqpKjDU5viB43SuYfPtZvLqb5HSkc/63kt7/jESmr
Od3v+U5I/i36/VulrKFBSqb9NOl9f/Fcbs750F8QEVHN5f7SuP0Zrw8s3pH2
/WpLF8nEyRPlu26f+LFMnjZZJk6cKIvLa73bNlTKhJjOcce4KbJgyRKZOTFm
Xc2Y78rqqtgOc0IKvuP0l3Hjvh25za3y8MxCWbLgSbnrJu/xvvV07q27ob8g
IqIa/Tw4c+ZMDvquTLklZl7j5nHy3Opy2f/e8bTuv7Mguv5le9Lvb5jyf93+
sajiaNz3mt55Q34Wfd5vz5Xj7veORfqL45f+YZYcaop93GOycsrfut9fuL85
A17H0ZP+goiIam73l5ANu2XKd5Ic27npVrlvcr6sLtsrDSnuuy26fnfq5sTv
N25x+8l/r6pNev/mA89Hnu+PZJnbQ2L7ywOyuynZcx+W/Mhtvv7w+uBfw1GU
/oKIiGrO95ewTbK/YpXMnHyf3HJTki4z5seyrPJEwv0G6i8ntkXW1oyZIPtS
Pm+DFP4o2nGqI1/z+svY53alHHPNml9G1u7kyZHAX7/Rk/6CiIgq/SXR4+/t
l7J1y2TSj74Y12PmVzbG3S6t/vLtWTHHhhLdFjkG9VfuY3j9ZUZFYmeK2lK1
wjmv++uz6C8+Sn9BRLTD6OfB+++/j0l8b9M8uTXaYX5YKCdjvlfxdLS/lCfc
73jFdOc+Y5fG3ae/iY9xTOZE+ssTm46kHlvDZrkrMje05eSZwF+n0ZL+goiI
Kv1lcN95+T+cLvL1fDkc8/W0+kvoPscGeOyB+stTW0+kvF/T/sjamW8P/PjZ
Jv0FERHV3O0vx2RBZO3JUxtT9wT1yLqHknaRgfpLQ+WsyHGnnw0wP1It0yLn
P/36jaPuuKL95VtTN6Qc0/4X/81d/3J4gLFnm/QXRERUc7e/nJIX749c++gf
Cgacwyh98s7k8y8z/yZlf3n//bdlfOS4009n70z6uEdKf+Oef7TiUFPk615/
0b1hXns3Sfc5s9N97B/O2JYBr+XoSX9BREQ1d/uLzqs84q7NvXFsvmx5tyH+
Nier5eUn/9m9zb0v7I2/f1mkf3xpgmw/ltgzKhf8xL3vf80vj1sHs3/dU+51
lcb8YmXM/WL7iz72z+TVfcfd7586vF0mu9+/Vd44nDtrX1T6CyIiqtHPg9On
T+ekZTO/H3eO0ZfvuEd+8fDD8ou7fxh/DvXYBVLX776nDi2Ju83NN98svyra
G3ObOll83+dj9pS5Re644w65I3bPvBsnya7603H3mXNH5HrY/3CH99h6vzvu
iHu+X726P/DXb7SlvyAioprr/UXd98bzcs/NX0p+jaIvf0dmrNgqjSnuu+fV
p+Q7MXvG/OUT5f1u0yhl83/lzbXEeO/TL0ltwmN6/eWZ7cdk34pHE8f0pZ9J
0ZbDgb9uQUh/QURElf7iWVd7UHZv3yJbtjjuPlibsrf0t76+XuobGwe4Tb3U
1tZKXV2dVB+slrrGVLfz+stvNh53vtZYHxpbrVRXH5SD1emPKRulvyAiokp/
yTRj+sum3JxjGUj6CyIiqvSXTJP+MpD0F0REVKOfB83NzZgRHpGnb470lw3H
MmA8mSX9BRERVfpL5tlwtEaqqmqkIQPGkmnSXxARUaW/oE3SXxARUaW/oE3S
XxARUaW/oE3SXxARUaW/oE3SXxARUY1+HjQ1NSFmvPQXRERU6S9ok/QXRERU
6S9ok/QXRERU6S9ok/QXRERU6S9ok/QXRERU6S9ok/QXRERU6S9ok/QXRERU
i4qKwp8H+h586tQpxIxVM6pZXbp0qbF/D/QXREQ73LhxY/gzYf369XQYzFg1
m5pRzapm1tS/B/oLIqIdnjt3zp2DQcx0NauaWVP/HugviIj2ePbs2fDftEuW
LAn88wkxmZpNzahm1eS/BfoLIiIi2ib9BREREW2T/oKIiIi2SX9BRERE26S/
ICIiom3SXxAREdE26S+IiIhom/QXREREtE36CyIiItom/QURERFtk/6CiIiI
tkl/QURERNukvyAiIqJtDre/XL58OfCxIyIiYu6pHWSo/aWhoSF8+0uXLgU+
fkRERMw9tYNoFzl58mT4v9PhzJkz4fu0t7cHPn5ERETMPbWDaBc5ffq0XL16
Na3+0tHREb5Pc3Nz4ONHRETE3FM7SHQupa+vL63+orerr68P3+/ixYuB/wyI
iIiYO2r30A6iXaS3t1c+/vjjtPqLEp230bUwet+gfxZERETMfrVzRNfhnj17
Nu1jR1GuXbsmTU1N4fvr/9JhEBER0aTaNaLd49SpU+FzkIYy9xJFH0vX/Ubn
YTiWhIiIiCbUjhGdd9Hu0dPTE55LGS76mNEuFF3Tq8eW9Lwm9odBRETE4agd
QruEdoroWt3ovIt2l3TX7A6E9p9z5865a3oRERER/VQ7hq530V4zknmXZOga
Gu1Jei529LgSIiIi4nDULqGdQruFrn3RnjGc9S7poo+t8zr6PEHPPyEiIqK9
apfQTmGytwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
QG7z/wFt4Sws
"], {{0, 752}, {560, 0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag[
"Byte", ColorSpace -> "RGB", Interleaving -> True,
Magnification -> 0.5],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSize->Magnification[0.5],
ImageSizeRaw->{560, 752},
PlotRange->{{0, 560}, {0, 752}}]\)Rediga las probabilidades de puntos a lo largo del eje x.
Show[Table[
Plot[trained[{x, 0}, {"Probability", col}], {x, -5, 5},
PlotStyle -> col], {col, {Blue, Green, Red}}], PlotRange -> All]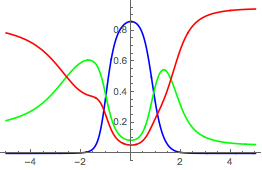
Represente gráficamente las probabilidades de cada clase como los canales rojo, verde y azul de una imagen.

row = Range[-4, 4, 0.05];
coords = Tuples[row, 2];
preds = Partition[trained[coords, None], Length[row]];
Image[Reverse@Transpose@preds]
Represente gráficamente la densidad de probabilidad como una función de posición para cada clase por separado.

GraphicsRow@
Table[ContourPlot[
trained[{x, y}, {"Probability", col}], {x, -5, 5}, {y, -5, 5},
ColorFunction -> (Blend[{White, Darker[col]}, #] &),
PlotRange -> All, ContourStyle -> None], {col, {Red, Green, Blue}}]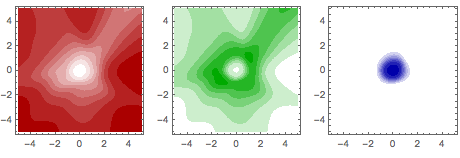
Represente gráficamente la entropía de la distribución posterior como una función de posición para visualizar donde la red es más incierta.

row = Range[-5, 5, 0.05];
coords = Tuples[row, 2];
entropy = Partition[trained[coords, "Entropy"], Length[row]];
Image[Reverse@Transpose@entropy]