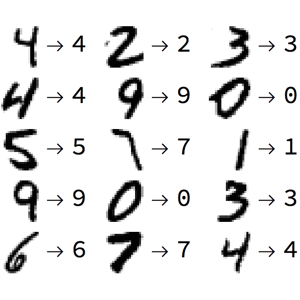Aprendizaje no supervisado con Autoencoders
Entrene una red autoencoder para reconstruir dígitos de escritura a mano después de que se proyectan a través de un "código" de espacio vectorial dimensional inferior. Utilice estos vectores para realizar agrupamientos y visualizaciones.
Primero obtenga datos de entrenamiento, y luego seleccione las imágenes correspondientes a los dígitos del 0 al 4.

resource = ResourceObject["MNIST"];
trainingData = ResourceData[resource, "TrainingData"];
trainingSubset = Select[trainingData, Last[#] <= 4 &];
testData = ResourceData[resource, "TestData"];
testSubset = Select[testData, Last[#] <= 4 &];
RandomSample[trainingSubset, 8]Obtenga la "imagen promedio" para sustraer de los datos de entrenamiento.
trainingImages = Keys[trainingSubset];
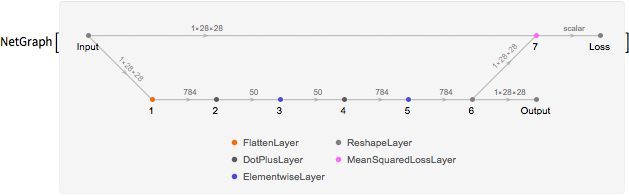
meanImage = Image[Mean@Map[ImageData, trainingImages]]Cree una red para entrenar que produzca la reconstrucción y el error de reconstrucción.

net = NetGraph[
{FlattenLayer[], 50, Ramp, 784, Tanh, ReshapeLayer[{1, 28, 28}],
MeanSquaredLossLayer[]},
{1 -> 2 -> 3 -> 4 -> 5 -> 6 -> NetPort["Output"],
6 -> NetPort[7, "Input"], NetPort["Input"] -> NetPort[7, "Target"]},
"Input" ->
NetEncoder[{"Image", {28, 28}, "Grayscale",
"MeanImage" -> meanImage}],
"Output" -> NetDecoder[{"Image", "Grayscale"}]
]
Entrene la red para minimizar el error de reconstrucción.

trained = If[$VersionNumber < 11.3, NetTrain[net, <|"Input" -> trainingImages|>, "Loss"], NetTrain[net, <|"Input" -> trainingImages|>, LossFunction -> "Loss"] ];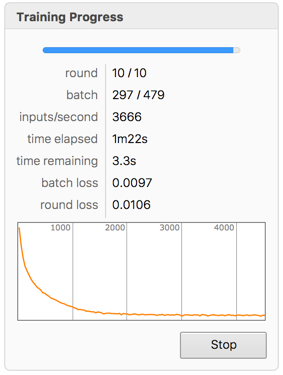
Obtenga una subred que realice sólo reconstrucciones.
reconstructor = Take[trained, {NetPort["Input"], NetPort["Output"]}]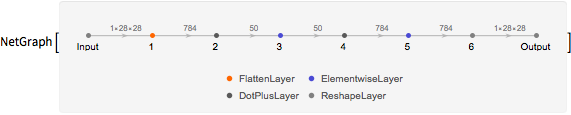
Reconstruya algunas imágenes de muestra.
ImageAdd[reconstructor[#], meanImage] & /@ {\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJxTTMoPSmNiYGAo5gASQYnljkVFiZXBAkBOaF5xZnpeaopnXklqemqRRRJI
mQwU/x9A8CWTyfQBDrlbLCxMU7BLvbLCKTfRkQUoFzbpIBY5JhaQHAuL8hkM
KU8GJiAQVQQS6FIHlED6cjYdrGdhmYYqdV8CaJxy2df//x9IsvD0/UJ3vvNr
MHMSUNUdNDmzhxDmA3N0OYQL7psyMEUjyxWzsMCYGGaqweReHQC6SvIhVrl8
oE+UDv3HJuepBJTzRvWfKhPTtm3STEzgwEGV+t8HDkoIkYMmBwwNiJyk052v
aHL/DxZC5LDH3/ZAlqAd2x9ilaMPAABwyokL
"], {{0, 28}, {28, 0}}, {0, 255},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Byte", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{28, 28},
PlotRange->{{0, 28}, {0, 28}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJxTTMoPSmNiYGAo5gASQYnljkVFiZXBAkBOaF5xZnpeaopnXklqemqRRRJI
mQwU/x9gcJNxEk65FcxrccpV8OGUusSdiVNuNeMBnHKmCl9wSd1nVMepbQGj
DU65YsZNuKSOCRl9xyXXzBCF08gQxnW4pJ6La+DU1s6YgFMug7EQp5w0415c
UodYcMsVMRr9wSH1VYOxDZe2X5b+X3E6hS4AAAjL8xI=
"], {{0, 28}, {28, 0}}, {
0, 255},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Byte", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{28, 28},
PlotRange->{{0, 28}, {0, 28}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJxTTMoPSmNiYGAo5gASQYnljkVFiZXBAkBOaF5xZnpeaopnXklqemqRRRJI
mQwU/6cp6G4KYWDIXIRNKowJDFQfYpfSKvRnYmrFkDrNyqR7//P/n4ZMxRhy
m1h0nwGpVnamfZhmPngLIvWYsMmBQRcHk+VX7FKbOZgkDuDQVs/ElI9Dyp+T
KeEzdqlnokxid3Bos2RiKsIhtZGdyQmHiW/McWurZGIKwqHtPzsT0zMcUiC5
K6+B4Nf/X69f38rMzMz5iiwHBuEFkVBWC1wukAkB2Dg4wrq6jiEM7WxpaQFp
SWlpuYbL4gEEADLRqO8=
"], {{0, 28}, {28, 0}}, {0, 255},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Byte", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{28, 28},
PlotRange->{{0, 28}, {0, 28}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJxTTMoPSmNiYGAo5gASQYnljkVFiZXBAkBOaF5xZnpeaopnXklqemqRRRJI
mQwU/x8Q8Plabu55HFJ1TExMrDFvsclVMYGB1E4scrOYmPNmThFi4qj/iiHn
xRQBJA+JMDHF/EKXY2C6AqKO2jExRf9Gk3Nhug+mTwgzMa1Ek8sFys12XLFi
RQ4TUwua3EKmjdfZIW5lUlj9AUXu4+LPd/iZYIB7Gbprt8T5wGX1rqC79s/7
9zduvn+fx8PE5IYagK+PwlhH9ZiYPJClNilxbICxP6kw8W9HklvKwcR8DMY5
xcLkgKyxm4npCIw9h5kpD8UfzkxKiTdBrAk6nEyocv8/K3EysbABAcgX5m/Q
PLHAQxriP5vmF+ge/P//+a3SrY3Lb/3AlKEHAAAeUY84
"], {{0, 28}, {28, 0}}, {
0, 255},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Byte", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{28, 28},
PlotRange->{{0, 28}, {0, 28}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJxTTMoPSmNiYGAo5gASQYnljkVFiZXBAkBOaF5xZnpeaopnXklqemqRRRJI
mQwU/x+U4Kw8lLHzEYZcmwSUkR2OLvXbBiY3X/cLmtwu5kooq5f5FarUJWG1
z1CmPbpcOMcpKOstAxOq3GpeHRiziMnpF4pcGPNUKOu+OOteFKkPcswwZiWz
DorU/5fM0QgTIlDlvhnrvYWqYmKagioHVG2xCgjqom2Y4TbDwLVQLmYgEJdg
YWb+9h8dnFsNBP//xzEzY0jBQAMz8yVccvVMTPj04ZSrYObGKScuPAGnnM9e
nFJUAQDVl858
"], {{0, 28}, {28, 0}}, {0, 255},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Byte", ColorSpace -> Automatic, Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{28, 28},
PlotRange->{{0, 28}, {0, 28}}]\)}Obtenga una subred que produzca el vector de código.
encoder = Take[trained, {NetPort["Input"], 4}]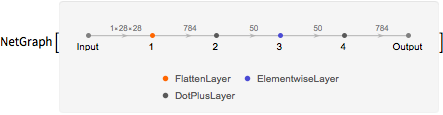
Calcule los códigos para todas las imágenes de prueba.
testImages = Keys[testSubset];
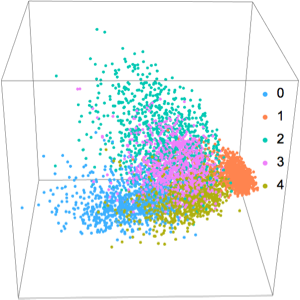
features = encoder[testImages];Proyecte los vectores de código en tres dimensiones y visualícelos junto con las clases originales (no vistas por la red). Las clases de dígitos tienen a agruparse.

coords = DimensionReduce[features, 3];
classes = Values[testSubset];
Table[Extract[coords, Position[classes, i]], {i, 0, 4}]
ListPointPlot3D[
Table[Extract[coords, Position[classes, i]], {i, 0, 4}],
PlotLegends -> PointLegend[96, Range[0, 4]], BoxRatios -> 1,
Axes -> None, Boxed -> True,
PlotStyle -> Map[ColorData[96], Range[1, 5]], AspectRatio -> 1]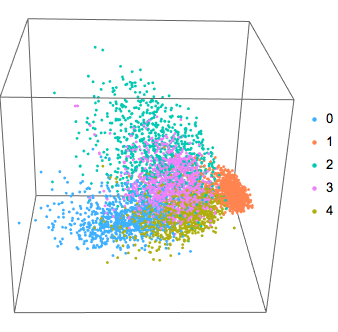
Realice agrupamiento automático directamente en vectores de código y muestre una muestra tomada de cada grupo.
components = ClusteringComponents[features, 5, 1];
Map[Part[testImages, RandomSample[#, 10]] &,
PositionIndex[components]]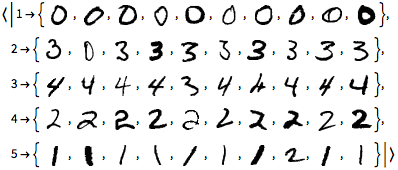
Visualice un agrupamiento jerárquico de representantes aleatorios de cada clase.
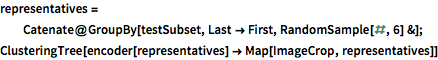
representatives =
Catenate@GroupBy[testSubset, Last -> First, RandomSample[#, 6] &];
ClusteringTree[
encoder[representatives] -> Map[ImageCrop, representatives]]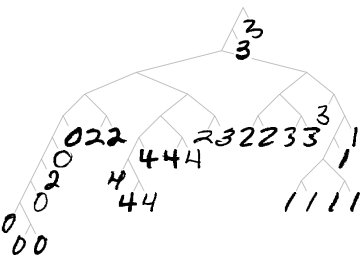
\!\(\*
GraphicsBox[RasterBox[CompressedData["
1:eJztnQd0FFX7xjG0QEgIoYYekCpIByXSwUIAURBE/BApKh8ofoJ8gAWkg1Gk
KU0FBYVEhL8ISpEaCEElIZAIKYROiIQYahKE/T/fvod7xtnd2ZnZNrt5f+fA
2Uy5e3fm3uc+t4cNG/vssKJFihTxe6BIkdfw73+fTQzDMAzDMAzDMF7InTt3
xo4d6+fnV7ly5ffff3/ZsmU4ojWQlStXDhs2rEOHDqNGjbpy5Yor4skwjHHY
s2eP3z9B9r9165b6ED7//PMSJUo8cJ/Q0ND58+fn5+e7Ls4Mw3iWt99+G1pR
rFix8uXLBwcHk3TUrl07MTFRpfHo1q3bAxbgoKtjzjCMpxgwYACEokGDBvic
lZUFs+Hv70/qsW/fPjUhFC9enLQiMDAwICCAPuP2kSNHFhQUuDj6DMN4gCFD
hgjdILZs2dKmTRscDAsLS05OthsC6UapUqUWLFhw6tSpJUuWlCtXjtTj448/
ZulgGN9jxYoVkIg6depcu3ZNHLxw4ULbtm1xvFevXnZbKkg3wsPD//77bzqS
lJRUt25dko6oqCgXxp5hGE+wfv16qpU8//zz0uOQDogJjk+ePFnZM4SGhpJE
SFtTY2NjQ0JCcLBVq1auijrDMB7i6tWrpBtNmzaVnZo1axadioyMVAjhlVde
Id04fPiw9Pi0adOKmlG+nWEYrwPVkCeeeALiULZs2ejoaOmpS5cutW/fHqdq
1aoFebEVgtCN/v37y061bNkSx3v27OmSqDMM4zl27dpFvgLSERcXJz21c+fO
0qVLK1sO2Ax/f3/oQ9u2bWWnxo8fj+NhYWGnT592SdQZhvEQt2/fJssBtmzZ
Ijtbv359HB89erRCCE2aNIE+BAQEbN68WXp8//79xYoVw6nZs2c7P94Mw3gU
YTl69Ojx559/Sk9RK0fv3r0Vbsc1VFVp3bq17FSbNm1wXFl2GIbxRmA53njj
DZKOxYsXS0917NiRjivcfvPmzX79+kEfihYtum7dOukp0o0XX3zRJfFmGMaj
HDt2jPShc+fO0uNUT8H/yrf/9ttvNJCjfPnyubm5dPDu3btwIFxPYRhfJS8v
7/HHH4dENGrUKDMzkw4iv5csWRIHly5dajeEnj17Um3l2WefpSPQIjrSrFkz
VIVcGHuGYTyEaOUIDQ0dMmRIWFgYicagQYPEWFAF/v3vf5NKlChR4rXXXjt4
8ODChQvFTLdly5a54ScwDONmCgoKunfvLptWP3jw4DNnzqi5fcyYMdIpsaiw
0Pz68PDwVq1aScexMwzjS0RERJBc1KlT580331y+fLkap0EcPnzYckI9Dd5I
S0tzabQZhvEgKSkpyOnQjZkzZ2q9Ny8vr3PnzlLRePLJJxGgK+LJMIyhWLhw
Yf369RMSEnTci5pOXFzc66+/jhA6derEw0QZptBy7969Gzdu3L1719YFd+7c
UV+dYRimkJCUlHT27Fmrp27evHngwAHWDYbxMVDpqFy5Ms1qX7Ro0V9//aU1
BBIHq5bjjz/+sCUpDMN4KcnJyVWqVCl6Hz8/P9nsM5VYtRxsNhjG96Blu0gx
pk+fPmLECOhG165dVQ7JkGLVcrDZYBjfIyUlRYzg+umnn3Dkf3vI+vmFhITs
3btXa2gyy8Fmg2F8EugGmY1evXrRkT179kA0cGTgwIFaQ5NZDjYbDOOTWOoG
WL16NR0cOXIkpEBTgMJysNlgGF/lxo0bffv2hUR07dpVSERWVlbPnj2pjVTr
CHBhOZKTk3U0kjAM4xWIHWCpfYPIycnp3LlzkSJF5syZozVAWI7U1FQ2Gwzj
w9y7d49qJT///LP0eHR0NMTE8rhdYDm2bt3KY8gZxoeBbjRp0gT6MH/+fNmp
999/H8cfe+wxTQFCNw4ePKgw7JxhGB9g4cKF0IegoKAvvvhCejwjI6N69ep1
69bVNIKUWzYYpjCQkJBQqVIlq8sL16tXz3JNUQW4G4VhCg9bt26lVg5IhNRd
iONjx45VEw6P2WCYwoPQB9plft++fXT88OHDNOVNjW6w2WCYQoVUN6itA+ox
Z86ctLS0Ll26qNQNNhsMU6jIyMigXhXSDamGEC1atFAOgc0GwxRCPv30U4iD
VCuaN28Om0ETZvFZ+XY2GwxTOMnKynrooYeEboSEhDRs2BB1Frv1FDYbDFOY
QYUlMjKyfv36EA2p91i4cKHCXWw2GIYxmQVk3bp1U6ZMmTt37qFDhxSuZLPB
MIwlFy5cEJtBW8Jmg2EYS/7888/ffvvN6ik1ZuP06dPjxo17yMzs2bP37NmT
n5/vmph6E40bN8YDefrpp/EA9YUQFxeHQBYvXuzciDG6uXr1aqNGjTZu3Kg7
hOnTp2/YsMGROOTk5HTs2JGy29SpU3VUBO7cuTN69OgmTZocPnzYkZiAX3/9
9cqVK5bH7ZqNEydOhIWF+fv7h5opVqyYn59f+/btt27d6mCUvJ0HHniAxvb/
+9//1hdCkfs4N2KMbi5evIgXWq9ePWQ9fSFUrFhR3yqdAiiPdAdn/Kk1hClT
plCr5scff6w7GoRVy6HGbAwYMKB06dKff/45/fnNN9/gc7ly5QICAsaPH3/9
+nUHI+a90FKuoEqVKvpCwPtl3TAUpBtg/fr1+kLo06cPbkdxrzsOUt3o1q3b
ihUrtIYQHh5OujFq1Cjd0RBYWg67ZuPatWs1a9a0VK3ExMShQ4fidyGG8fHx
jsfNGxF+g3XDZxC68fLLL+sLAXVP3F6iRAlR1Gpl4cKFJUuWpGjoC0TITo0a
NfTFQYrMcqgxG9AZ2Upigry8vOHDh+NsZGSkQqOrDwO5cFA3du/ezbphKIRu
NGzYUOvavAQy1JNPPkl1ed2VncaNG1M0+vXrpyOQYcOGkd8ICgrStxO0DKnl
UNONoqAb4NatW126dMEFq1evdjxuBuTSpUuPSpg/f/63334rlmwdO3asg7oB
aDlHGA/nxJhxDGjFs88+66DliIqKQtUeIWhdak/w1FNPCc8AA5OTk6Pp9oMH
D4qZJrp/hRRhOVSO2VDWDZN5STFcEBER4XjcDMjp06f9LChbtmwVM5Q2QLFi
xVBrm3Wf6Oho9V9BVRX1C6QwriYjI4Nea/ny5Y8cOaIvkL59+yKEjh076rs9
MzMTSUIkueeee07T7deuXYNRId1o1KiR1Q4RrZDlULmoF+kGilr8EKsXoLbS
qVOnZs2aZWdnOx43o2FVNwSifUNG7dq1ZeGQOEwxQwaD6GyGqyqGAkWqyLO6
2yhWrVrlZx6tjaqovhBQ969cuTJFw9/fH7UDTbfjV1StWpWS6PDhw/XFQQos
x6FDh1QOECXdAJaLlwq2bt2KC3S0+hoffboRGhoqC0e0fyqgO4ExTmfSpEn0
KkNCQvQ1+6MK36BBA4TQvHnzy5cv64sGEpJIVCNHjtR6+4svvkjaBcuhY695
SyAa6enpaq6EbiBJI4P07NnT1jV79+7FBQrC4r1ANx64T4sWLdIlbNiwgeYa
iwuQTsaagaOThSN0QyoO+EwOhE5xE4dxuHHjxpAhQyjD6m4fGDRoEIWgUM1X
5vbt2wsWLKARU8WLF4+MjNR0+8mTJ/3uz1A7d+6cvjhIURg+asmnn36KONer
V+/ixYtWL0B9JywsTMe2ksYHXjE8PJzePiprlhfgVdLZli1bospmKxzRb2LV
VIhajPMizjjKsWPH6M2WK1du06ZNOkLYv38/7kUIlSpV0t2xAkqVKkUxqVat
mtZ7oV2kG6+99pruCEixNXzUKtS6O23aNKs/Pz8//5FHHvFJ3QC///57YGCg
n7mVbOfOnbKzOCKcpPLkQeV+E66qGA1YzQ4dOohCQWuPBrF9+3YKYcaMGbpj
Qr26pGBax42/9dZbIn2qtwoKaLIcixYtoq9OTU21PLtv3z6ccpagGZCmTZvS
z3/hhRdkp5KTk2m9Aru6YbWqIjvLlsNQ3Lx5U0iHvpEG58+fj4iIwO1lypTR
PY7ixx9/FJZj9OjRBQUF6u+FUxIraaDc1xcBGeotR1ZWFrUw//DDD5bRJt3w
4VGjqKnRW0N9DY9CdlaoirJumO6bCqtdrjwAzJi8/fbb9HLLli373Xff6Qgh
JiaGQtiyZYvuaPTr10/Yhs8++0z9jZA+6pAFAQEB33//ve44CDRZjtjYWLLr
CxYskJ0aM2YMPHxKSorjUTImaWlp/v7+9NYs28ZF0rKrG8pdrnRq5cqVzok0
4wxu3boFI03vFxlQRwh//fXXm2++Sa0TUVFR+qIBWyt0Q+tYKekYsPDwcH0R
kKGplYMWL61evfrx48elx5966ilfHfclQA3Xlm6sWLFCpW6YFNsxqKrCumE0
Tpw4Qf2hqGvom+yG0vnhhx9GCMgp+nZChHzp1o2MjIyqVaviRqSu9u3b6/h2
S9RbDtgt+ByKOR4jBJCOX716FXnK53Vj48aNqGOinrJ9+3bZKaEbixYtshsO
iYOCbjirRGCcCOw9veLSpUufOnVKRwgoDkJCQqA8cKeaGiiIu3fvfv7558HB
wTp0A2zevLlEiRJ+5j7ZHTt2aL3dKiotBw3uElSoUAHVky+//PKJJ56AjKgp
ar0dOI1du3ZZHhe6YdlqagnrhjeSn5/funVrestr1qzREUJ2dnb//v1xe506
dW7cuKEvGl27dtWnG6Bdu3akG87q91RpOZKSkt544w3qj/aTDJWsVKmS42sK
eTXbtm2DD1GpGyazPtg6Bd145JFHnBYzxnkkJCQ888wzfuYJ8vpWA4NTpXSi
u7eddOPJJ5/UcS8sB+kGMqy+b7dEfSsHpHLGjBmTJ0/u1KkT/kflRd9cYx8D
JgFCCgFxMJzOnTv75DQf3wBFZ8WKFfGidYcwYsQIFA26h3xHR0fj9v3799+7
d0/hMltnR44c6efU+SB2LcffZpz1dT4JXtadO3cUXiiqqMoXMF4B3uCtW7eU
r8G7dl0EEPjvv/+ucMGFCxdc9+0yFCwHFAPxvH37ttsi46WcO3fu9OnTts6e
PHlS9/wmxjjk5eXBZtsaNw676JR1cpRBKY+y3uop5NYDBw64rRagYDmQFxTm
8OIULd1D0+7Gjx9vaxqLFzF79mzY0ZdeeknT9hAFBQVIUVZnqVy7di02Ntal
xRDjNlAEZGRkWD2FEtZWjnYiUCfLuZMEUqzWGfcOYtVyQL6QFxSM2dChQ2Ub
WAcEBHz11VfeOwzs/PnzdevWhW7Uq1dPq+U7deqU1R+emJjoTvfIuBR4b6uW
QyE7Ox2rlsPNZoOwajmUzQZAoSzTDfocHh4uNWyQ6OjoaFuL/xgKRPLVV1+F
btSqVQsCqOleq5aDzYbvYdVywGxYTkNwEVY1yv1mg5BZDpIv5VagqKgo0S07
ZcqUXr16iS7aoKAgk7kDqF27duXKlcNxyzHqxmTAgAG0pIblBFi7WFoONhu+
h6XlcKfZIGSWwyNmg5BZDrtmg6AB/DK/Yfl5+fLlroy7M0HB4e/vD92YM2eO
1ntlloPNhq8isxzuNBuETKk8ZTYIYTnUmA3BmDFjKlasaEs3UGfRPaPHpeTk
5IwYMcLq0gpTp06FblSvXl2hi8QWUsvBZsNXkVoO95sNQlgOD5oNQlgOlWZD
sGfPngFmLHVj7ty5LouvQ2zcuBHiMHHiRMvRVqtWrQoICMDZsWPHau2DFpYD
ZuPgwYNsNnwVYTncbzYIoVdnzpwRU8Y8BWKCh6DebMg4ex/R1tGiRQvkIKfH
03GQwakdo0uXLrJTqampLVu2pLOy+b9qIMvBZsO3IcuBzOLBqRYo5S9fvuxZ
s0HAcuzatcspdSXhPYy5GhicQL9+/aAM/v7+gwcPPmRm3LhxULwKFSqIBYc7
deqkNWFAkXbv3o1ExWbDt4HlwIv2iNkgYDmQWz1uNghkE6cMXxk5cqSoszge
miuYMGHCAyqoWrWq1grs0aNH9c25ZryIq1evoirqwd3Vb9y4ERsba5BpTZqW
AlPgypUrNWvWNLJupKen9+/fX6YSZcuW7d69u6inEKGhoZb7a9uCu1EKD7m5
uagmQEDc/9V//fUXvtope6M4C01LgcmQag61lALD9sMuXbq0Vq1aQh9atWpF
E6VzcnL69u0rlY4qVaooTykScMtGocIj0mFA0TDptRw//vijbBnDxYsXk9+A
8XBqBJ3GzZs327ZtS8rw4IMPSrtlpbpRu3Ztf3//Pn362N0Lg81GIcTN0mFM
0SC0Wg5cjBIZujFz5kxxUCyLaljdMJlXZSFxqFy5srRBOC0trVGjRsKHjB8/
Hh+2bt2qHBqbjcKJ26TDyKJh0m45oqKiaMxG//79xUGv0A14DDgNGuglWzn2
3XffDQ4OxqnOnTv/8MMPJUuWxC9SCIrNRmHGDdJhcNEgNFmO+Pj4oKAgZLGw
sDAxmx65jNo3atSo4bJoOoHhw4cj5uXKlbNswRg8eDBZjqlTpwYEBHTo0EEh
HDYbhRyXSodXiIZJu+VYvnw5jdno06fPuXPn7ty507t3b/Ib6jsjPMKqVaug
DMWLF7eshty6dQtKiLOBgYH4X0E32GwwJpdJh7eIBqG1lUM6zlyIBjh58qTr
Iukgly5doolsjRo1ys/Pl53dsGED4o+zRYoUwf8Kg3zYbDCE06XDu0TDpN1y
zJ49W4zZEBpi8J1P4RCGDBkSERExceJEy4GyBQUFtJIPaN26ta1959lsMFKc
KB1eJxqEVsuRk5MzderUZs2aPfzww927d1+/fr3dvkuPgxgqrL381VdfLVq0
qF27dpb7LgnYbDAynCIdXioaJhWWA0Wwzy94jvqLgvqx2WCs4qB0eK9oEAqW
A/V9laMovZrr168rTIrXZDbOnz+/cuXKd955Z9asWY5bFCh2XFzcnDlzEKAj
4dy4cWPhwoWO7wLDyNAtHbZEY+bMmXjXmhbN9hQKluPw4cPK02pwdsuWLR/8
Ezh/FNCWjZBG5vjx48jylse1mo2PP/5YNP7861//cjBWSD9OmTy4Y8cOasPB
b3EwSowMHdJhSzTmzp1LKSc0NBTZyqnRdAlWLYddszF58uQKFSqIjWU7dOjQ
qFEj2h0b/1etWjU6OtqVsXYmtiyHJrMB+S1btizpxoMPPqh7EpDA6brx/fff
OxglxhJN0qFQPaGdmul1d+rUycmxdAFWLQfERMFsrFmzhjbCrly58ubNm5OT
k/EoLl26hA99+/alU8hE69evd3HcnYal5dBqNlAREJ1NLVq0cDxK77//vpBl
R8Ih3cBLSU9PdzxWjCUqpUO5TeOPP/545plnKAkFBga++uqrLoipk5FZDrtm
o3HjxiQaSJNWQ3v00UdxQXBw8Lp165wfXRdgaTm0dqNANyiPw3E1b97c8Si9
9dZbTvQbcIOOR4mxhV3pyMnJiYmJUW4Iffrpp0VJ0aVLl02bNrkgps5EZjmU
zcbFixcDAgLw03788UeFaxYsWADZbNKkiUdWMNCB1HLo6EZxut944YUX7OoG
njNMnXI8f/75Z1pmxHtb770CBemAaOCU1YWypezZs4equgT+dE1MnYmwHHbN
xqxZs0gST5w4oRzm7t27u3XrBu+BD06MqouQWg41ZuPUqVOJZo4ePYr/ly1b
5lzdkA7QtXVNtWrVHjCvsWx56pdffpk7dy6sb+3atal9Y/LkyY7HilHAqnSo
FA1COhIbn6Ojox1vKHMpwnIomw3QuXNnlboB4uLicGWvXr1u3LjhtLi6DLIc
dpcrz8/PRyXC6g4R9CdKjSeffPKbb77Zvn277lLjgfsbXbVu3drWNWPGjCFN
iIiI+NnMyJEjYXeLFy9O22ahLtmmTRu6RsduU4xWZNKhSTQA3pGwHHiDrVq1
OnTokMsi6xygGGlpaXbHbKj3Gybz7orvvfceLkY+clI0XQhZDvgHZbOxbt06
mVAo/FmiRIkWZubPny/beeHmzZtTpkyRThhcs2bN+PHj4SJk4eC41f3QYQ6h
DLLlEGvVqtWjR49FixahIgkNLCgogMTVr1/f54fwGQQhHVpFg4DslylTRiSA
tm3b6tuAwG3AEW3dutVuc8TMmTMpfapcGj05OblIkSK0O6TxgWzC4d+7d0/h
GlRJ/CRQ17OaP2UtQihcSpUqpWZTPFps7bPPPrOMTMOGDfEuhg8fPtPMtm3b
LNsxKlWqVKdOHe8aVOPVQK737t0Lq6mjTSkjI6NBgwYi5YSFhRl56iihZsaK
Jr9BDBkyBO7L4di5A+Xho8Ty5ctFjr58+TIdRJ6V5vfy5cuHhobiV1PZAQIC
Aj744ANZUDVr1lSpG/jfakP0ihUroBvKG1JAN3CNVwxE9BlQ/urefgX2UpoA
kH2cGzeno2aSrNCNL7/8Uk2YeICPPPIIfr5XjIIz2R4+KrCqGygUUGUQr5sm
yiEoPM+vzMTExMjCwS20MbcwJAqfUXlBTccyMlRVUR6ewbrhEXRv93bs2DGp
bjRr1szpcXM6di0HPFhgYCB+VJs2bezuxnLkyJEqVarQaNKFCxc6Naauwq7l
QM3LUjek/bBCNxRYu3btwIEDaYwcroct6du370cffSRMKWp2FKDdza2o5XPD
hg22LmDd8Ai6LUdeXt63334rdCM4ONj4fbJqLAe15oEePXooKCpOde/eHel/
9+7db775phe15ytbjuzsbEvdgJw2bNhQvW5ERUWtWrUqJCSErm/ZsqVs00xU
csW3KAf17LPPQhbCw8NtaR3rhqfQbTni4+PF8FGv0A2TCsuxceNGf39/ko7H
H3/c6pPBQagKLujduzf+nDRpkqui6wKULQd0Q9QgpCsXffbZZ6I5C3lZzReJ
9g3LySNCN1544QXlQL755htqqba1IADrhqdwpJVDDB8tW7bsuHHjnBsxV6DG
cnzyySelS5em39W8efNly5ZJO3C/+OILHMQpVE8gIElJSV9//bWLY+1kFCyH
1G9MmDBBegteMelAnTp1xBrOtti8eXPx4sVJZywnq7711lv0eC13x5aRmZlp
VzdKlSqFy5TDYVyBbsvRuXNnkcxUFkMeR03HCqSDiksCVXX8Opgr/E+Sgjr7
ypUrTeYM5ZZYOxMFy2FLN8CwYcNEtTQxMdHut7z44ot0veVMHzE/xW5XFOSi
ffv20A2rY2/S0tICAgJ4foqn0G05UKyg7il0w+oAHqOhcvVRFKkzZsyoVq1a
aGiorBegcuXKcB1uiKrrsGU5pLoxcOBA6amoqCg/LYuvoopB169evVp2at68
eRSOmizfrVs3PHl8u+UpntfmcXRbDhQrIqV5RROHSePqoyidF5kJDAwMCgqa
NWuWt0xnU8CW5ZDqhmWjpdCNOXPmqPkWP/NGeLJGUZPGzbs3bNgAAbc6XG3S
pEnQDfhANZFhXIEjlgMVTO/SDTWW49593BMl92PVckBJaHUmMHr0aNnZS5cu
oYZy6NChgoICNV9x9uzZmzdvWj313HPPNWjQYM2aNTpiLkDVqXz58ty44Vl0
Ww5akgLs3bvX6bFyEXYtB1Kjb8/OtjuWw9XKqSZ835Zu30CN5cjLy/ON96hs
OdQMyfYB7I7lcPVMZzxnhXl2t2/fhmPxjfTm2yhbjrS0NK0z4IyMguVAhjp3
7pytG+Pi4h6UMGjQIDeP+9q4ceO8efPS09PhiGQTUTWhII/5+fkxMTGuni8G
TUCtx5avS0hIQM3Idd+O1L7nPhkZGTpC+Omnn0aNGoU0ULdu3SeeeOJdM8eO
HVOedIyn2rt3b5F+pk6dunbtWt2PGk+PIgAmTZr0yy+/qK813LlzB7Ft06ZN
3fuMGDHi6NGjWpeGULAcqKgeOHBA5YRlxBxxQIbS9O1uxpblUDYbeLCoU0sb
D1FBCwoKatiw4TvvvJOcnKz8pZ988snSpUuRJfG+VMYTL0VEBi/01VdfrVOn
jugjbtWqlSPrJNuyHBCl1NRU3cGqB/XB+Ph4y+PIDpAUF5mN7777rmvXrjQS
nrrJAgICqlWrBkFWP6UR77pMmTI0RoUCEf9XqlSptRmr6QFvsKgFDz/8cPPm
zWfPno20YatRyCq1atXy+yf4ITNnzrR748mTJ5955hk/a9SuXXvhwoV2p1pI
sWU5/vjjD/Wj8vBGipgx+G6JVi2HgtnA8SpVqsjeuJ9kdufQoUPhymy99/r1
64sr/f39+/fvjyyvvAQByi8o0q5du+hPpAfLt1yxYkVNr1iKVZF0j9kgbFkO
15mNxYsX4yXiuRUvXhxvpF69evhfrGAPKWjfvv2RI0fsGjkUE+Lt4/+HHnpI
fBb/Q0AsR54MGzbMUjekyalPnz7ijdsFTunUqVMrVqyAhxFJAgXZt99+q6y6
I0eOFNdDsmrUqNGiRQtpumrQoAEyiMpoWLUcmsyGyTwezCt0w9JyKJuNDRs2
iKfapEkTSirSZSjoM96I1dvDwsLElWI0CEqH5cuXW70e/pnGpopxldKZpFI6
duxoVe3x6+y27lpaDreZDcLSciiYDRxcvXq1puilpKTAvYvOPjgNPLGaNWtK
N2xCiYBg33jjDZT79Eih6qdPn1YIFt7v2WefpTcO6T5z5gxy2ddff42DfhLv
YTl376OPPpIKxcCBA8UgKCE48D9z586FL1L/M8GqVat69uwpUgV+tcLFpBv4
dlwGkcSPzcvLw+fRo0fT3CJQunRp/C6V325pOTSZDZN5+U2v0A2TheVQbtmI
jIwU7xe+QhyfNm0a6g4y72HZu4Q3JdaskF5JRcz48ePxnM+Z+fDDD/Gnn8U4
K9nKOVImTJgg3tqYMWNoJa6yZctadqfKkEmlO80GYWk5FMwGHBoyIxL2li1b
UBO3GzhyN0pS3ILSk440a9YMf9qaGoNnOH/+fBrcjoo/inKFwFENgaMQfkPl
Ni5wmM8995x4+0g8kHdkT7wFeIZevXoJGUFqWbRokZowBbm5uREREaJISkpK
snVlVFQU5Bpv3/IUlFbUhdu2bavyq2WWQ6vZILxFN6SWA2lMuRtFqhubN2+W
nkKRjaeNxCMuQNq21GqET4PzZbqh8BmpSFR8Ro0aZUs3AKRmyZIltJWDACUX
ajfKbSBSy+Fms0FILYdyywaeAGVqSCLEdsGCBRcvXhRTd2XguaH8xcXwA0KX
XnnlFenzQcbHNbKWzO3bt9NZ+D2UwgoxR+KhuXX0qFVKR3Z2NmyJeNFINlLL
h7N4X7XNoNKkJkDZr/7qq68o/jNmzNB6OyFSUa1atdTfJbUcWs0GUeQ+Wm90
P8JyQJyVf6lUN1BH/vnnn2UXoLKJlCZy/dtvv20ZCL4L6oESZ8CAAUgVyroB
0ZCOpkMpTK15msAtCEfhdwnLUVBQ4GazQUgtB1yEQssGijA/s//H8xkxYsTE
iRNLlixZv379L7/8Ulq04bfs2LGDlu/A9dIlcPFjH330UZiQRx55ZNKkSVZN
C4JC5RE3InCrO+lI0ec6UDV46qmnxLtG/QgaqOZGNUBI6dXjZ2q9F4+OfhGF
MHjwYPX3Csuhz2yYvEo3yHLYNRsm84Yd0vwIR2FZGYF0iHYPOEblr8bjhVK9
9dZbtO6i3/31r94ys2nTJssm1pycnI4dOyI9K2tFsWLFoGyosH/88cdqes/J
cqDy5X6zQZDlUNONsmvXLkhuqVKlpEsWoyZes2ZNOJDhw4f369evVatWdBzP
wXJVJdQEZW0X+DP1PpTaadIuQoBnthwqL0Of64B07N+/H1mbpCMsLOzbb79V
c6NdIP76dGPt2rXPP/883Ytakt2FDiwhywHlUd8wIkU0jeq41/38akaNrYKn
LfpPLKWDriHnYOlJrAKf3LRpU7rrtddes1vif/rpp9WrV7clGkjDWrcUQSkc
Y8ZTa/yS5UBppbIb5ciRI0jVqIA8YBsop91VhkzmfcYfe+wx0S0LG9CjR4+g
oCD6U30LA1U96L2/++67KrtT9+3b16xZM3w7JSfcqHvbSlgjlCmPP/44sjyl
BPWz1PH8kQXq1atHNz744IP69gaC5UD5q89smMwLZ3mRbqCwQ3VAzWiBhIQE
agJVaMegazTphsm8Bjh1uOCu9957z+71KDSRwpHg4U+kooE/Va7HLgPZR/3o
BVeAXwQR1jRmA1YK0YbDh06i9tHIDDWEgsWLF6scF/fLL790794dtyDFSpUH
D1P9mtvUwyJ6UmB77I7nEaxcuRJZlWwqvlTfZDFRuSBQElkdG2MViJX0XkeG
osXGxuqWPu/SDZOWSbJJSUlS3fD7Z/WZGDt2rFbdMJknCdJdsjnsyuAdff31
1+KNw2Crv1dKQUEBHoK+kZOOA3OLckrTkCdboFrx+eef025uSP8qpQNiu2bN
GkixtLv8xRdftNrjoIDUdUA6NP0isfgAgGvV+tVCN8qXL480qWnY57Rp02Su
VfeEQUeWAhO64RU7IZpUr8thMjs6VJnFO8JvRErDY5deA/eiPJbDFqKObHdN
LSl5eXldunSh+FSoUMHW6lh28ZR0OFE0BNnZ2b169cLzbNKkiabiD9kNTyAi
IoKWZEce/OmnnzTd/s477wjXgXqHpmjDdUj7WVatWqX+3pkzZ9K2NdBMTV9q
MteUpaKBCosj8zp1T5I1eU9XrEDTuhxbt26V9oCgKi2tCMNv0/GGDRtqioNY
C2v8+PGabuzTp4946ciDmu6V4n7pcIVoEKhif/HFF7Sgug4tPX/+fLNmzfA8
/f39re4MpYDUdWgazYtqEcqg4OBgSgZBQUHR0dEq624oPtq2bYsvbdeuXUxM
jCa7glqJVDdQcs2YMUP3VoyOWA6v0w31lsNkLlbGjRsn2jGI+vXrQyj27dsn
6iky3UCqWL169dy5c21tOukU3Zg+fbqme2W4UzocEY27d+9OnjwZEo0IK7TC
/fe//0W5bzcTIbRsM9I+tdTUVORBP3NftqaUjOTRuHFjch06dgJF3apr164i
XamfgoS3NmnSpNGjR6OmNnXqVPVqCWnKl9CoUSPEHPKFp6HPvuq2HF7UFSvQ
ZDlM5loh9d1LvQdSmtATmW4MGDCArkQRFh4e/vLLL0ebSUhIoA+0gypYunSp
rS9NTEwcYyYpKUmYSaluOL5jr3ukw0GnkZKSgseFJ1mjRo1WrVr17Nlz8ODB
yCzLly//8ccfoc9nzpyJjIykFUrt6gaKDGoX7dGjB4ISBgNB4U3h1GOPPSa7
BQXN72asNkQnJyf73Z+lYjkyDT8c1dvevXtv2bJFOvZYgDcLwRGuQ1OFBezf
vx/fLqs+q2ft2rWLFy9GfXzo0KGIBsRZazOpbsvhdU0cJo2Wg0CWp+3Milob
wSXTjeeee060iohsjjRJvX5+9+c1NGjQwOqgCyj/nj17pGsmN23aFJllwYIF
0m5ZletxKeNq6XBW9WTnzp0waW3atAkJCVHok7WrG7m5uTS4VGrXpX/WrVtX
dsuyZcuUx2zQXBW8a8tcj7cmbceABp41I70mMzNTSEe5cuVQNbYac6szI1C4
IFGVLl1aYdcqu+ChiZ8PC601XemzHEI3vKiqYtJuOUxmjzd79mw1umEybx4h
9iSyqjYPP/ywbBC7AC/u1Vdf9VPkP//5j7NWHHKddLiiTQNl4vv3GTZs2BNP
PAG7DoOH6iS+S+VwAihwx44dxUYYQjdCQ0MtHSCypBgpiv87der0ySefSFsz
aMo8zlqOPVu/fn1Ra6DmBTkSl8EyiVNWLShCrlq1KooP5DLZ/qTz5s3DV3fr
1s3qLz1x4gSk4Kn7bNu2bZcFUCpp0lKzjr0UfZbDS3VDh+UwmZuVIB3S+Sm2
dMNkbuVA9bNixYriSlwGO42qR1RUlMLEOpO55ouk1aFDB1u64dz1Nl0hHa5r
CJUCodCtnz/88MOgQYPKlClDugEzY2tIDB4OdEa6/katWrX+9a9/zZgxA//j
FfuZZ8vCTshuRFmDmgjeuBgvKhJDyZIlQ+4Dm6GsGx9++KGYvkr3otwZb4aW
4relG9J59CrZuHGj1iep0nJIVd1LdcOky3IQyF/I/oGBgZQA8EGhmQLqgeyD
khFlouXmRMog0/3f//0f6t3S11q7dm0Ul7o7YW3hXOlwj2iYzB77yJEjjqz8
A6346KOPgoODUaAr94nAIaBCIfUe0v+V20WPHz++f//+du3a0TZ2fhLzKQVV
IVgUqyGsW7cOqc5WZlfwG9IFoJSpVq0aBEpH0lJpOU6fPi3elLeswmGJPssh
gOvzUzc/xRZ4hlBgu2ke3gPZ8L/30TdMVA3Okg63iQYBX628ZJ8akpKSVC7U
j8T/zjvvSNffgBWZP3++yjo+iqpPP/10yZIl+J+6UwVQFVuiQSAloBiaMGHC
66+/XrlyZWrgBdAThchfu3aNupCmT58uUtHgwYOl42aDgoIiIyNzc3PV/ASr
2LUcSOoxMTHCHO7evZukw4u2XRYoWw6V+doRUFtRHq3kiA/XgePS4WbRMJnz
BYycwmvCA9Q3jUIldtOJGxISfqNyzdfVCcmu5YDeuq7IczPKluPs2bPKK7o4
DjwhRNjWGGky4W5ecd0R6XC/aBAKlgO5FUWh1jV4tZKZmakwSwVFg3Kmdpy8
vDwkJFtdIcjUWls7daBgOchsKK+W6V3YshzKOdqJIIfammjmFAeuA33S4SnR
MClajvPnz6tfHVo3+GpEwOpMfCQhJCSnt0dZkpKSYquYQ+Gofjgr3uOOHTvG
jBkjGmFq1KihsKSYQMFy+JLZIGxZDrwC9XMkHcGWQFFe8NT2Llqlw4OiQVjV
WGRnxErrxDF94NutlukoFNwzKNeW5UCxqL4db8+ePaK7UNp4+9RTT6m53arl
8D2zQVhaDreZDcKq5fCU2RColw6Pi4bJhuVwj9kgrFoOt5kNwqrlQF5WaTbG
jh3r7+9frFixFi1aTJ069bKZ6OjokJCQotaWoLHEquXwPbNBWFoOt5kNwlKm
PGs2BGqkA6Jx4MABz4oGIVNad5oNwtJyuM1sEJaWAwWiym0OoLFkMCZOnCg7
FR8fHxgYGBwcbGuJVykyywGzgeThe2aDkFoON5sNQmY5PG42BMrSQU7D1a2O
KpFZDneaDUJmOdxsNgiZ5VBpNvCsUD2Br9i+fbvVCE+fPr1IkSJquglklsNX
zQYhtRxuNhuEVKyQ8Ay1ca0t6TCUaBBCb91vNgip5XCz2SCklkO92di9ezec
xjfffGP1LF4xLS2osntRWA7fNhsEWQ6PmA1CWA7jmA2BpXQYUDRMEsuBB+hm
s0EIy+ERs0EIy6G+ZSMnJ8fWCqsQItoIRr1uCMvh22aDIMuBrOF+s0GQZCEa
hjIbAql0GFM0CKguXLdHzAZBlsMjZoMgy5GZmenIcGiTOUGuWLEiIiKCulRG
jhypXgYhWYiAz5sNIi4ujrbD81QEkNLgGI1mNgQkHUiNhhUNk9ly7NixwyNm
g4DlQLbds2ePR8wGAcuxa9curRsKT5s2beDAgT///PMeM2J2f0hIyOuvv64p
KFgOZCWfNxvEuXPnIB2e2iPAZN5xyfHVeFwKMsXx48cTEhJcOmraES5fvoya
gmf7d+DnUeA6ZYEUfZw5c0bNSC0ZsmVJaPWYMWPG6DBO1LLhyIQX7wLmylND
Ec6ePetZ1VIJFCM5ORn5QnlvRPeDiKWlpeEZGiFieJsoAjzyNlNTU/F2dLid
vXv3Pv7442J9queff153HApDy4YMj0iHt4iGAN4MT8mR1bCdCwr3+Pj4xMRE
D9YOZHhEOnSLhgCFQpcuXaAbNWvW1Ld2qK8OELWLm6XD60SDQB0WXlS6V7Kn
uH79OnIoagdGqz25WTocFw0CFZP+/fv7mfep17FGTSE0GwK3SYeXigZx+/bt
X3/9FYnEgxn28uXLkC+tbYBuw23S4SzREFSvXh2uQ3mzcksKrdkQuEE6vFo0
CKSTpKSk3377zf2tCqJBw7CdO4QbpMPpomEyr1EG6ShevHhkZKT6uwqz2RC4
VDp8QDQE+C1ubu4oKChISEgwVIOGAi6VDleIBkEbS3Xt2lXl9Ww2BC6SDl8S
DcKdzR3UoIFquNEaNBRwkXQ4UTSio6NlS+Ai5ZcqVapp06Yqe1TZbEhxunT4
nmgQ7mnuMHiDhgJOlw7nOo3SZqpUqfLSSy998MEHWWbeeOMNWA41o0HYbFji
ROnwVdEgXNrc4S0NGgo4UTqcXj3ZsWNHFzM0hEO6bo8a3WCzYRWnSIdvi4bA
Fc0dBhyhoQ+nSIfr2jRM5qSenp4+b968Xr16tWvX7uWXX7YbWzYbCjgoHYVE
NAjnNnd4Y4OGAg5Kh0tFwyp47HgFCrLAZkMZ3dJRqESDcFZzh/c2aCigWzrc
LxoEioDjx49bPcVmQw06pKMQigbhYHMHBAfZBI/OCOsQOh0d0uEp0TCZt2ix
NQ+azYZKNElHoRUNgb7mDp9p0FBAk3R4UDQIq5aDzYYmVEoHiwahtbkDtenY
2FifadBQQKV0eFw0TDYsB5sNrdiVDhYNKeqbO2ipKB9r0FDArnSkpaV5XDQI
meUoDCuIugIF6SDRMMJaEMbBbnOHbzdoKKAgHcYRDZOF5WCzoRur0sGioYCt
5o7C0KChgFXpMJRoEMJysNlwEJl0sGjYxbK5g5YiLwwNGgrIpMOAomGSWA42
G44jpINFQyXS5o7C1qChgJAOY4oGAcGHLWSz4RSysrJ27ty5d+9eFg2VwOgi
+UE9CmGDhgLIldu2bcMzMaZomMzNUD/99JOtYWCMVvCiUUagvECpYdiXbhBy
cnKQ8GJiYhISEvhZyUDRg9IctTlPR8QKEI0TJ054cKcJXwVVddhv5Ag8Xk/t
/mNY4DEuXLhw2Aw+GHCHKYPw119/oeaLAsjTEfkHqEChZExKSuIX5yIKCgrO
nDkTGxsbHx+P+js/Z9REUlJSIKewGTAbno6OFwDXgUyanJwMsfV0XP6HMaXM
J4Gp+/PPP48ePYoHnpGRUQibPvgJOAJVCn777TcPbiNIwByi6pSdne3ZaBQ2
CmFpy47LWVCe9VRzB2kX6pUe165CSyGp3XMLj9PxVB1BNGgYpK5UyBG9Camp
qT7TCU4jMbhHyUW4v7mDGzSMCVLCqVOnYEFR/b9y5Yr3DpXED0lPT/eBH2Jw
3Nnccf78eW7QMDJeXUwL45SWluYzxsnguLq5g9Tp119/5QYNr8CLmgUgbiiP
fL6hxrC4rgbBDRpeCnVDwHscOXLk8uXLRvP8omMIScs4+9EXQlzR3MENGt6O
0YY9GC0+jMnZzR3UoGHMwe2MVjxevsP/oACKjY01pv9hHG/u4AYNX8Uj7Qle
1N5SyHGkfsENGoUBN/RfeHX/TqFFX3MHN2gUKlw0XkIEm5iYmJ2dzVUS70Jr
cwc3aBROnGgMkHh4GIZvoKa5gxs0GJMDDRGQGpovgyR08eJFruH6Bsq1D2rQ
MM70fMazaOr4uHnzZmpqKg/D8FVsNXdwgwZjFeWBFnQ2ISGBh2H4PJbNHdyg
wdhF5ihQJSE3Eh8fn5WVxW2ehQRq7kBNlhs0GPWIgR/bt2/fv3//6dOnUZ3x
dKQYN4G3D3uZmJi4c+dObtBgdADLce7cuWPHjsGBQEZgReA6WEN8D4jDlStX
0tPTUUPZt28faqzwmbw3DeMgqKFcv34daQnFEBwIUhc0BOmKx3d5L3fv3s3O
zoZW/P7776QVMJa5ublcG2VcAdIVar5nzpwhDUGqS0tLQwpkDTE+0IqrV6+e
OnUqPj4e7y4hISEjIwOuktc0YNwJNASpDuUUUiDKLGgIyi+kTE6HxgHvKCcn
B/pAWoH/8RlH+B0xRoDSJzQEKRMacuTIEaRP1hCPgGdOek5agXdBes6NnIyR
IT8M3UCKpTIOaZjLOJdC3g/1x6NHjwrvh/ojawXjjZCGiPY31GigIUjh3P7m
ONTWJG2vTktLu3LlCmsF40sgPaMERNqGhiCdI7WjfETKZw1RD2nFuXPnSCuo
f5z7tphCAo0vQppHKUkagnLz+vXrrCFWwZM5f/48TUCGVqSkpODp8VgapjCD
9J+VlQUNQY5Avjh27BjK0xs3bng6Xh7m5s2b0IqkpCQ8k7i4uJMnT+Ip5efn
ezpeDGM4kC8uX76M8hQ5hfbGvXDhQuHRkFu3buH3JicnHzhw4NChQydOnMjM
zOS5hAyjHuQXaAjyDnIQ8hFKXuQplMKejpeTgVZcvHjxjz/+OHjwYGxsLD5c
unSJZ5MxjOMgH6HkRZ6ChiB/4QPymqHWGYMpmjBhwssvv1ynTp3KlSsXLVo0
IiLC1qaH+DkQB/yKWDMwGKwVDONSKNMhr1GmM0IBffXq1U6dOvn5+RWVgD8r
VKjw0ksv/fLLL9L+jpycHNgnxB/2yVDSxzCFBIM0CDz99NMkFDLdEJ+XLFki
LuY+U4YxDp7qgIiPjw8ICFDWjSpVqkycONHVMWEYxhHcOeABX+FnpkiRIvRh
6NChZcqUEX8SgYGB0DRXRIBhGOciG2D566+/OmuAJS13Q8ujNW3aNDQ0dODA
gTJl2LJly4cfflivXj2yH6+88oqDX8owjJsREzqOHj1KEzrS09M1TeigofLS
5W7U6A+uL1euHHSjRYsWjv0ChmE8CTQkNzf39OnTsgmklpN2SStOnTpF02po
eq+m5W4uXrxYvnx51g2G8SVowYqMjIyEhARSBqgEHZEud6M8jTc6OnrkyJFQ
hmeeeebAgQPSUz169KB6CusGw/gk0BBaIGv37t0nT55UufRQVFRUsWLFRENo
6dKlQ0NDDx8+TKeqVq1KraYQFtf/AoZhPAZ1x6i8+KuvvlLuh6WuWO5PYRjf
Bjbj4MGDKqfUpaent2/fXkE3evXqpV6FGIbxXjRZDvD9998/cZ+GDRtKdWPC
hAmuiyfDMMZBk+WQcfnyZdzbu3dvrqQwTGFDq+WQceHChbCwMGosrVOnjhMj
xjCMYdFkOTIzM1EfWbJkSW5urjiYkZFRrVo1WI4yZcr8/vvvLospwzAGQr3l
ePvtt6lWUq9evZdeeuno0aOJiYnXrl2bNGkSNZPOnz/f1bFlGMYIqLccR44c
IWsh7U9p06ZNs2bN6M8ZM2a4IcIMwxgB9ZbjzJkz7733XocOHSzHb1SsWPHq
1auujirDMAZBa8dKXl7egQMHlixZMmTIkB49ejxtZu3atS6NJMMwRkPZcty7
d+/69eu8kSXDMFKULUdGRsbJkyc1BYig9u7d+62ZxMRE3pyRYXwSW5bjzp07
MTExmhZG3rRp04MPPviAhNatWy9dutR5kWUYxhDYshxazUZBQUFISEiNGjXm
zZsXGRnZt29fko6iRYuOGjXq2rVrTo01wzAextJy6DAbICkpSYwNu3Xr1o4d
OwYOHEjqMWDAAKdFl2EYA2BpOXS0bNgKmaQDPiQ9Pd3xABmGMQ5Sy6HPbNgi
KysrNDQU0hEREeGUABmGMQhSy6HGbGRnZ4eHh9euXXvWrFl2FWbKlClUW3Fa
dBmGMQZkOVSajZSUFNFp0rhx40GDBg0ePHivGYQju3jcuHGsGwzjk5DlOHHi
hJqWjdTUVD8/vwesUaVKlcb/pESJEjjetGlTN/wKhmHczNmzZ7dt26ZyE8nn
n3+ehKJkyZL/+c9/WrVqZVVGiEcffRQ2xtXxZxjG/WiasZKdnR0cHEyy8Nhj
j129enXLli3DrbFgwYI///zT1ZFnGMZTaFoKLCcnB7UPko5SpUrhT5fGjWEY
Y6J1kuyxY8fCw8OF64AJcWn0GIYxJlpXH929e3dAQABJx5w5cxR2f2MYxlfR
seD5li1bAgMDSTo2bdrkurgxDGNYFCzHrVu3rB7ftm0b6cbQoUNdGTWGYQyK
guWYMWNG//79hw8fvtNMfHz8OTP5+fmkG0FBQbypCsMUTmxZjs8++6xo0aJF
ihQhlQgICKhkRrryxt69e90fYYZhPI6C5Zg/f36LFi1sDfFq2bJlZmam+yPM
MIwRUGjlyMvLQw3lzTfffO2115YuXbp27dpJkya99957OJiVleXmeDIMYxzs
dqzcu3fv77//5o5XhmGkKI/lyM3NPXv2rDvjwzCM8VGwHLAZcXFxPLacYRhL
bFmOzMzM+Ph498eHYRjjY9VysNlgGEYZS8vBZoNhGGVkloPNBsMwapBaDjYb
DMOoQVgONhsMw6iHLAebDYZh1APLceDAgZiYGDYbDMOo58KFC8eOHfN0LBiG
YRiGYRiGYRiGYRiGYRiGYRiGYRhGLf8PSl6oKg==
"], {{0, 0}, {360, 258}}, {0,
255},
ColorFunction->RGBColor],
ImageSize->{360, 258},
PlotRange->{{0, 360}, {0, 258}}]\)