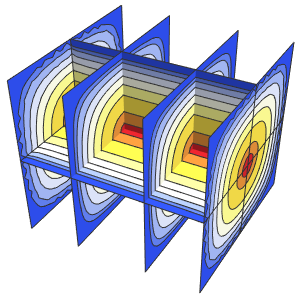
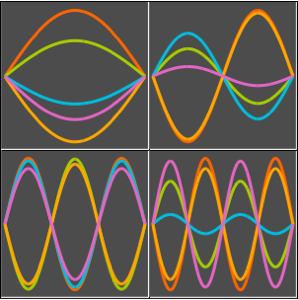
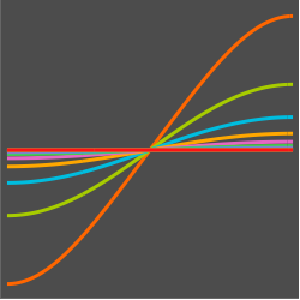
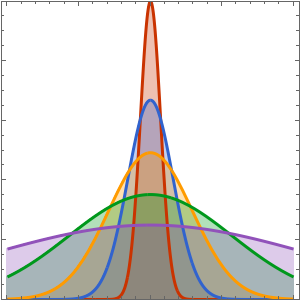
求解拉普拉斯方程的狄利克雷问题

指定二维拉普拉斯（Laplace）方程.

In[1]:=

leqn = Laplacian[u[x, y], {x, y}] == 0;

在矩形中规定方程的狄利克雷（Dirichlet）条件.

In[2]:=

\[CapitalOmega] = Rectangle[{0, 0}, {1, 2}];

In[3]:=

dcond = DirichletCondition[ u[x, y] == Piecewise[{{UnitTriangle[2 x - 1], y == 0 || y == 2}}, 0], True];

求解狄利克雷问题.

In[4]:=

sol = DSolveValue[{leqn, dcond}, u[x, y], {x, y} \[Element] \[CapitalOmega]] // FullSimplify

Out[4]=

从 Inactive 总和中提取前 300 项.

In[5]:=

asol = sol /. {\[Infinity] -> 300} // Activate;

在矩形上可视化方程的解.

In[6]:=

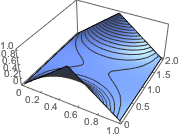
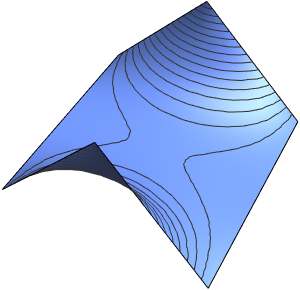
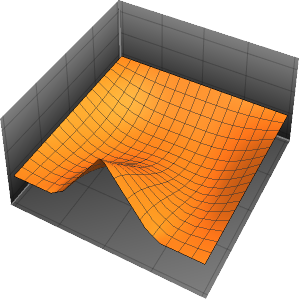
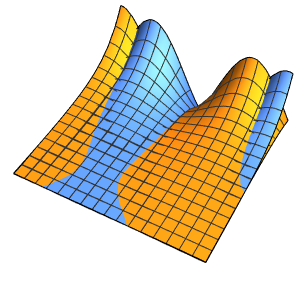
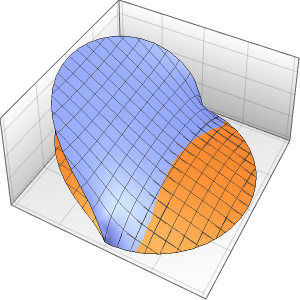
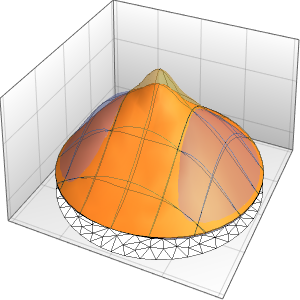
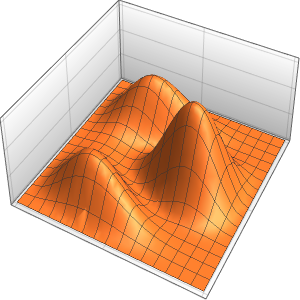
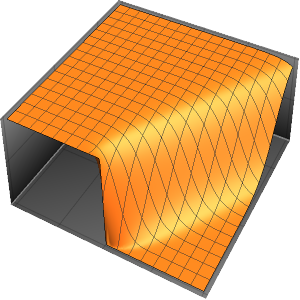
Plot3D[asol // Evaluate, {x, y} \[Element] \[CapitalOmega], PlotRange -> All, PlotTheme -> "Business"]

Out[6]=