Solve a Poisson Equation with Periodic Boundary Conditions
Solve a Poisson equation with periodic boundary conditions on curved boundaries.
Specify a region.
In[1]:=
\[CapitalOmega] =
RegionDifference[RegionUnion[Disk[], Rectangle[{0, -1}, {2, 1}]],
Disk[{2, 0}]];Solve the partial differential equation with periodic boundary conditions where the solution from the left-hand side is mapped to the right-hand side of the region.
In[2]:=

ufun = NDSolveValue[{-\!\(
\*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[x, y]\)\) == 1,
PeriodicBoundaryCondition[u[x, y], (x - 2)^2 + y^2 == 1,
Function[x, x - {2, 0}]],
DirichletCondition[
u[x, y] == 0, (0 <= x < 2 - 10^-6 && (y <= -1 || y >= 1))]},
u, {x, y} \[Element] \[CapitalOmega]];Visualize the solution.
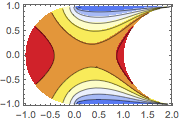
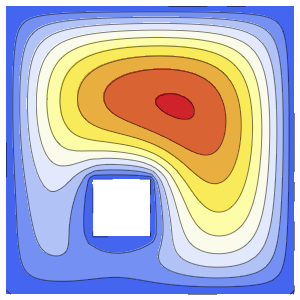
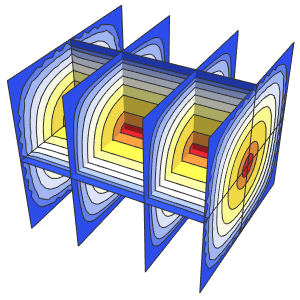
In[3]:=
ContourPlot[ufun[x, y], {x, y} \[Element] \[CapitalOmega],
ColorFunction -> "TemperatureMap", AspectRatio -> Automatic]Out[3]=