Construct a Complex Analytic Function
Construct a complex analytic function, starting from the values of its real and imaginary parts on the  axis.
axis.
The real and imaginary parts u and v satisfy the Cauchy–Riemann equations.
In[1]:=
creqns = {D[u[x, y], x] == D[v[x, y], y],
D[v[x, y], x] == -D[u[x, y], y]};Prescribe the values of u and v on the  axis.
axis.
In[2]:=
xvals = {u[x, 0] == x^3, v[x, 0] == 0};Solve the Cauchy–Riemann equations.
In[3]:=
sol = DSolve[{creqns, xvals}, {u, v}, {x, y}]Out[3]=
Verify that the solutions are harmonic functions.
In[4]:=
Laplacian[{u[x, y], v[x, y]} /. sol[[1]], {x, y}]Out[4]=
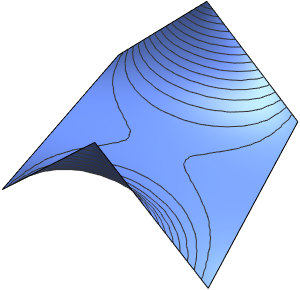
Visualize the streamlines and equipotentials generated by the solution.
In[5]:=
ContourPlot[{u[x, y], v[x, y]} /. sol[[1]], {x, -5, 5}, {y, -5, 5},
ContourStyle -> {Red, Blue}]Out[5]=
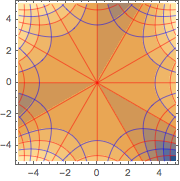
Construct a complex analytic function from the solution.
In[6]:=
f[x_, y_] = u[x, y] + I v[x, y] /. sol[[1]]Out[6]=
This represents the function  .
.
In[7]:=
(f[x, y] // Factor) /. {x + I y -> z}Out[7]=