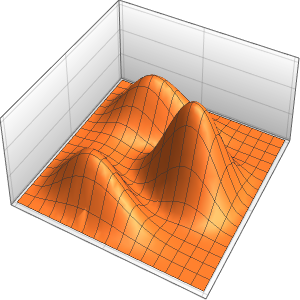
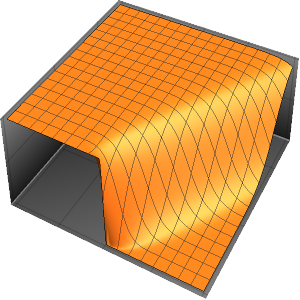
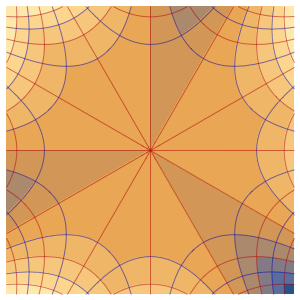
量子力学における分散を調べる
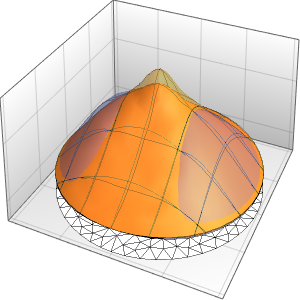
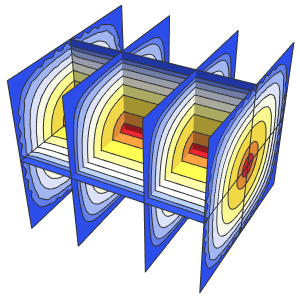
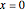の周りに強く局在している1つの自由粒子について一次元のシュレディンガー（Schrödinger）方程式を解く．
In[1]:=
eqn = I D[\[Psi][x, t], t] == D[\[Psi][x, t], {x, 2}];
sol[x_, t_] =
DSolveValue[{eqn, \[Psi][x, 0] == Exp[-x^2]}, \[Psi][x, t], {x, t}]Out[1]=
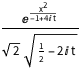
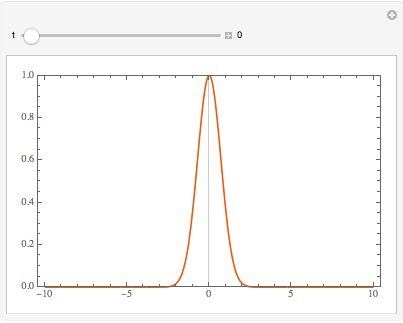
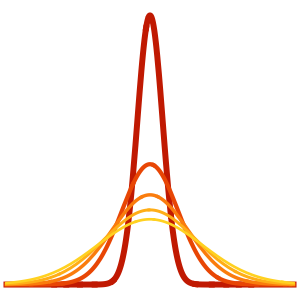
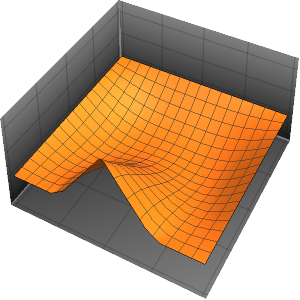
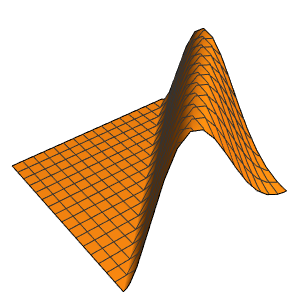
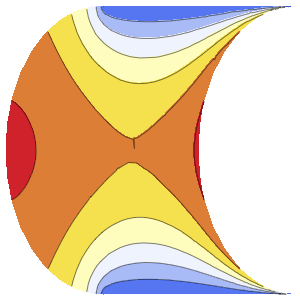
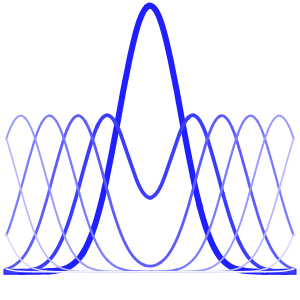
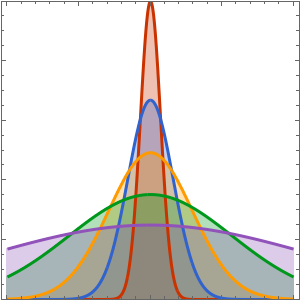
時間が経つにつれて，波動関数の原点におけるピークはそれほど顕著ではなくなる．
In[2]:=
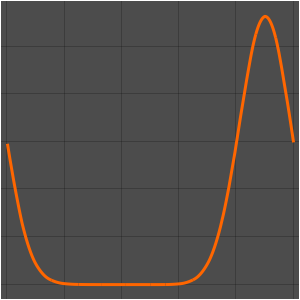
Manipulate[
Plot[Abs@sol[x, t], {x, -10, 10}, PlotRange -> {0, 1},
PlotTheme -> "Scientific", ImageSize -> Medium], {t, 0, 5,
Appearance -> "Labeled"}]
