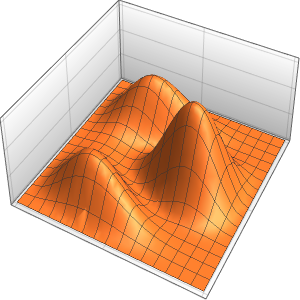
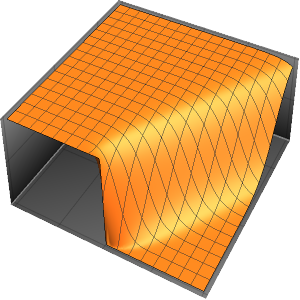
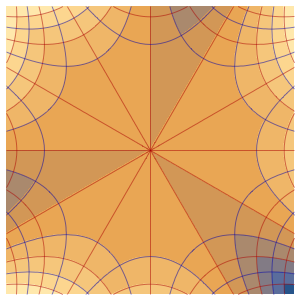
研究弦线的震动
使用波动方程研究弦线的震动.
In[1]:=
weqn = D[u[x, t], {t, 2}] == D[u[x, t], {x, 2}]; 假定在震动过程中,弦线的两端保持固定.
In[2]:=
bc = {u[0, t] == 0, u[\[Pi], t] == 0};给出弦上不同点的初始值.
In[3]:=
ic = {u[x, 0] == x^2 (\[Pi] - x),
\!\(\*SuperscriptBox[\(u\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, 0] == 0};求解初边值问题.
In[4]:=
dsol = DSolve[{weqn, bc, ic}, u, {x, t}] /. {K[1] -> m}Out[4]=
从 Inactive 总和中提取四项.
In[5]:=
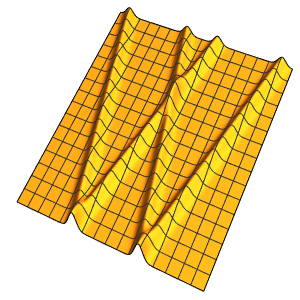
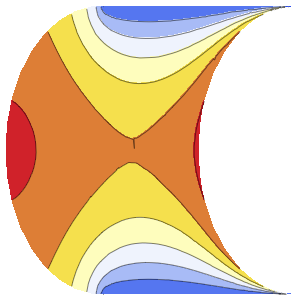
asol[x_, t_] = u[x, t] /. dsol[[1]] /. {\[Infinity] -> 4} // ActivateOut[5]=
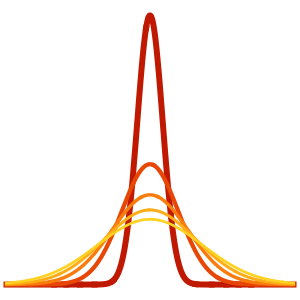
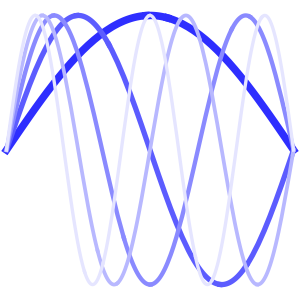
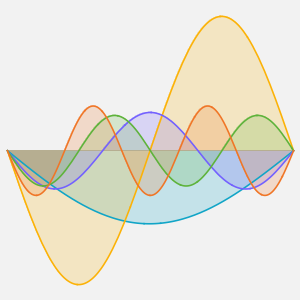
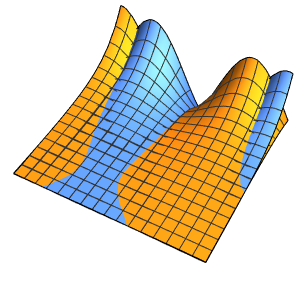
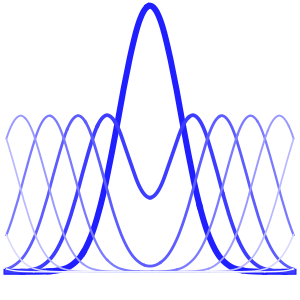
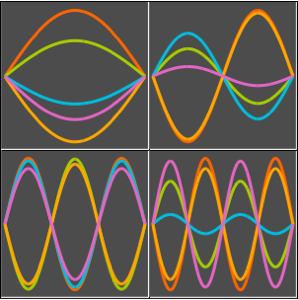
总和中的每个项代表一个驻波(standing wave).
In[6]:=
Table[Show[
Plot[Table[asol[x, t][[m]], {t, 0, 4}] // Evaluate, {x, 0, Pi},
Ticks -> False], ImageSize -> 150], {m, 4}]Out[6]=

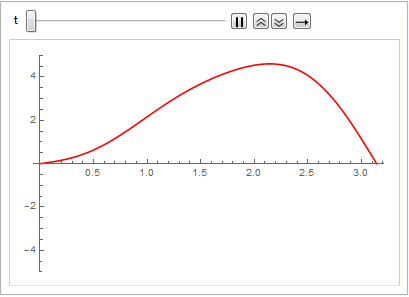
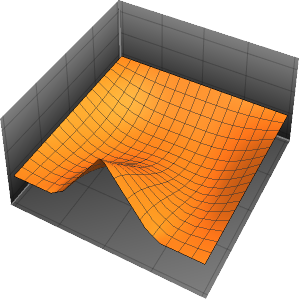
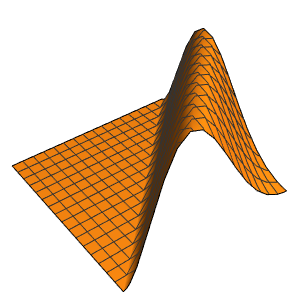
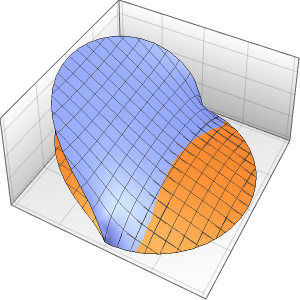
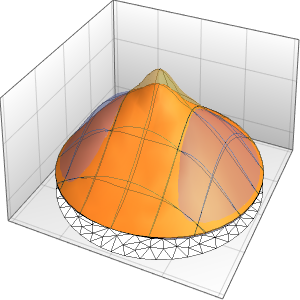
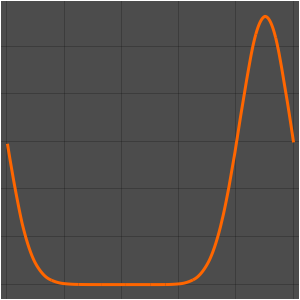
可视化弦的震动.
In[7]:=
Animate[Plot[asol[x, t], {x, 0, \[Pi]}, PlotRange -> {-5, 5},
ImageSize -> Medium, PlotStyle -> Red], {t, 0, 2 Pi},
SaveDefinitions -> True]