Travel Planning

The average speed of cars traveling from Indianapolis, Indiana, to Chicago, Illinois, is described by a TriangularDistribution.

In[1]:=

speed\[ScriptCapitalD] = TriangularDistribution[{\!\(\* NamespaceBox["LinguisticAssistant", DynamicModuleBox[{Typeset`query$$ = "55 mi/h", Typeset`boxes$$ = TemplateBox[{"55", RowBox[{"\"mi\"", " ", "\"/\"", " ", "\"h\""}], "miles per hour", FractionBox["\"Miles\"", "\"Hours\""]}, "Quantity", SyntaxForm -> Mod], Typeset`allassumptions$$ = {}, Typeset`assumptions$$ = {}, Typeset`open$$ = {1, 2}, Typeset`querystate$$ = { "Online" -> True, "Allowed" -> True, "mparse.jsp" -> 3.9373779`8.046752092819743, "Messages" -> {}}}, DynamicBox[ToBoxes[ AlphaIntegration`LinguisticAssistantBoxes["45", 4, Automatic, Dynamic[Typeset`query$$], Dynamic[Typeset`boxes$$], Dynamic[Typeset`allassumptions$$], Dynamic[Typeset`assumptions$$], Dynamic[Typeset`open$$], Dynamic[Typeset`querystate$$]], StandardForm], ImageSizeCache->{94., {8., 16.}}, TrackedSymbols:>{ Typeset`query$$, Typeset`boxes$$, Typeset`allassumptions$$, Typeset`assumptions$$, Typeset`open$$, Typeset`querystate$$}], DynamicModuleValues:>{}, UndoTrackedVariables:>{Typeset`open$$}], BaseStyle->{"Deploy"}, DeleteWithContents->True, Editable->False, SelectWithContents->True]\), \!\(\* NamespaceBox["LinguisticAssistant", DynamicModuleBox[{Typeset`query$$ = "82 mph", Typeset`boxes$$ = TemplateBox[{"82", RowBox[{"\"mi\"", " ", "\"/\"", " ", "\"h\""}], "miles per hour", FractionBox["\"Miles\"", "\"Hours\""]}, "Quantity", SyntaxForm -> Mod], Typeset`allassumptions$$ = {}, Typeset`assumptions$$ = {}, Typeset`open$$ = {1, 2}, Typeset`querystate$$ = { "Online" -> True, "Allowed" -> True, "mparse.jsp" -> 0.2656176`6.875801841788495, "Messages" -> {}}}, DynamicBox[ToBoxes[ AlphaIntegration`LinguisticAssistantBoxes["", 4, Automatic, Dynamic[Typeset`query$$], Dynamic[Typeset`boxes$$], Dynamic[Typeset`allassumptions$$], Dynamic[Typeset`assumptions$$], Dynamic[Typeset`open$$], Dynamic[Typeset`querystate$$]], StandardForm], ImageSizeCache->{94., {8., 16.}}, TrackedSymbols:>{ Typeset`query$$, Typeset`boxes$$, Typeset`allassumptions$$, Typeset`assumptions$$, Typeset`open$$, Typeset`querystate$$}], DynamicModuleValues:>{}, UndoTrackedVariables:>{Typeset`open$$}], BaseStyle->{"Deploy"}, DeleteWithContents->True, Editable->False, SelectWithContents->True]\)}, \!\(\* NamespaceBox["LinguisticAssistant", DynamicModuleBox[{Typeset`query$$ = "72 mph", Typeset`boxes$$ = TemplateBox[{"72", RowBox[{"\"mi\"", " ", "\"/\"", " ", "\"h\""}], "miles per hour", FractionBox["\"Miles\"", "\"Hours\""]}, "Quantity", SyntaxForm -> Mod], Typeset`allassumptions$$ = {}, Typeset`assumptions$$ = {}, Typeset`open$$ = {1, 2}, Typeset`querystate$$ = { "Online" -> True, "Allowed" -> True, "mparse.jsp" -> 0.250013`6.8495075848939235, "Messages" -> {}}}, DynamicBox[ToBoxes[ AlphaIntegration`LinguisticAssistantBoxes["", 4, Automatic, Dynamic[Typeset`query$$], Dynamic[Typeset`boxes$$], Dynamic[Typeset`allassumptions$$], Dynamic[Typeset`assumptions$$], Dynamic[Typeset`open$$], Dynamic[Typeset`querystate$$]], StandardForm], ImageSizeCache->{94., {8., 16.}}, TrackedSymbols:>{ Typeset`query$$, Typeset`boxes$$, Typeset`allassumptions$$, Typeset`assumptions$$, Typeset`open$$, Typeset`querystate$$}], DynamicModuleValues:>{}, UndoTrackedVariables:>{Typeset`open$$}], BaseStyle->{"Deploy"}, DeleteWithContents->True, Editable->False, SelectWithContents->True]\)]

Out[1]=

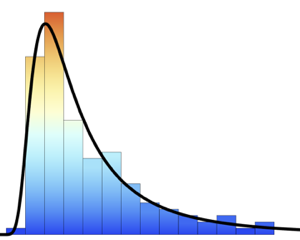
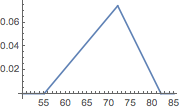
The probability density function for the speed distribution.

In[2]:=

Plot[PDF[speed\[ScriptCapitalD], Quantity[x, "mph"]], {x, 50, 85}]

Out[2]=

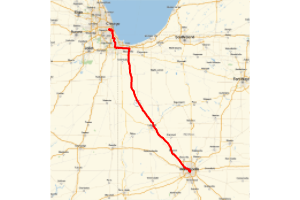
Calculate the distance between the cities, assuming driving.

In[3]:=

GeoGraphics[ Style[Line[ TravelDirections[{Entity[ "City", {"Indianapolis", "Indiana", "UnitedStates"}], Entity["City", {"Chicago", "Illinois", "UnitedStates"}]}]], Thick, Red], GeoBackground -> GeoStyling["StreetMap"], GeoRange -> Quantity[100, "Miles"]]

Out[3]=

In[4]:=

distance = TravelDistance[{Entity[ "City", {"Indianapolis", "Indiana", "UnitedStates"}], Entity["City", {"Chicago", "Illinois", "UnitedStates"}]}, TravelMethod -> "Driving"]

Out[4]=

Find the expected time of travel.

In[5]:=

Expectation[distance/v, v \[Distributed] speed\[ScriptCapitalD]]

Out[5]=

Convert to hours and minutes.

In[6]:=

Expectation[distance/v, v \[Distributed] speed\[ScriptCapitalD]]; UnitConvert[%, MixedUnit[{"Hours", "Minutes"}]]

Out[6]=

Assuming gas mileage as a function of car speed is given by the following interpolating function, the expected amount of gas needed for the trip can be calculated using NExpectation.

In[7]:=

mpg = Interpolation[{Quantity[{40, 50, 60, 70, 80}, "miles per hour"], Quantity[{33, 32, 28, 25, 20}, "miles per gallon"]} // Transpose, InterpolationOrder -> 1];

In[8]:=

NExpectation[distance/mpg[v], v \[Distributed] speed\[ScriptCapitalD]]

Out[8]=