Truncated Distribution with Quantities
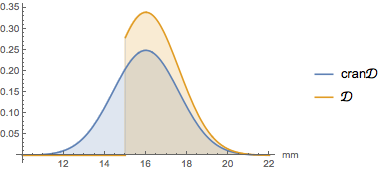
The diameter of an American cranberry follows a normal distribution with mean 16 mm and standard deviation 1.6 mm. A fruit must be at least 15 mm across to be sold as whole; otherwise, it is used in the production of cranberry sauce. Find the size distribution of the fruits being sold as whole.
In[1]:=
cran\[ScriptCapitalD] =
NormalDistribution[Quantity[16, "Millimeters"],
Quantity[1.6, "Millimeters"]];
\[ScriptCapitalD] =
TruncatedDistribution[{Quantity[15, "Millimeters"], \[Infinity]},
cran\[ScriptCapitalD]];Compare probability density functions.
In[2]:=

Plot[{PDF[cran\[ScriptCapitalD], Quantity[x, "Milimeters"]],
PDF[\[ScriptCapitalD], Quantity[x, "Milimeters"]]}, {x, 10, 22},
PlotLegends -> {"cran\[ScriptCapitalD]", "\[ScriptCapitalD]"},
Filling -> Axis, AxesLabel -> {"mm"}]Out[2]=
Assuming that a one-pound package of cranberries has volume around 30 in3, find the average lower and upper bounds for the number of cranberries in such a package.
In[3]:=

lowerbound =
Floor[NExpectation[
Divide[Quantity[30, "Inches"^3],
Volume[Cuboid[{0, 0, 0}, {x, x, x}]]],
x \[Distributed] \[ScriptCapitalD]]]Out[3]=
In[4]:=

upperbound =
Ceiling[NExpectation[
Divide[Quantity[30, "Inches"^3], Volume[Ball[{0, 0, 0}, x/2]]],
x \[Distributed] \[ScriptCapitalD]]]Out[4]=