信号導関数を近似する
MovingMapを使って,不規則にサンプルされた連続時系列からの信号の導関数を近似する.
In[1]:=
ts = TimeSeries[
Table[{t, EllipticTheta[1, t, 0.3]}, {t,
Join[{0.}, RandomReal[{0, 2 Pi}, 254], {2. Pi}]}]]Out[1]=
In[2]:=
RegularlySampledQ[ts]Out[2]=
In[3]:=
ListPlot[ts, PlotTheme -> "Detailed"]Out[3]=
各移動窓の境界における値と時間を使って,差分商を計算する.
In[4]:=
quotient[values_, times_] :=
First[Differences[values]/Differences[times]]In[5]:=
mm = MovingMap[quotient[#BoundaryValues, #BoundaryTimes] &,
ts, {.01, Right}]Out[5]=
理論上の導関数と比較する.
In[6]:=
prime = D[EllipticTheta[1, t, 0.3], t]Out[6]=
In[7]:=
Show[Plot[prime, {t, 0, 2 \[Pi]}, PlotStyle -> Thick,
PlotTheme -> "Detailed", PlotLegends -> None],
ListPlot[mm, PlotStyle -> Red]]Out[7]=
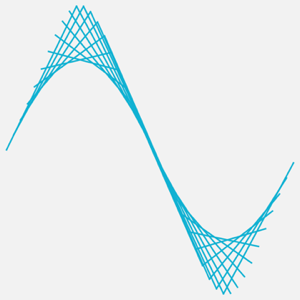
商関数の代りにLineを使ったMovingMapで,もとの時系列を近似する割線のプロットを生成する.
In[8]:=
line[yvals_, xvals_] := Line[Transpose[{xvals, yvals}]];In[9]:=
lines = MovingMap[ line[#BoundaryValues, #BoundaryTimes] &,
ts, {1.3, Right, {0, 2. \[Pi], .1}}];In[10]:=
Graphics[{Black, lines["Values"]}]Out[10]=